Left Endpoint, Right Endpoint and Midpoint Rules
There are two possible situation when we need numerical approximation (rule):
- To calculate $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}$$$ we need to know antiderivative of $$${f{{\left({x}\right)}}}$$$. In some cases, it is difficult, or even impossible to find an antiderivative. For example, $$${\int_{{1}}^{{3}}}\frac{{{\sin{{\left({x}\right)}}}}}{{x}}{d}{x}$$$ and $$${\int_{{1}}^{{2}}}\sqrt{{{{u}}^{{3}}+{1}}}{d}{u}$$$ can't be found exactly.
- The function is determined from a scientific experiment through instrument readings or collected data. There may be no formula for the function.
Actually we already made approximations when we introduced Definite Integral. We approximated area under curve by dividing interval into $$${n}$$$ subintervals, where i-th subinterval is $$${\left[{x}_{{{i}-{1}}},{x}_{{i}}\right]}$$$ and calculate sum of areas of $$${n}$$$ rectangles. Then we said that when $$${n}\to\infty$$$ then sum of areas of those rectangles is $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}$$$ :
$$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}=\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{f{{\left({{x}_{{i}}^{{\star}}}\right)}}}\Delta{x}$$$, where $$$\Delta{x}=\frac{{{b}-{a}}}{{n}}$$$ and $$${{x}_{{i}}^{{\star}}}$$$ lies in interval $$${\left[{x}_{{{i}-{1}}},{x}_{{i}}\right]}$$$.
This gives us ability to approximate definite integral: $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}\approx{\sum_{{{i}={1}}}^{{n}}}{f{{\left({{x}_{{i}}^{{\star}}}\right)}}}\Delta{x}$$$.
If we choose $$${{x}_{{i}}^{{\star}}}$$$ to be left endpoint $$${x}_{{{i}-{1}}}$$$ of interval $$${\left[{x}_{{{i}-{1}}},{x}_{{i}}\right]}$$$ then this approximation is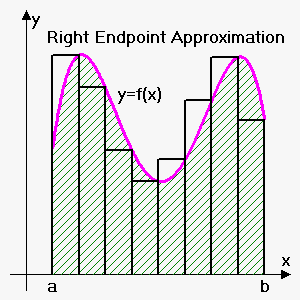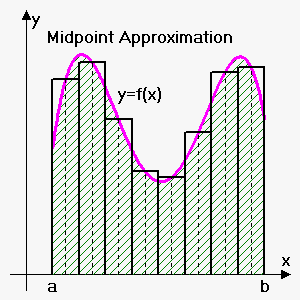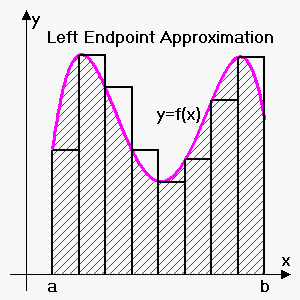 
called Left Endpoint Approximation: $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}\approx{L}_{{n}}={\sum_{{{i}={1}}}^{{{n}}}}{f{{\left({x}_{{{i}-{1}}}\right)}}}\Delta{x}$$$.
If we choose $$${{x}_{{i}}^{{\star}}}$$$ to be right endpoint $$${x}_{{i}}$$$ of interval $$${\left[{x}_{{{i}-{1}}},{x}_{{i}}\right]}$$$ then this approximation is called Right Endpoint Approximation: $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}\approx{R}_{{n}}={\sum_{{{i}={1}}}^{{{n}}}}{f{{\left({x}_{{i}}\right)}}}\Delta{x}$$$.
If we choose $$${{x}_{{i}}^{{\star}}}$$$ to be midpoint of interval $$${\left[{x}_{{{i}-{1}}},{x}_{{i}}\right]}$$$, i.e. $$${{x}_{{i}}^{{\star}}}=\frac{{1}}{{2}}{\left({x}_{{{i}-{1}}}+{x}_{{i}}\right)}$$$ then this approximation is called Midpoint Rule Approximation: $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}\approx{M}_{{n}}={\sum_{{{i}={1}}}^{{{n}}}}{f{{\left(\frac{{1}}{{2}}{\left({x}_{{{i}-{1}}}+{x}_{{i}}\right)}\right)}}}\Delta{x}$$$.
Example. Approximate $$${I}={\int_{{1}}^{{2}}}\frac{{1}}{{{x}}^{{2}}}{d}{x}$$$ using above three methods with $$${n}={5}$$$.
We have $$${f{{\left({x}\right)}}}=\frac{{1}}{{x}}$$$, $$${a}={1}$$$, $$${b}={2}$$$, $$${n}={5}$$$, so $$$\Delta{x}=\frac{{{b}-{a}}}{{n}}=\frac{{{2}-{1}}}{{5}}={0.2}$$$.
Interval is divided into $$${n}={5}$$$ subintervals: $$${\left[{1},{1.2}\right]}$$$, $$${\left[{1.2},{1.4}\right]}$$$, $$${\left[{1.4},{1.6}\right]}$$$, $$${\left[{1.6},{1.8}\right]}$$$ and $$${\left[{1.8},{2}\right]}$$$.
Left endpoint approximation gives (left endpoints of intervals are 1, 1.2, 1.4, 1.6, 1.8)
$$${I}\approx{L}_{{n}}=\Delta{x}{\left({f{{\left({1}\right)}}}+{f{{\left({1.2}\right)}}}+{f{{\left({1.4}\right)}}}+{f{{\left({1.6}\right)}}}+{f{{\left({1.8}\right)}}}\right)}=$$$
$$$={0.2}{\left(\frac{{1}}{{{\left({1}\right)}}^{{2}}}+\frac{{1}}{{{\left({1.2}\right)}}^{{2}}}+\frac{{1}}{{{\left({1.4}\right)}}^{{2}}}+\frac{{1}}{{{\left({1.6}\right)}}^{{2}}}+\frac{{1}}{{{\left({1.8}\right)}}^{{2}}}\right)}\approx{0.580783}$$$.
Right endpoint approximation gives (right endpoints of intervals are 1.2, 1.4, 1.6, 1.8, 2)
$$${I}\approx{R}_{{n}}=\Delta{x}{\left({f{{\left({1.2}\right)}}}+{f{{\left({1.4}\right)}}}+{f{{\left({1.6}\right)}}}+{f{{\left({1.8}\right)}}}+{f{{\left({2}\right)}}}\right)}=$$$
$$$={0.2}{\left(\frac{{1}}{{{\left({1.2}\right)}}^{{2}}}+\frac{{1}}{{{\left({1.4}\right)}}^{{2}}}+\frac{{1}}{{{\left({1.6}\right)}}^{{2}}}+\frac{{1}}{{{\left({1.8}\right)}}^{{2}}}+\frac{{1}}{{{2}}^{{2}}}\right)}\approx{0.430783}$$$.
Midpoint approximation gives
$$${I}\approx{M}_{{n}}=$$$
$$$=\Delta{x}{\left({f{{\left(\frac{{1}}{{2}}{\left({1}+{1.2}\right)}\right)}}}+{f{{\left(\frac{{1}}{{2}}{\left({1.2}+{1.4}\right)}\right)}}}+{f{{\left(\frac{{1}}{{2}}{\left({1.4}+{1.6}\right)}\right)}}}+{f{{\left(\frac{{1}}{{2}}{\left({1.6}+{1.8}\right)}\right)}}}+{f{{\left(\frac{{1}}{{2}}{\left({1.8}+{2}\right)}\right)}}}\right)}=$$$
$$$={0.2}{\left({f{{\left({1.1}\right)}}}+{f{{\left({1.3}\right)}}}+{f{{\left({1.5}\right)}}}+{f{{\left({1.7}\right)}}}+{f{{\left({1.9}\right)}}}\right)}={0.2}{\left(\frac{{1}}{{{\left({1.1}\right)}}^{{2}}}+\frac{{1}}{{{\left({1.3}\right)}}^{{2}}}+\frac{{1}}{{{\left({1.5}\right)}}^{{2}}}+\frac{{1}}{{{\left({1.7}\right)}}^{{2}}}+\frac{{1}}{{{\left({1.9}\right)}}^{{2}}}\right)}\approx$$$
$$$\approx{0.497127}$$$.
We deliberately chose integral that can be integrated directly to compare true value with approximations.
True value of integral is $$${I}={\int_{{1}}^{{2}}}\frac{{1}}{{{x}}^{{2}}}{d}{x}=-\frac{{1}}{{x}}{{\mid}_{{1}}^{{2}}}=-{\left(\frac{{1}}{{2}}-\frac{{1}}{{1}}\right)}=\frac{{1}}{{2}}={0.5}$$$.
As can be seen midpoint rule gave better approximation then endpoint approximations.
We will get more accurate approximations when we increase the value of $$${n}$$$. (But very large values result in so many arithmetic operations that we have to beware of accumulated round-off error).
As can be seen errors in the left and right endpoint approximations are opposite in sign.
Also, left endpoint approximation overestimated integral, while two other approximations underestimated it.
In general,
- if function $$${f{{\left({x}\right)}}}$$$ is increasing then left endpoint approximation underestimates value of integral, while right endpoint approximation overestimates it.
- If function $$${f{{\left({x}\right)}}}$$$ is decreasing then left endpoint approximation overestimates value of integral, while right endpoint approximation underestimates it.
- If function $$${f{{\left({x}\right)}}}$$$ is concave up then midpoint rule underestimates value of integral, if function $$${f{{\left({x}\right)}}}$$$ is concave down then midpoint rule overestimates value of integral.
When we approximate integral we will always have some error: $$${E}={\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}-{A}{p}{p}$$$ where $$${A}{p}{p}$$$ is approximation and $$${E}$$$ is error.
Error Bound for Midpoint Rule. Suppose $$${\left|{f{''}}{\left({x}\right)}\right|}\le{M}$$$ for $$${a}\le{x}\le{b}$$$ then $$${\left|{E}\right|}\le\frac{{{M}{{\left({b}-{a}\right)}}^{{3}}}}{{{24}{{n}}^{{2}}}}$$$.
Example. How large should we take $$${n}$$$ in order to guarantee that the Midpoint Rule approximation for $$${\int_{{1}}^{{2}}}\frac{{1}}{{{x}}^{{2}}}{d}{x}$$$ is accurate to within 0.0002?
Here $$${a}={1}$$$, $$${b}={2}$$$, $$${f{{\left({x}\right)}}}=\frac{{1}}{{{x}}^{{2}}}$$$.
Then $$${f{'}}{\left({x}\right)}=-\frac{{2}}{{{x}}^{{3}}}$$$ and $$${f{''}}{\left({x}\right)}=\frac{{6}}{{{x}}^{{4}}}$$$.
Therefore $$${\left|{f{''}}{\left({x}\right)}\right|}\le{6}$$$ for $$${1}\le{x}\le{2}$$$.
Thus, $$$\frac{{{6}{{\left({2}-{1}\right)}}^{{3}}}}{{{24}{{n}}^{{2}}}}<{0.0002}$$$ or $$${{n}}^{{2}}>\frac{{1}}{{{0.0008}}}$$$.
So, $$${n}>\frac{{1}}{\sqrt{{{0.0008}}}}\approx{35.36}$$$.
Therefore, we should take $$${n}={36}$$$ (the closest integer that is greater than 35.36).