Increasing and Decreasing Functions

A function ${f{}}$ is called increasing on interval ${I}$ if ${f{{\left({x}_{{1}}\right)}}}<{f{{\left({x}_{{2}}\right)}}}$ whenever ${x}_{{1}}<{x}_{{2}}$ in ${I}$.

A function ${f{}}$ is called decreasing on interval ${I}$ if ${f{{\left({x}_{{1}}\right)}}}>{f{{\left({x}_{{2}}\right)}}}$ whenever ${x}_{{1}}>{x}_{{2}}$ in ${I}$.

A function ${f{}}$ is called non-decreasing on interval ${I}$ if ${f{{\left({x}_{{1}}\right)}}}\le{f{{\left({x}_{{2}}\right)}}}$ whenever ${x}_{{1}}<{x}_{{2}}$ in ${I}$.

A function ${f{}}$ is called non-icreasing on interval ${I}$ if ${f{{\left({x}_{{1}}\right)}}}>{f{{\left({x}_{{2}}\right)}}}$ whenever ${x}_{{1}}>{x}_{{2}}$ in ${I}$.

All above types of functions have common name. They are called monotonic.

It is important to understand that in definition of increasing ${f{{\left({x}_{{1}}\right)}}}<{f{{\left({x}_{{2}}\right)}}}$ should hold for any ${x}_{{1}}$ and ${x}_{{2}}$ such that ${x}_{{1}}<{x}_{{2}}$. Same can be said about definition of decreasing, non-decreasing and non-increasing functions.

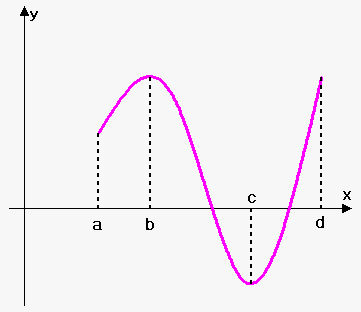
Consider function on the figure. It is increasing on interval ${\left[{a},{b}\right]}$ and ${\left[{c},{d}\right]}$, and decreasing on interval ${\left[{b},{c}\right]}$.

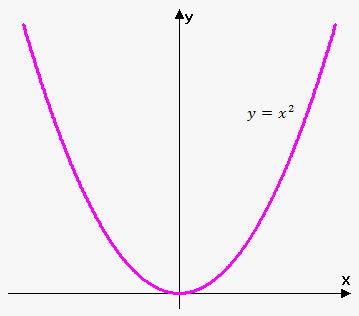
Function ${f{{\left({x}\right)}}}={{x}}^{{2}}$ is increasing on interval ${\left[{0},\infty\right)}$ and decreasing on interval ${\left(-\infty,{0}\right)}$.

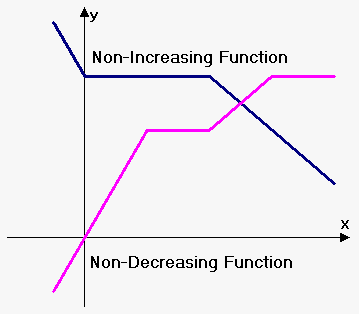The only difference between increasing and non-decreasing, decreasing and non-increasing is that function can take constant value on some subinterval(s) of $I$. See the figure to the right.