Even Odd Function

If ${f{{\left({x}\right)}}}={f{{\left(-{x}\right)}}}$ for every ${x}$ in the domain of ${f{}}$ then f is an even function.

For example, ${f{{\left({x}\right)}}}={{x}}^{{2}}$ is even because for every ${x}$ ${f{{\left(-{x}\right)}}}={{\left(-{x}\right)}}^{{2}}={{x}}^{{2}}={f{{\left({x}\right)}}}$ .

If ${f{{\left(-{x}\right)}}}=-{f{{\left({x}\right)}}}$ for every ${x}$ in the domain of ${f{}}$ then ${f{}}$ is an odd function.

For example, ${f{{\left({x}\right)}}}={{x}}^{{5}}$ is odd because for every ${x}$ ${f{{\left(-{x}\right)}}}={{\left(-{x}\right)}}^{{5}}=-{{x}}^{{5}}=-{f{{\left({x}\right)}}}$ .

Consider graph of the two functions: ${y}={{x}}^{{2}}$ and ${y}=\frac{{1}}{{4}}{{x}}^{{3}}$ .

even and odd functions

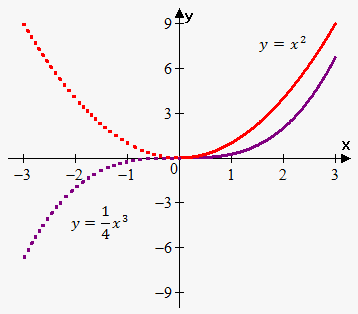
Since ${y}={{x}}^{{2}}$ is even function then we draw it on interval ${\left({0},\infty\right)}$ (red solid line) and then reflect it about y-axis (red dashed line)

Since ${y}=\frac{{1}}{{4}}{{x}}^{{3}}$ is odd function then we draw it on interval ${\left({0},\infty\right)}$ (purple solid line) and then reflect it about origin (purple dashed line). In other words we rotate graph ${{180}}^{{0}}$ counterclockwise.

Example 1. Determine whether function ${y}=\frac{{1}}{{{x}}^{{2}}}$ is even or odd.

Since ${f{{\left(-{x}\right)}}}=\frac{{1}}{{{{\left(-{x}\right)}}^{{2}}}}=\frac{{1}}{{{x}}^{{2}}}={f{{\left({x}\right)}}}$ then function is even.

Example 2. Determine whether function ${y}={{x}}^{{3}}-{x}$ is even or odd.

Since ${f{{\left(-{x}\right)}}}={{\left(-{x}\right)}}^{{3}}-{\left(-{x}\right)}={{x}}^{{3}}+{x}=-{\left({{x}}^{{3}}-{x}\right)}=-{f{{\left({x}\right)}}}$ then function is odd.

Example 3. Determine whether function ${y}={{x}}^{{3}}+{{x}}^{{2}}$ is even or odd.

Since ${f{{\left(-{x}\right)}}}={{\left(-{x}\right)}}^{{3}}+{{\left(-{x}\right)}}^{{2}}=-{{x}}^{{3}}+{{x}}^{{2}}$ then ${f{{\left(-{x}\right)}}}\ne{f{{\left({x}\right)}}}$ and ${f{{\left(-{x}\right)}}}\ne-{f{{\left({x}\right)}}}$ . This means that function is neither even, nor odd.