1. Home
  2. Math Notes
  3. Calculus I
  4. Function Types

Piecewise Function

When functions is determined by different formulas on different intervals then function is piecewise.

For example, f(x)={1−xifx<0x2ifx≥0{f{{\left({x}\right)}}}={\left\{\begin{array}{c}{1}-{x}{\quad\text{if}\quad}{x}<{0}\\{{x}}^{{2}}{\quad\text{if}\quad}{x}\ge{0}\\ \end{array}\right.} is piecewise because on interval (−∞,0){\left(-\infty,{0}\right)} f(x)=1−x{f{{\left({x}\right)}}}={1}-{x} and on interval [0,∞){\left[{0},\infty\right)} f(x)=x2{f{{\left({x}\right)}}}={{x}}^{{2}}. 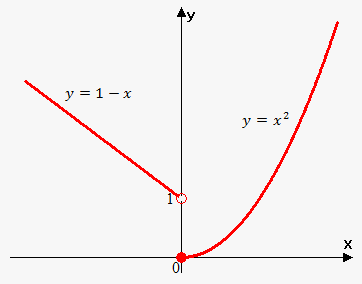piecewise function

Now find f(−2){f{{\left(-{2}\right)}}}, f(1){f{{\left({1}\right)}}}, f(0){f{{\left({0}\right)}}} and draw graph of this function.

Remember that function is a rule. In this case it tells us that if x<0{x}<{0} then apply f(x)=1−x{f{{\left({x}\right)}}}={1}-{x}, otherwise apply f(x)=x2{f{{\left({x}\right)}}}={{x}}^{{2}}.

Since −2<0-{2}<{0} then we apply f(x)=1−x{f{{\left({x}\right)}}}={1}-{x}: f(−2)=1−(−2)=3{f{{\left(-{2}\right)}}}={1}-{\left(-{2}\right)}={3}.

Since 1>0{1}>{0} then we apply f(x)=x2{f{{\left({x}\right)}}}={{x}}^{{2}}: f(1)=12=1{f{{\left({1}\right)}}}={{1}}^{{2}}={1}.

Since 0≥0{0}\ge{0} then we apply f(x)=x2{f{{\left({x}\right)}}}={{x}}^{{2}}: f(0)=02=0{f{{\left({0}\right)}}}={{0}}^{{2}}={0}.

Now, to draw this function we draw graph of the function f(x)=1−x{f{{\left({x}\right)}}}={1}-{x} on interval (−∞,0){\left(-\infty,{0}\right)} and graph of the function f(x)=x2{f{{\left({x}\right)}}}={{x}}^{{2}} on interval [0,∞){\left[{0},\infty\right)}.

Note, that open dot indicates that it doesn't belong to the graph. Indeed, f(0)=0{f{{\left({0}\right)}}}={0}, so point (0,0) is on the graph, but (0,1) is not.