Definition of Function
Suppose we are given two variables $$${x}$$$ and $$${y}$$$ with domain of variation $$${X}$$$ and $$${Y}$$$ respectively.
Suppose that $$${x}$$$ can take any value from $$${X}$$$ without any restrictions. Then variable $$${y}$$$ is called function of variable $$${x}$$$ in domain of its variation $$${X}$$$, if according to some law or rule we can assign to each value of $$${x}$$$ from $$${X}$$$ one definite value of $$${y}$$$ from $$${Y}$$$.
Independent variable $$${x}$$$ is also called argument of function.
Set $$${X}$$$ of values that can take independent variable $$${x}$$$ is called domain of function.
Note that sequence is particular case of function where domain is set of all natural numbers.
Set $$${Y}$$$ of values that can take dependent variable $$${y}$$$ is called range of function.
When we define a function we don't explictly state range of function, because it is automatically defined from domain of function and law of correspondence between $$${x}$$$ and $$${y}$$$.
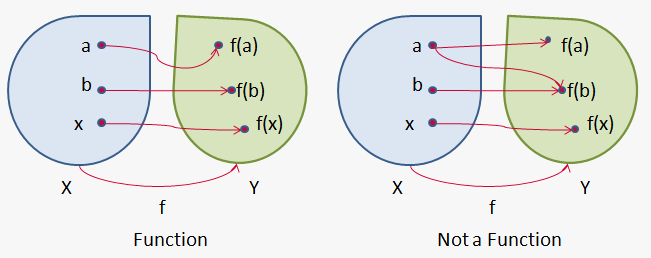
In definition we wrote that we assign to each value of $$${x}$$$ one value of $$${y}$$$. Actually we can to each value of $$${x}$$$ assign more than one value of $$${y}$$$. Such function is called multi-valued. In calculus we will consider only one-valued functions and even don't treat multi-valued function as function (see figure: to the right is not a function because when $$${x}={a}$$$ $$${y}$$$ takes two values).
To write that $$${y}$$$ is a function of $$${x}$$$ we write that $$${y}={f{{\left({x}\right)}}},{y}=\phi{\left({x}\right)},{y}={F}{\left({x}\right)}$$$ etc.
Letters $$${f},\phi,{F},..$$$ characterize rule that allows for every value of $$${x}$$$ find corresponding value of $$${y}.$$$ Therefore, if we consider different functions of same argument $$${x}$$$ then we should use different letters to denote them.
Of course we can use any letter to write functional dependence. Often we can even repeat letter $$${y}$$$: $$${y}={y}{\left({x}\right)}$$$.
If we consider function $$${y}={f{{\left({x}\right)}}}$$$ and want to write its particular value when $$${x}$$$ takes particular value $$${x}_{{0}}$$$, we write $$${f{{\left({x}_{{0}}\right)}}}$$$.
For example, if $$${f{{\left({x}\right)}}}=\frac{{1}}{{{1}+{{x}}^{{2}}}}$$$, $$${g{{\left({t}\right)}}}=\frac{{10}}{{t}}$$$, $$${h}{\left({u}\right)}=\sqrt{{{1}-{{u}}^{{2}}}}$$$ then
when $$${x}={1}$$$ $$${f{{\left({1}\right)}}}=\frac{{1}}{{{1}+{{1}}^{{2}}}}=\frac{{1}}{{2}}$$$; when $$${t}={5}$$$ $$${g{{\left({5}\right)}}}=\frac{{10}}{{5}}={2}$$$; when $$${u}={a}+{b}$$$ $$${h}{\left({a}+{b}\right)}=\sqrt{{{1}-{{\left({a}+{b}\right)}}^{{2}}}}$$$.
