We will obtain the trapezoidal rule (approximation) from averaging the right and left endpoint approximations : ∫ a b f ( x ) d x ≈ 1 2 ( L n + R n ) = 1 2 ( ∑ i = 1 n f ( x i − 1 ) Δ x + ∑ i = 1 n f ( x i ) Δ x ) {\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}\approx\frac{{1}}{{2}}{\left({L}_{{n}}+{R}_{{n}}\right)}=\frac{{1}}{{2}}{\left({\sum_{{{i}={1}}}^{{n}}}{f{{\left({x}_{{{i}-{1}}}\right)}}}\Delta{x}+{\sum_{{{i}={1}}}^{{n}}}{f{{\left({x}_{{i}}\right)}}}\Delta{x}\right)} ∫ a b f ( x ) d x ≈ 2 1 ( L n + R n ) = 2 1 ( ∑ i = 1 n f ( x i − 1 ) Δ x + ∑ i = 1 n f ( x i ) Δ x )
Rewriting it we obtain the trapezoidal rule : ∫ a b f ( x ) d x ≈ T n = Δ x 2 ( f ( x 0 ) + 2 f ( x 1 ) + 2 f ( x 2 ) + … + 2 f ( x n − 1 ) + f ( x n ) ) {\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}\approx{T}_{{n}}=\frac{{\Delta{x}}}{{2}}{\left({f{{\left({x}_{{0}}\right)}}}+{2}{f{{\left({x}_{{1}}\right)}}}+{2}{f{{\left({x}_{{2}}\right)}}}+\ldots+{2}{f{{\left({x}_{{{n}-{1}}}\right)}}}+{f{{\left({x}_{{n}}\right)}}}\right)}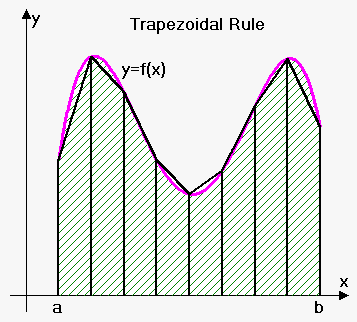 ∫ a b f ( x ) d x ≈ T n = 2 Δ x ( f ( x 0 ) + 2 f ( x 1 ) + 2 f ( x 2 ) + … + 2 f ( x n − 1 ) + f ( x n ) )
It is called trapezoidal because as appeared this formula gives approximation by approximating area not with rectangles but trapezoids, with height of trapezoid Δ x \Delta{x} Δ x f ( x i − 1 ) {f{{\left({x}_{{{i}-{1}}}\right)}}} f ( x i − 1 ) f ( x i ) {f{{\left({x}_{{i}}\right)}}} f ( x i ) Δ x ( f ( x i − 1 ) + f ( x i ) 2 ) \Delta{x}{\left(\frac{{{f{{\left({x}_{{{i}-{1}}}\right)}}}+{f{{\left({x}_{{i}}\right)}}}}}{{2}}\right)} Δ x ( 2 f ( x i − 1 ) + f ( x i ) )
It is worth noting that if function is concave up then trapezoidal rule overestimates integral, if function is concave down then trapezoidal rule underestimates integral.
Example 1 .∫ 1 2 1 x 2 d x {\int_{{1}}^{{2}}}\frac{{1}}{{{x}}^{{2}}}{d}{x} ∫ 1 2 x 2 1 d x n = 5 {n}={5} n = 5
Here a = 1 {a}={1} a = 1 b = 2 {b}={2} b = 2 f ( x ) = 1 x 2 {f{{\left({x}\right)}}}=\frac{{1}}{{{x}}^{{2}}} f ( x ) = x 2 1 n = 5 {n}={5} n = 5 Δ x = b − a n = 2 − 1 5 = 0.2 \Delta{x}=\frac{{{b}-{a}}}{{n}}=\frac{{{2}-{1}}}{{5}}={0.2} Δ x = n b − a = 5 2 − 1 = 0.2
So, ∫ 1 2 1 x 2 ( d x ) ≈ T n = 0.2 2 ( f ( 1 ) + 2 f ( 1.2 ) + 2 f ( 1.4 ) + 2 f ( 1.6 ) + 2 f ( 1.8 ) + f ( 2 ) ) = {\int_{{1}}^{{2}}}\frac{{1}}{{{x}}^{{2}}}{\left({d}{x}\right)}\approx{T}_{{n}}=\frac{{0.2}}{{2}}{\left({f{{\left({1}\right)}}}+{2}{f{{\left({1.2}\right)}}}+{2}{f{{\left({1.4}\right)}}}+{2}{f{{\left({1.6}\right)}}}+{2}{f{{\left({1.8}\right)}}}+{f{{\left({2}\right)}}}\right)}= ∫ 1 2 x 2 1 ( d x ) ≈ T n = 2 0.2 ( f ( 1 ) + 2 f ( 1.2 ) + 2 f ( 1.4 ) + 2 f ( 1.6 ) + 2 f ( 1.8 ) + f ( 2 ) ) =
= 0.1 ( 1 1 2 + 2 ( 1.2 ) 2 + 2 ( 1.4 ) 2 + 2 ( 1.6 ) 2 + 2 ( 1.8 ) 2 + 1 2 2 ) ≈ 0.505783 ={0.1}{\left(\frac{{1}}{{{1}}^{{2}}}+\frac{{2}}{{{\left({1.2}\right)}}^{{2}}}+\frac{{2}}{{{\left({1.4}\right)}}^{{2}}}+\frac{{2}}{{{\left({1.6}\right)}}^{{2}}}+\frac{{2}}{{{\left({1.8}\right)}}^{{2}}}+\frac{{1}}{{{2}}^{{2}}}\right)}\approx{0.505783} = 0.1 ( 1 2 1 + ( 1.2 ) 2 2 + ( 1.4 ) 2 2 + ( 1.6 ) 2 2 + ( 1.8 ) 2 2 + 2 2 1 ) ≈ 0.505783
In the Left Endpoint, Right Endpoint note we found for this example L n = 0.580783 {L}_{{n}}={0.580783} L n = 0.580783 R n = 0.430783 {R}_{{n}}={0.430783} R n = 0.430783
So, 1 2 ( L n + R n ) = 1 2 ( 0.580783 + 0.430783 ) = 0.505783 = T n \frac{{1}}{{2}}{\left({L}_{{n}}+{R}_{{n}}\right)}=\frac{{1}}{{2}}{\left({0.580783}+{0.430783}\right)}={0.505783}={T}_{{n}} 2 1 ( L n + R n ) = 2 1 ( 0.580783 + 0.430783 ) = 0.505783 = T n
True value of integral is I = ∫ 1 2 1 x 2 d x = 0.5 {I}={\int_{{1}}^{{2}}}\frac{{1}}{{{x}}^{{2}}}{d}{x}={0.5} I = ∫ 1 2 x 2 1 d x = 0.5
So, the trapezoidal rule overestimates integral as expected (function f ( x ) = 1 x 2 {f{{\left({x}\right)}}}=\frac{{1}}{{{x}}^{{2}}} f ( x ) = x 2 1 [ 1 , 2 ] {\left[{1},{2}\right]} [ 1 , 2 ]
When we approximate integral we will always have some error: E = ∫ a b f ( x ) d x − A p p {E}={\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}-{A}{p}{p} E = ∫ a b f ( x ) d x − A p p A p p {A}{p}{p} A p p E {E} E
Error bound for the trapezoidal rule. Suppose ∣ f ′ ′ ( x ) ∣ ≤ M {\left|{f{''}}{\left({x}\right)}\right|}\le{M} ∣ f ′′ ( x ) ∣ ≤ M a ≤ x ≤ b {a}\le{x}\le{b} a ≤ x ≤ b ∣ E ∣ ≤ M ( b − a ) 3 12 n 2 {\left|{E}\right|}\le\frac{{{M}{{\left({b}-{a}\right)}}^{{3}}}}{{{12}{{n}}^{{2}}}} ∣ E ∣ ≤ 12 n 2 M ( b − a ) 3
Example 2 .∫ 1 2 1 x 2 d x {\int_{{1}}^{{2}}}\frac{{1}}{{{x}}^{{2}}}{d}{x} ∫ 1 2 x 2 1 d x
Here a = 1 {a}={1} a = 1 b = 2 {b}={2} b = 2 f ( x ) = 1 x 2 {f{{\left({x}\right)}}}=\frac{{1}}{{{x}}^{{2}}} f ( x ) = x 2 1
Then f ′ ( x ) = − 2 x 3 {f{'}}{\left({x}\right)}=-\frac{{2}}{{{x}}^{{3}}} f ′ ( x ) = − x 3 2 f ′ ′ ( x ) = 6 x 4 {f{''}}{\left({x}\right)}=\frac{{6}}{{{x}}^{{4}}} f ′′ ( x ) = x 4 6
Therefore ∣ f ′ ′ ( x ) ∣ ≤ 6 {\left|{f{''}}{\left({x}\right)}\right|}\le{6} ∣ f ′′ ( x ) ∣ ≤ 6 1 ≤ x ≤ 2 {1}\le{x}\le{2} 1 ≤ x ≤ 2
Thus, 6 ( 2 − 1 ) 3 12 n 2 > 0.0002 \frac{{{6}{{\left({2}-{1}\right)}}^{{3}}}}{{{12}{{n}}^{{2}}}}>{0.0002} 12 n 2 6 ( 2 − 1 ) 3 > 0.0002 n 2 > 1 0.0004 {{n}}^{{2}}>\frac{{1}}{{{0.0004}}} n 2 > 0.0004 1
So, n > 1 0.0004 = 50 {n}>\frac{{1}}{\sqrt{{{0.0004}}}}={50} n > 0.0004 1 = 50
So, we need to take n = 51 {n}={51} n = 51
