Simpson's Rule

An idea of the Simpson's rule is in following: approximate curve by parabola and then find area of parabola (it is easy to do because we know antiderivative of quadratic function).

Again we divide ${\left[{a},{b}\right]}$ into ${n}$ subintervals of equal length $\Delta{x}=\frac{{{b}-{a}}}{{n}}$, and also require ${n}$ to be even number.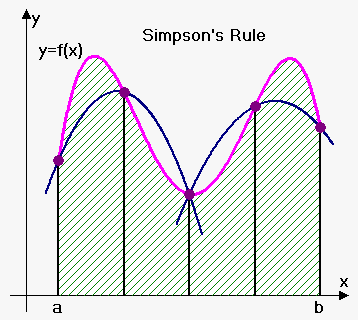

Then on each consecutive pair of intervals we approximate the curve ${y}={f{{\left({x}\right)}}}$ by a parabola. If ${y}_{{i}}={f{{\left({x}_{{i}}\right)}}}$, then ${P}_{{i}}={\left({x}_{{i}},{y}_{{i}}\right)}$ is the point on the curve lying above ${x}_{{i}}$.

A typical parabola passes through three consecutive points ${P}_{{i}}$, ${P}_{{{i}+{1}}}$ and ${P}_{{{i}+{2}}}$.

First we find equation of parabola that passes through points ${\left({x}_{{0}},{y}_{{0}}\right)}$, ${\left({x}_{{1}},{y}_{{1}}\right)}$ and ${\left({x}_{{2}},{y}_{{2}}\right)}$.

Also note that ${x}_{{1}}={x}_{{0}}+\Delta{x}$ and ${x}_{{2}}={x}_{{0}}+{2}\Delta{x}$.

Equation of any parabola has form ${y}={A}{{x}}^{{2}}+{B}{x}+{C}$ and so area under parabola from ${x}={x}_{{0}}$ to ${x}={x}_{{2}}={x}_{{0}}+{2}\Delta{x}$ is

${S}={\int_{{{x}_{{0}}}}^{{{x}_{{0}}+{2}\Delta{x}}}}{\left({A}{{x}}^{{2}}+{B}{x}+{C}\right)}{d}{x}={\left(\frac{{A}}{{3}}{{x}}^{{3}}+\frac{{B}}{{2}}{{x}}^{{2}}+{C}{x}\right)}{{\mid}_{{{x}_{{0}}}}^{{{x}_{{0}}+{2}\Delta{x}}}}=$

$={\left(\frac{{A}}{{3}}{{\left({x}_{{0}}+{2}\Delta{x}\right)}}^{{3}}+\frac{{B}}{{2}}{{\left({x}_{{0}}+{2}\Delta{x}\right)}}^{{2}}+{C}{\left({x}_{{0}}+{2}\Delta{x}\right)}\right)}-{\left(\frac{{A}}{{3}}{{x}_{{0}}^{{3}}}+\frac{{B}}{{2}}{{x}_{{0}}^{{2}}}+{C}{x}_{{0}}\right)}=$

$={2}{A}\Delta{x}{{x}_{{0}}^{{2}}}+{4}{A}{{\left(\Delta{x}\right)}}^{{2}}{x}_{{0}}+\frac{{8}}{{3}}{A}{{\left(\Delta{x}\right)}}^{{3}}+{2}{B}\Delta{x}{x}_{{0}}+{2}{B}{{\left(\Delta{x}\right)}}^{{2}}+{2}{C}\Delta{x}=$

$=\frac{{\Delta{x}}}{{3}}{\left({A}{\left({6}{{x}_{{0}}^{{2}}}+{12}\Delta{x}{x}_{{0}}+{8}{A}{{\left(\Delta{x}\right)}}^{{2}}\right)}+{B}{\left({6}{x}_{{0}}+{6}\Delta{x}\right)}+{6}{C}\right)}$.

Additionally parabola should pass through points ${P}_{{0}}={\left({x}_{{0}},{y}_{{0}}\right)}$, ${P}_{{1}}={\left({x}_{{1}},{y}_{{1}}\right)}$ and ${P}_{{2}}={\left({x}_{{2}},{y}_{{2}}\right)}$ (recall that ${x}_{{1}}={x}_{{0}}+\Delta{x}$ and ${x}_{{2}}={x}_{{0}}+{2}\Delta{x}$), so

${\left\{\begin{array}{c}{y}_{{0}}={A}{{x}_{{0}}^{{2}}}+{B}{x}_{{0}}+{C}\\{y}_{{1}}={A}{{\left({x}_{{0}}+\Delta{x}\right)}}^{{2}}+{B}{\left({x}_{{0}}+\Delta{x}\right)}+{C}\\{y}_{{2}}={A}{{\left({x}_{{0}}+{2}\Delta{x}\right)}}^{{2}}+{B}{\left({x}_{{0}}+{2}\Delta{x}\right)}+{C}\\ \end{array}\right.}$

From this we have that

${y}_{{0}}+{4}{y}_{{1}}+{y}_{{2}}=$

$={A}{{x}_{{0}}^{{2}}}+{B}{x}_{{0}}+{C}+{4}{\left({A}{{\left({x}_{{0}}+\Delta{x}\right)}}^{{2}}+{B}{\left({x}_{{0}}+\Delta{x}\right)}+{C}\right)}+{A}{{\left({x}_{{0}}+{2}\Delta{x}\right)}}^{{2}}+{B}{\left({x}_{{0}}+{2}\Delta{x}\right)}+{C}=$

$={A}{\left({6}{{x}_{{0}}^{{2}}}+{12}\Delta{x}{x}_{{0}}+{8}{{\left(\Delta{x}\right)}}^{{2}}\right)}+{B}{\left({6}{x}_{{0}}+{6}\Delta{x}\right)}+{6}{C}$.

If we know multiply both sides of equality by $\frac{{\Delta{x}}}{{3}}$ we will obtain that

$\frac{{\Delta{x}}}{{3}}{\left({y}_{{0}}+{4}{y}_{{1}}+{y}_{{2}}\right)}=\frac{{\Delta{x}}}{{3}}{\left({A}{\left({6}{{x}_{{0}}^{{2}}}+{12}\Delta{x}{x}_{{0}}+{8}{{\left(\Delta{x}\right)}}^{{2}}\right)}+{B}{\left({6}{x}_{{0}}+{6}\Delta{x}\right)}+{6}{C}\right)}$.

But right side is exactly area ${S}$ under parabola.

Therefore, ${S}=\frac{{\Delta{x}}}{{3}}{\left({y}_{{0}}+{4}{y}_{{1}}+{y}_{{2}}\right)}$.

Similarly, it can be shown that the area under parabola through ${P}_{{2}}$, ${P}_{{3}}$ and ${P}_{{4}}$ from ${x}={x}_{{2}}$ to ${x}={x}_{{4}}$ is $\frac{{\Delta{x}}}{{3}}{\left({y}_{{2}}+{4}{y}_{{3}}+{y}_{{4}}\right)}$.

In general, area under parabola through ${P}_{{i}}$, ${P}_{{{i}+{1}}}$, ${P}_{{{i}+{2}}}$ from ${x}={x}_{{i}}$ to ${x}={x}_{{{i}+{2}}}$ is $\frac{{\Delta{x}}}{{3}}{\left({y}_{{i}}+{y}_{{{i}+{1}}}+{y}_{{{i}+{2}}}\right)}$.

Summing areas under parabolas on each subinterval we will obtain that ${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}\approx\frac{{\Delta{x}}}{{3}}{\left({y}_{{0}}+{4}{y}_{{1}}+{y}_{{2}}\right)}+\frac{{\Delta{x}}}{{3}}{\left({y}_{{2}}+{4}{y}_{{3}}+{y}_{{4}}\right)}+\ldots+\frac{{\Delta{x}}}{{3}}{\left({y}_{{{n}-{2}}}+{4}{y}_{{{n}-{1}}}+{y}_{{n}}\right)}$.

where ${n}$ is even and $\Delta{x}=\frac{{{b}-{a}}}{{n}}$.

Note the pattern of coeffcients: 1,4,2,4,2,4,2,4,2,...,4,2,4,2,4,2,4,1.

When we approximate integral we will always have some error: ${E}={\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}-{A}{p}{p}$ where ${A}{p}{p}$ is approximation and ${E}$ is error.

Error Bound for Simpson's Rule. Suppose ${\left|{{f}}^{{{\left({4}\right)}}}{\left({x}\right)}\right|}\le{M}$ for ${a}\le{x}\le{b}$ then ${\left|{E}\right|}\le\frac{{{M}{{\left({b}-{a}\right)}}^{{5}}}}{{{180}{{n}}^{{4}}}}$.