Concept of Antiderivative and Indefinite Integral

In the Calculus I (Differential Calculus) section, our main purpose was to find the derivative of a given function.

But often we need to solve the inverse task: given a function ${f{{\left({x}\right)}}}$ , we need to find the function ${F}{\left({x}\right)}$ whose derivative is ${f{{\left({x}\right)}}}$ . In other words, we need to find a function ${F}{\left({x}\right)}$ such that ${F}'{\left({x}\right)}={f{{\left({x}\right)}}}$ .

Indeed, suppose that we are given the velocity of an object ${v}{\left({t}\right)}$ and need to find its position function ${s}{\left({t}\right)}.$ Since ${s}'{\left({t}\right)}={v}{\left({t}\right)}$ , this leads us to the inverse task. Similarly, we may want to find the velocity ${v}{\left({t}\right)}$ of an object knowing its acceleration ${a}{\left({t}\right)}$ . Since ${v}'{\left({t}\right)}={a}{\left({t}\right)}$ , we again need to solve the inverse task.

Definition. A function ${F}$ is called the antiderivative of ${f{}}$ on an interval ${I}$ if ${F}'{\left({x}\right)}={f{{\left({x}\right)}}}$ for all ${x}$ in ${I}$ .

Example 1. Find the antiderivative of ${f{{\left({x}\right)}}}={{x}}^{{2}}$ .

It is not difficult to discover the antiderivative of ${{x}}^{{2}}$ if you know the derivative of the power function.

In fact, if ${F}{\left({x}\right)}=\frac{{1}}{{3}}{{x}}^{{3}}$ , then ${F}'{\left({x}\right)}={{x}}^{{2}}={f{{\left({x}\right)}}}$ .

But the function ${G}{\left({x}\right)}=\frac{{1}}{{3}}{{x}}^{{3}}+{1}$ also satisfies ${G}'{\left({x}\right)}={{x}}^{{2}}={f{{\left({x}\right)}}}$ .

Therefore, both ${F}$ and ${G}$ are antiderivatives of ${f{}}$ .

In general, any function of the form $\frac{{1}}{{3}}{{x}}^{{3}}+{C}$ , where ${C}$ is a constant, is an antiderivative of ${{x}}^{{2}}$ .

The following fact says that ${f{}}$ has no other antiderivatives.

Fact. If ${F}{\left({x}\right)}$ is an antiderivative of ${f{{\left({x}\right)}}}$ on ${I}$ , then the most general antiderivative of ${f{}}$ on ${I}$ is ${F}{\left({x}\right)}+{C}$ , where ${C}$ is an arbitrary constant.

Example 2. Find the general antiderivative of ${{x}}^{{n}}$ , ${n}\ne-{1}$ .

Since ${\left(\frac{{{{x}}^{{{n}+{1}}}}}{{{n}+{1}}}\right)}'={{x}}^{{n}}$ , the general antiderivative of ${{x}}^{{n}}$ is $\frac{{{{x}}^{{{n}+{1}}}}}{{{n}+{1}}}+{C}$ , ${n}\ne-{1}$ .

In fact, the antiderivative arises so often that it is given a special name and notation.

Definition. The expression ${F}{\left({x}\right)}+{C}$ , where ${C}$ is an arbitrary constant, that is the most general antiderivative of the function ${f{{\left({x}\right)}}}$ , is called the indefinite integral of ${f{{\left({x}\right)}}}$ and is denoted by $\int{f{{\left({x}\right)}}}{d}{x}$ .

In other words, $\int{f{{\left({x}\right)}}}{d}{x}={F}{\left({x}\right)}+{C}$ , where ${C}$ is an arbitrary constant.

The sign $\int$ was introduced by Leibniz and is called the integral sign. ${f{{\left({x}\right)}}}$ is called the integrand.

The process of finding the indefinite integral (or general antiderivative) is called integration.
Also, bear in mind that some functions can't be integrated; in other words, the integral of some functions can't be done in terms of the functions we know. Examples of such functions are $\int\frac{{{{e}}^{{x}}}}{{x}}{d}{x}$ , $\int{\cos{{\left({{x}}^{{2}}\right)}}}{d}{x}$ , etc.

Now, returning to the position, velocity, and acceleration functions, we can write that

${s}{\left({t}\right)}=\int{v}{\left({t}\right)}{d}{t}$ ;
${v}{\left({t}\right)}=\int{a}{\left({t}\right)}{d}{t}$ .

Example 3. Find $\int{\cos{{\left({x}\right)}}}{d}{x}$ .

Since ${\left({\sin{{\left({x}\right)}}}\right)}'={\cos{{\left({x}\right)}}}$ , the antiderivative of ${\cos{{\left({x}\right)}}}$ is ${\sin{{\left({x}\right)}}}$ , so the general antiderivative (indefinite integral) is $\int{\cos{{\left({x}\right)}}}{d}{x}={\sin{{\left({x}\right)}}}+{C}$ , where ${C}$ is an arbitrary constant.

Since the indefinite integral (general antiderivative) is given by a family of functions, it is impossible to define some particular function without defining certain additional conditions. To define a particular function, we can add a condition of the form ${F}{\left({a}\right)}={b}$ .

Example 4. Find $\int{{x}}^{{4}}{d}{x}$ if ${F}{\left({1}\right)}={2}$ .

Since ${\left(\frac{{1}}{{5}}{{x}}^{{5}}\right)}'={{x}}^{{4}}$ , we have that $\int{{x}}^{{4}}{d}{x}=\frac{{1}}{{5}}{{x}}^{{5}}+{C}$ .

That is, ${F}{\left({x}\right)}=\frac{{1}}{{5}}{{x}}^{{5}}+{C}$ . To define the particular function (i.e. the constant ${C}$ ), we use the condition ${F}{\left({1}\right)}={2}$ :

${2}={F}{\left({1}\right)}=\frac{{1}}{{5}}\cdot{{1}}^{{5}}+{C}$ . From this, ${C}=\frac{{9}}{{5}}$ .

So, ${F}{\left({x}\right)}=\frac{{1}}{{5}}{{x}}^{{5}}+\frac{{9}}{{5}}$ .

Now, let's study the geometric meaning of the indefinite integral.

Since the derivative is the slope of the tangent line at a point ${a}$ , the indefinite integral is a function ${F}{\left({x}\right)}$ the tangent line to which at the point ${a}$ equals ${f{{\left({a}\right)}}}$ .

Example 5. We are given that ${f{{\left({x}\right)}}}=\sqrt{{{1}+{{x}}^{{2}}}}$ . Use it to sketch the graph of the indefinite integral ${F}{\left({x}\right)}.$

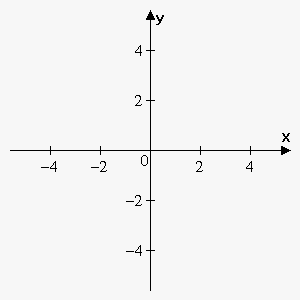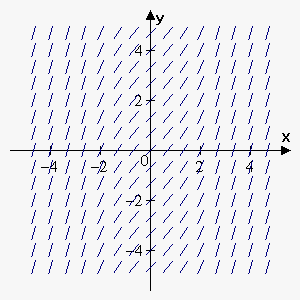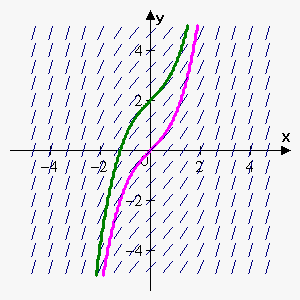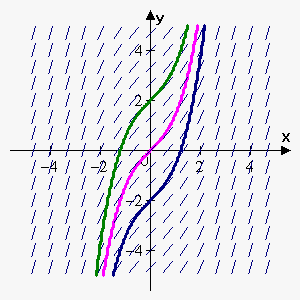Recall that the slope of the tangent line to the indefinite integral at a point ${a}$ is ${f{{\left({a}\right)}}}$ .

So, we calculate that ${f{{\left({0}\right)}}}=\sqrt{{{1}+{{0}}^{{2}}}}={1}$ , ${f{{\left({2}\right)}}}=\sqrt{{{1}+{{2}}^{{2}}}}=\sqrt{{{5}}}\approx{2.24}$ , etc.

This means that the slope of the tangent line at the point $0$ will be $1$ , the slope of the tangent line at the point $2$ will be approximately $2.24$ . Now, we draw several tangent segments with the slope $1$ at the point $x=0$ and several tangent segments with the slope $2.24$ at ${x}={2}$ . Continuing this process, we obtain the slopes of the tangents at all the points. This is called a direction field because it shows the direction of ${F}{\left({x}\right)}$ at all the points.

Now, we can draw several curves that follow the direction of the tangent segments. If we want a particular curve, then we need an additional condition. For example, only the green curve satisfies the condition ${F}{\left({0}\right)}={2}$ .

Note that all curves can be obtained from each other by shifting upward or downward.