Power Function

Depending on value of ${n}$ graph of power function has different forms and properties.

Case 1: ${n}$ is positive integer.

When ${n}={1}$ we obtain line ${y}={x}$. When ${n}={2}$ we obtain parabola ${y}={{x}}^{{2}}$. When ${n}={3}$ we obtain cubic function ${y}={{x}}^{{3}}$.

Graph of function depends on whether ${n}$ is even or odd.

If ${n}$ is even then functions of the form ${f{{\left({x}\right)}}}={{x}}^{{n}}$ are even and their graphs are similar to the graph of function ${y}={{x}}^{{2}}$.

If ${n}$ is odd then functions of the form ${f{{\left({x}\right)}}}={{x}}^{{n}}$ are odd and their graphs are similar to the graph of function ${y}={{x}}^{{3}}$.

Note, that when ${\left|{x}\right|}<{1}$ the bigger ${n}$, the closer graph to x-axis. For ${\left|{x}\right|}>{1}$ the bigger ${n}$, the faster functions grows (the further from x-axis).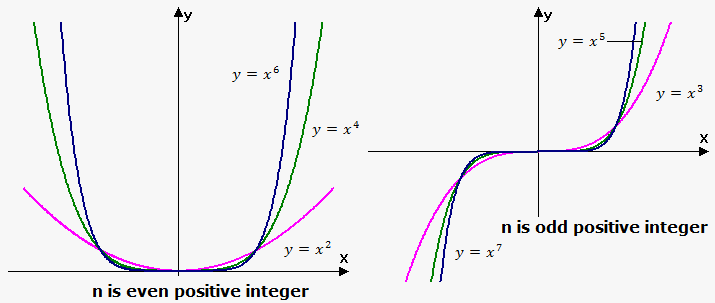

Case 2: ${n}$ is negative integer, i.e. ${n}=-{a}$ where ${a}$ is positive integer.

Domain of such functions is all ${x}$ except ${x}={0}$ (function is nor defined when denominator equals 0).

When ${n}={1}$ we obtain hyperbola ${y}=\frac{{1}}{{x}}$.

Graph of function depends on whether ${n}$ is even or odd.

If ${n}$ is even then functions are even and their graphs are similar to the graph of function ${y}=\frac{{1}}{{{x}}^{{2}}}$.

If ${n}$ is odd then functions are odd and their graphs are similar to the graph of function ${y}=\frac{{1}}{{x}}$.

Note, that when ${\left|{x}\right|}<{1}$ the bigger ${n}$, the furthe graph to x-axis. For ${\left|{x}\right|}>{1}$ the bigger ${n}$, the closer function to the x-axis.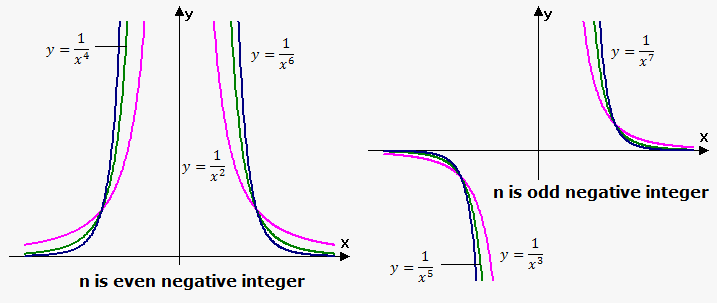

Case 3: ${n}$ is irreducible fraction, i.e. ${n}=\frac{{a}}{{b}}$ where ${a}$ and ${b}$ are integers.

Domain of such functions depends on ${a}$ and ${b}$. Remember that we can't extract even-degree root of negative number.

First consider case when $\frac{{a}}{{b}}$ is positive.

In this case ${{x}}^{{\frac{{a}}{{b}}}}={\sqrt[{{b}}]{{{{x}}^{{a}}}}}$. If b is odd then domain is interval ${\left(-\infty,\infty\right)}$. If b is even then a is odd (remember that $\frac{{a}}{{b}}$ is irreducible, so ${a}$ and ${b}$ can't be both even) then domain is interval ${\left[{0},+\infty\right)}$.

Now consider case when $\frac{{a}}{{b}}$ is negative, i.e. $\frac{{a}}{{b}}=-\frac{{m}}{{k}}$ where ${m}$ and ${k}$ are positive integers.

In this case ${{x}}^{{\frac{{a}}{{b}}}}=\frac{{1}}{{{\sqrt[{{k}}]{{{{x}}^{{m}}}}}}}$. If k is odd then domain is interval ${\left(-\infty,\infty\right)}$, except ${x}={0}$. If k is even then m is odd (remember that $\frac{{m}}{{k}}$ is irreducible, so m and k can't be both even) then domain is interval ${\left({0},+\infty\right)}$.

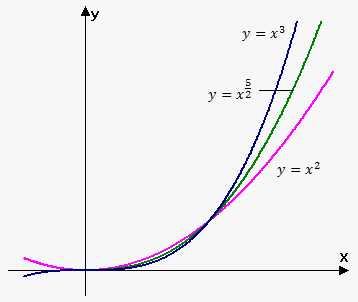
For example, domain of ${y}={{x}}^{{\frac{{5}}{{2}}}}$ is ${\left({0}+\infty\right)}$. Domain of the ${y}={{x}}^{{-\frac{{5}}{{2}}}}$ is ${\left({0}+\infty\right)}$.

For case when ${n}$ is rational graph will lie between graphs of power functions with closest integer values.

For example, graph of the function ${y}={{x}}^{{\frac{{5}}{{2}}}}$ will lie between graphs of functions ${y}={{x}}^{{2}}$ and ${y}={{x}}^{{3}}$ because ${2}<\frac{{5}}{{2}}<{3}$. See figure to the left.