Polynomial Function
Polynomial is a function of the form $$${y}={f{{\left({x}\right)}}}={a}_{{n}}{{x}}^{{n}}+{a}_{{{n}-{1}}}{{x}}^{{{n}-{1}}}+\ldots+{a}_{{2}}{{x}}^{{2}}+{a}_{{1}}{x}+{a}_{{0}}$$$, where n is nonnegative integer and $$${a}_{{0}},\ {a}_{{1}},\ \ldots,\ {a}_{{{n}-{1}}},\ {a}_{{n}}$$$ are constants which are called coefficients of polynomial.
Domain of any polynomial is $$${\left(-\infty,\infty\right)}$$$.
If $$${a}_{{n}}\ne{0}$$$ then $$${n}$$$ is the degree of polynomial. For example, $$${f{{\left({x}\right)}}}=-{2}{{x}}^{{5}}+{3}{x}+\sqrt{{{3}}}$$$ is a polynomial of degree 5.
If degree of polynomial is n=1, then $$${\color{blue}{{{f{{\left({x}\right)}}}={m}{x}+{b}}}}$$$ and it is linear function.
In case degree is 2 then $$${\color{red}{{{f{{\left({x}\right)}}}={a}{{x}}^{{2}}+{b}{x}+{c}}}}$$$ and this function is called quadratic.
A polynomial of degree 3 $$${\color{green}{{{f{{\left({x}\right)}}}={a}{{x}}^{{3}}+{b}{{x}}^{{2}}+{c}{x}+{d}}}}$$$ is called cubic function.
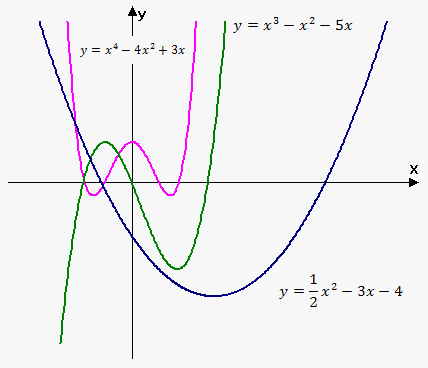
Graph of polynomial functions have different shapes. On the figure you can see graph of polynomials with degree $$${n}={2},{3},{4}$$$.