Linear Function
Linear function is given as $$${y}={f{{\left({x}\right)}}}={m}{x}+{b}$$$.
$$${m}$$$ is called slope and $$${b}$$$ is called y-intercept. Graph of the linear function is line. Since there are two parameters in the linear function (m and b) it is enough two points to uniquely identify line.
If line passes through 2 points $$${\left({x}_{{1}},{y}_{{1}}\right)}$$$ and $$${\left({x}_{{2}},{y}_{{2}}\right)}$$$ then $$${\color{blue}{{{m}=\frac{{{y}_{{2}}-{y}_{{1}}}}{{{x}_{{2}}-{x}_{{1}}}}}}}$$$.
$$${m}$$$ shows rate of change of function. For example, for function $$${y}={3}{x}+{2}$$$ if we increase $$${x}$$$ by 1 unit, then $$${y}$$$ will increase by 3 units. A characteristic feature of linear functions is that they grow at a constant rate.
Sometimes linear function can be given in the form $$${a}{x}+{c}{y}={d}$$$, where $$${c}\ne{0}$$$. We can easily convert it into standard form by dividing both sides of equation by $$${c}$$$: $$${y}=-\frac{{a}}{{c}}{x}+\frac{{d}}{{c}}$$$. Here $$${m}=-\frac{{a}}{{c}}$$$ and $$${b}=\frac{{d}}{{c}}$$$.
Example 1. Find equation of line that passes through points $$${\left({2},-{3}\right)}$$$ and $$${\left(-{5},{1}\right)}$$$.
Slope of the line is $$${m}=\frac{{{1}-{\left(-{3}\right)}}}{{-{5}-{2}}}=-\frac{{4}}{{7}}$$$.
Now, equation of line can be rewritten as $$${y}=-\frac{{4}}{{7}}{x}+{b}$$$. Since line passes through point $$${\left({2},-{3}\right)}$$$ then $$$-{3}=-\frac{{4}}{{7}}\cdot{2}+{b}$$$. From this $$${b}=-\frac{{13}}{{7}}$$$.
Thus, equation of line is $$${y}=-\frac{{4}}{{7}}{x}-\frac{{13}}{{7}}$$$.
Example 2. Draw line whose equation is $$${3}{x}+{2}{y}={6}$$$.
We need to points to draw a graph.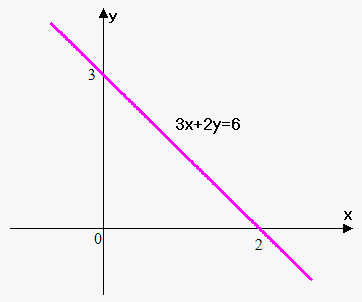
If $$${x}={0}$$$ then $$${3}\cdot{0}+{2}{y}={6}$$$ or $$${y}={3}$$$. Therefore, first point is $$${\left({0},{3}\right)}$$$.
If $$${y}={0}$$$ then $$${3}{x}+{2}\cdot{0}={6}$$$ or $$${x}={2}$$$. Therefore, second point is $$${\left({2},{0}\right)}$$$.
Now draw two found points and line through them.
Graph is shown on figure.
Suppose that we have two lines $$${y}={m}_{{1}}{x}+{b}_{{1}}$$$ and $$${y}={m}_{{2}}{x}+{b}_{{2}}$$$.
Lines are parallel if $$${m}_{{1}}={m}_{{2}}$$$. If in addition $$${b}_{{1}}={b}_{{2}}$$$ then lines are same.
Lines are perpendicular if $$${m}_{{1}}{m}_{{2}}=-{1}$$$.
Example 3. Find equation of line that is perpendicular to line $$${4}{x}+{3}{y}={2}$$$ and passes through point $$${\left(-{1},{3}\right)}$$$.
Let's rewrite given line in standard form: $$${y}=-\frac{{4}}{{3}}{x}+\frac{{2}}{{3}}$$$.
If slope of required line is $$${m}$$$, then since lines are perpendicular we have that $$${m}\cdot{\left(-\frac{{4}}{{3}}\right)}=-{1}$$$ or $$${m}=\frac{{3}}{{4}}$$$.
Thus, equation of line is $$${y}=\frac{{3}}{{4}}{x}+{b}$$$. To find constant $$${b}$$$ we use the fact that line passes through point $$${\left(-{1},{3}\right)}$$$: $$${3}=\frac{{3}}{{4}}\cdot{\left(-{1}\right)}+{b}$$$ or $$${b}=\frac{{15}}{{4}}$$$.
So, equation of line is $$${y}=\frac{{3}}{{4}}{x}+\frac{{15}}{{4}}$$$ or $$${4}{y}-{3}{x}={15}$$$.
