Definition of Convex and Concave Functions
 Consider two functions on the figure to the right.
Consider two functions on the figure to the right.
They are both increasing, but their form is different.
That's because one of them is convex and another is concave.
Definition. Function $$$y={f{{\left({x}\right)}}}$$$ that is defined and continuous on interval $$$X$$$ is called convex (or convex downward or concave upward) if for any $$$a$$$ and $$$b$$$ from $$$X$$$ and numbers $$${q}_{{1}}$$$ and $$${q}_{{2}}$$$ such that $$${q}_{{1}}+{q}_{{2}}={1}$$$ and $$${q}_{{1}}\ge{0},{q}_{{2}}\ge{0}$$$ we have that $$${f{{\left({q}_{{1}}{a}+{q}_{{2}}{b}\right)}}}\le{q}_{{1}}{f{{\left({a}\right)}}}+{q}_{{2}}{f{{\left({b}\right)}}}$$$.
Similarly we have the following definition of concave function.
Definition. Function $$${y}={f{{\left({x}\right)}}}$$$ that is defined and continuous on interval $$${X}$$$ is called concave (or convex upward or concave downward) if for any $$${a}$$$ and $$${b}$$$ from $$${X}$$$ and numbers $$${q}_{{1}}$$$ and $$${q}_{{2}}$$$ such that $$${q}_{{1}}+{q}_{{2}}={1}$$$ and $$${q}_{{1}}\ge{0},{q}_{{2}}\ge{0}$$$ we have that $$${f{{\left({q}_{{1}}{a}+{q}_{{2}}{b}\right)}}}\ge{q}_{{1}}{f{{\left({a}\right)}}}+{q}_{{2}}{f{{\left({b}\right)}}}$$$.
From definition it follows that if $$${f{{\left({x}\right)}}}$$$ is concave upward then $$$-{f{{\left({x}\right)}}}$$$ is concave downward, and vice versa. This fact allows us to study mainly only concave upward functions.
Definition. Function $$${y}={f{{\left({x}\right)}}}$$$ that is defined and continuous on interval $$${X}$$$ is called strictly convex if for any $$$a$$$ and $$$b$$$ $$$\left({a}\ne{b}\right)$$$ from $$$X$$$ and numbers $$${q}_{{1}}$$$ and $$${q}_{{2}}$$$ such that $$${q}_{{1}}+{q}_{{2}}={1}$$$ and $$${q}_{{1}}>{0},{q}_{{2}}>{0}$$$ we have that $$${f{{\left({q}_{{1}}{a}+{q}_{{2}}{b}\right)}}}<{q}_{{1}}{f{{\left({a}\right)}}}+{q}_{{2}}{f{{\left({b}\right)}}}$$$.
Similarly we have the following definition of strictly concave function.
Definition. Function $$${y}={f{{\left({x}\right)}}}$$$ that is defined and continuous on interval $$${X}$$$ is called strictly concave if for any $$${a}$$$ and $$${b}$$$ $$$\left({a}\ne{b}\right)$$$ from $$${X}$$$ and numbers $$${q}_{{1}}$$$ and $$${q}_{{2}}$$$ such that $$${q}_{{1}}+{q}_{{2}}={1}$$$ and $$${q}_{{1}}>{0},{q}_{{2}}>{0}$$$ we have that $$${f{{\left({q}_{{1}}{a}+{q}_{{2}}{b}\right)}}}>{q}_{{1}}{f{{\left({a}\right)}}}+{q}_{{2}}{f{{\left({b}\right)}}}$$$.
Clearly if function is strictly concave upward (downward) then it is concave upward (downward).
Now, let's see what is the geometric meaning of the concave functions.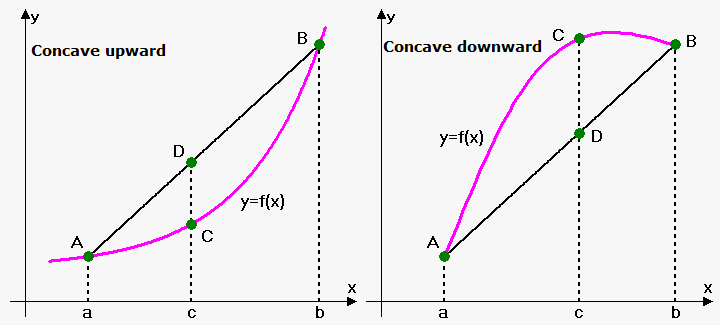
Without loss of generality assume that $$${a}<{b}$$$. Since $$${q}_{{1}}+{q}_{{2}}={1}$$$, and $$${q}_{{1}}$$$ and $$${q}_{{2}}$$$ are non-negative then expression $$${c}={q}_{{1}}{a}+{q}_{{2}}{b}$$$ is between $$${a}$$$ and $$${b}$$$, in other words $$${a}\le{q}_{{1}}{a}+{q}_{{2}}{b}\le{b}$$$.
Now, consider points $$${A}{\left({a},{f{{\left({a}\right)}}}\right)}$$$ and $$${B}{\left({b},{f{{\left({b}\right)}}}\right)}$$$. Draw line through them. Point $$${C}={\left({c},{f{{\left({c}\right)}}}\right)}$$$ lies on the graph of function between points $$${a}$$$ and $$${b}$$$. y-coordinate of point with x-coordinate $$${c}$$$ that lies on the line is $$${q}_{{1}}{f{{\left({a}\right)}}}+{q}_{{2}}{f{{\left({b}\right)}}}$$$. So, let we have another point $$${D}{\left({c},{q}_{{1}}{f{{\left({a}\right)}}}+{q}_{{2}}{f{{\left({b}\right)}}}\right)}$$$.
Thus, function is concave upward if all values of function on interval $$${\left[{a},{b}\right]}$$$ lie below line that connects $$${\left({a},{f{{\left({a}\right)}}}\right)}$$$ and $$${\left({b},{f{{\left({b}\right)}}}\right)}$$$.
Function is concave downward if all values of function on interval $$${\left[{a},{b}\right]}$$$ lie above line that connects $$${\left({a},{f{{\left({a}\right)}}}\right)}$$$ and $$${\left({b},{f{{\left({b}\right)}}}\right)}$$$.
Example 1. The most trivial example of both concave upward and concave downward function is linear function $$${f{{\left({x}\right)}}}={m}{x}+{b}$$$. For it inequality in definition transforms into equality.
Example 2. Function $$${y}={{x}}^{{2}}$$$ is strictly concave upward. We can check it using definition.
$$${f{{\left({q}_{{1}}{a}+{q}_{{2}}{b}\right)}}}={{\left({q}_{{1}}{a}+{q}_{{2}}{b}\right)}}^{{2}}={{q}_{{1}}^{{2}}}{{a}}^{{2}}+{{q}_{{2}}^{{2}}}{{b}}^{{2}}+{2}{q}_{{1}}{q}_{{2}}{a}{b}={q}_{{1}}{q}_{{1}}{{a}}^{{2}}+{q}_{{2}}{q}_{{2}}{{b}}^{{2}}+{2}{q}_{{1}}{q}_{{2}}{a}{b}$$$.
We know that $$${q}_{{1}}+{q}_{{2}}={1}$$$ so we replace $$${q}_{{2}}$$$ with $$${1}-{q}_{{1}}$$$ and $$${q}_{{1}}$$$ with $$${1}-{q}_{{2}}$$$:
$$${q}_{{1}}{\left({1}-{q}_{{2}}\right)}{{a}}^{{2}}+{q}_{{2}}{\left({1}-{q}_{{1}}\right)}{{b}}^{{2}}+{2}{q}_{{1}}{q}_{{2}}{a}{b}={q}_{{1}}{{a}}^{{2}}-{q}_{{1}}{q}_{{2}}{{a}}^{{2}}+{q}_{{2}}{{b}}^{{2}}-{q}_{{1}}{q}_{{2}}{{b}}^{{2}}+{2}{q}_{{1}}{q}_{{2}}{a}{b}=$$$
$$$={q}_{{1}}{{a}}^{{2}}+{q}_{{2}}{{b}}^{{2}}-{q}_{{1}}{q}_{{2}}{{\left({a}-{b}\right)}}^{{2}}$$$.
Since $$${q}_{{1}}>{0}$$$, $$${q}_{{2}}>{0}$$$ and $$${{\left({a}-{b}\right)}}^{{2}}>{0}$$$ then $$${q}_{{1}}{q}_{{2}}{{\left({a}-{b}\right)}}^{{2}}>{0}$$$ and $$$-{q}_{{1}}{q}_{{2}}{{\left({a}-{b}\right)}}^{{2}}<{0}$$$, so
$$${q}_{{1}}{{a}}^{{2}}+{q}_{{2}}{{b}}^{{2}}-{q}_{{1}}{q}_{{2}}{{\left({a}-{b}\right)}}^{{2}}<{q}_{{1}}{{a}}^{{2}}+{q}_{{2}}{{b}}^{{2}}={q}_{{1}}{f{{\left({a}\right)}}}+{q}_{{2}}{f{{\left({b}\right)}}}$$$.
Therefore, $$${f{{\left({q}_{{1}}{a}+{q}_{{2}}{b}\right)}}}<{q}_{{1}}{f{{\left({a}\right)}}}+{q}_{{2}}{f{{\left({b}\right)}}}$$$. This proves that function $$${y}={{x}}^{{2}}$$$ is strictly concave upward. And also it is simply concave upward.
