Properties of Definite Integrals

Now let's see what properties integral has.

Property 1. It follows from the definition of integral that $$${\int_{{a}}^{{a}}}{f{{\left({x}\right)}}}{d}{x}={0}$$$.

Property 2. Inverting bounds of integration: $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}=-{\int_{{b}}^{{a}}}{f{{\left({x}\right)}}}{d}{x}$$$.

Property 3. If $$${f{}}$$$ is an even function then $$${\int_{{-{a}}}^{{a}}}{f{{\left({x}\right)}}}{d}{x}={2}{\int_{{0}}^{{a}}}{f{{\left({x}\right)}}}{d}{x}$$$.

In terms of areas, this means the following: if $$${f{}}$$$ is symmetric about the x-axis, then the area from $$$-{a}$$$ to 0 equals the area from $$${0}$$$ to $$${a}$$$.

Property 4. If $$${f{}}$$$ is an odd function then $$${\int_{{-{a}}}^{{a}}}{f{{\left({x}\right)}}}{d}{x}={0}$$$.

In terms of areas, this means the following: if $$${f{}}$$$ is symmteric about the origin, then the area from $$$-{a}$$$ to 0 equals minus area from $$${0}$$$ to $$${a}$$$. This means that net area is 0.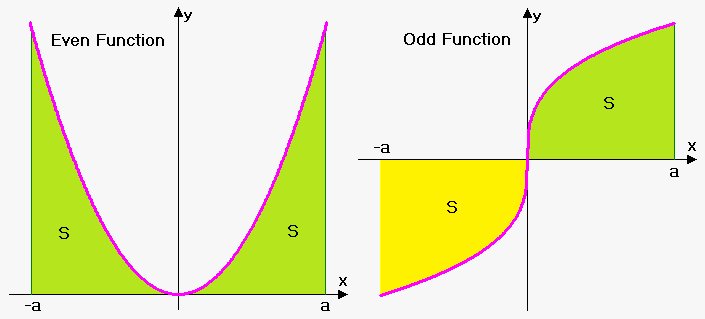 symmetry of integral

Integral Adjacency: $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}={\int_{{a}}^{{c}}}+{\int_{{c}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}$$$ for any displacement of points $$${a}$$$, $$${b}$$$ and $$${c}$$$.

Example 1. It is known that $$${\int_{{0}}^{{8}}}{f{{\left({x}\right)}}}{d}{x}={15}$$$ and $$${\int_{{5}}^{{8}}}{f{{\left({x}\right)}}}{d}{x}={11}$$$. Find $$${\int_{{0}}^{{5}}}{f{{\left({x}\right)}}}{d}{x}$$$.

Since $$${\int_{{0}}^{{8}}}{f{{\left({x}\right)}}}{d}{x}={\int_{{0}}^{{5}}}{f{{\left({x}\right)}}}{d}{x}+{\int_{{5}}^{{8}}}{f{{\left({x}\right)}}}{d}{x}$$$ then $$${15}={\int_{{0}}^{{5}}}{f{{\left({x}\right)}}}{d}{x}+{11}$$$.

So, $$${\int_{{0}}^{{5}}}{f{{\left({x}\right)}}}{d}{x}={4}$$$.

Constant Multiple Rule for Integrals: Constant can be factored out of integral sign: if is a constant then $$${\int_{{a}}^{{b}}}{k}{f{{\left({x}\right)}}}{d}{x}={k}{\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}$$$.

Sum (Difference) Rule for Integrals: $$${\int_{{a}}^{{b}}}{\left({f{{\left({x}\right)}}}\pm{g{{\left({x}\right)}}}\right)}{d}{x}={\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}\pm{\int_{{a}}^{{b}}}{g{{\left({x}\right)}}}{d}{x}$$$. Note that this rule is true for any number of functions.

Example 2. Use properties of integrals to evaluate $$${\int_{{-{1}}}^{{1}}}{\left({3}+{2}\sqrt{{{1}-{{x}}^{{2}}}}\right)}{d}{x}$$$

Using properties of integral we have that$$${\int_{{-{1}}}^{{1}}}{\left({3}+{2}\sqrt{{{1}-{{x}}^{{2}}}}\right)}{d}{x}={\int_{{-{1}}}^{{1}}}{3}{d}{x}+{\int_{{-{1}}}^{{1}}}{2}\sqrt{{{1}-{{x}}^{{2}}}}{d}{x}={\int_{{-{1}}}^{{1}}}{3}{d}{x}+{2}{\int_{{-{1}}}^{{1}}}\sqrt{{{1}-{{x}}^{{2}}}}{d}{x}=$$$

$$$={3}\cdot{\left({1}-{\left(-{1}\right)}\right)}+{2}\cdot\frac{\pi}{{2}}=\pi+{6}$$$

because $$${\int_{{-{1}}}^{{1}}}\sqrt{{{1}-{{x}}^{{2}}}}{d}{x}=\frac{\pi}{{2}}$$$ is area of semicircle with radius 1 and $$${\int_{{-{1}}}^{{1}}}{3}{d}{x}$$$ is area under line $$${y}={3}$$$ on interval $$${\left[-{1},{1}\right]}$$$ (clearly it is area of rectangle with sides 3 and $$${1}-{\left(-{1}\right)}={2}$$$).

Comparison Properties of Integrals
Comparison Property 1. If $$${f{{\left({x}\right)}}}\ge{0}$$$ for $$${a}\le{x}\le{b}$$$ then $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}\ge{0}$$$ (area under the graph of non-negative function should be non-negative).

Comparison Property 2. If $$${f{{\left({x}\right)}}}>{0}$$$ for $$${a}\le{x}\le{b}$$$ then $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}>{0}$$$ (area under the graph of positive function should be positive).

Comparison Property 3.If $$${f{{\left({x}\right)}}}\ge{g{{\left({x}\right)}}}$$$ for $$${a}\le{x}\le{b}$$$ then $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}\ge{\int_{{a}}^{{b}}}{g{{\left({x}\right)}}}{d}{x}$$$ (area under the graph of $$${f{}}$$$ should be bigger than area under the graph of $$${g{}}$$$ because $$${f{}}$$$ takes bigger values on all interval). This property follows from property 1 because $$${f{-}}{g{\ge}}{0}$$$.

Comparison Property 4. $$${\left|{\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}\right|}\le{\int_{{a}}^{{b}}}{\left|{f{{\left({x}\right)}}}\right|}{d}{x}$$$. Geometrically this means that absolute value of net area is not greater then sum of absolute values of areas. This inequality is very similar to triangle inequality $$${\left|{a}+{b}\right|}\le{\left|{a}\right|}+{\left|{b}\right|}$$$.

Comparison Property 5. If $$${m}\le{f{{\left({x}\right)}}}\le{M}$$$ for $$${a}\le{x}\le{b}$$$ then 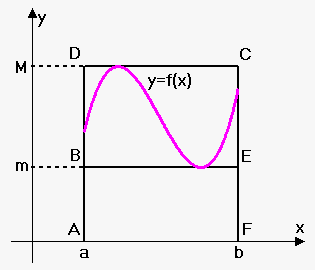comparison property of integral $$${m}{\left({b}-{a}\right)}\le{\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}\le{M}{\left({b}-{a}\right)}$$$. It says that if $$${m}$$$ is an absolute minimum and $$${M}$$$ is absolute maximum of $$${f{}}$$$ on interval $$${\left[{a},{b}\right]}$$$ then area under the graph of $$${f{}}$$$ is greater then area of rectangle with height $$${m}$$$ and lesser then area of rectangle with height $$${M}$$$. Looking on figure we can say that area under curve is less than area of rectangle ACDF and greater than area of rectangle ABEF. Note that this property gives very rough estimate.

Example 3. Use Comparison Property 5 to estimate $$${\int_{{1}}^{{2}}}\sqrt{{{{x}}^{{3}}+{1}}}{d}{x}$$$.

$$${f{{\left({x}\right)}}}=\sqrt{{{{x}}^{{3}}+{1}}}$$$ and $$${f{'}}{\left({x}\right)}=\frac{{1}}{{{2}\sqrt{{{{x}}^{{3}}+{1}}}}}\cdot{\left({{x}}^{{3}}+{1}\right)}'=\frac{{3}}{{2}}\frac{{{{x}}^{{2}}}}{{\sqrt{{{{x}}^{{3}}+{1}}}}}$$$.

As can be seen $$${f{'}}{\left({x}\right)}>{0}$$$ for all $$${x}$$$ on interval $$${\left[{1},{2}\right]}$$$, so $$${f{{\left({x}\right)}}}$$$ is increasing on interval $$${\left[{1},{2}\right]}$$$.

This means that on interval $$${\left[{1},{2}\right]}$$$ absolute minimum is $$${m}={f{{\left({1}\right)}}}=\sqrt{{{{1}}^{{3}}+{1}}}=\sqrt{{{2}}}$$$ and absolute maximum is $$${M}={f{{\left({2}\right)}}}=\sqrt{{{{2}}^{{3}}+{1}}}={3}$$$.

Therefore, $$$\sqrt{{{2}}}\cdot{\left({2}-{1}\right)}\le{\int_{{1}}^{{2}}}\sqrt{{{{x}}^{{3}}+{1}}}{d}{x}\le{3}\cdot{\left({2}-{1}\right)}$$$ or $$${1.414}\le{\int_{{1}}^{{2}}}\sqrt{{{{x}}^{{3}}+{1}}}{d}{x}\le{3}$$$.

Mean Value Theorem for Integrals. If $$${m}\le{f{{\left({x}\right)}}}\le{M}$$$ for $$${a}\le{x}\le{b}$$$ then there exists such number $$${n}$$$ that $$${m}\le{n}\le{M}$$$ and $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}={n}{\left({b}-{a}\right)}$$$.

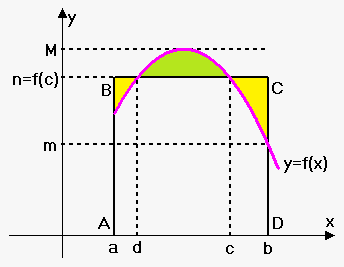mean value theorem for integrals Since $$${f{{\left({x}\right)}}}$$$ is continuous then equivalently there exists number $$${c}$$$ such that $$${a}\le{c}\le{b}$$$ and $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}={f{{\left({c}\right)}}}{\left({b}-{a}\right)}$$$.

Geometrically mean value theorem for positive functions means following: area under curve $$${y}={f{{\left({x}\right)}}}$$$ equals area of rectangle whose height lies somewhere between minimum and maximum values of $$${f{}}$$$ on interval $$${\left[{a},{b}\right]}$$$. In other words area under $$${f{{\left({x}\right)}}}$$$ equals area of rectangle ABCD (sum of yellow areas equals green area).

Note that there can be more than one point with above property. For example, on the figure there is another point $$${d}$$$ such that $$${n}={f{{\left({d}\right)}}}$$$.

Generalized Mean Value Theorem for Integrals. If $$${m}\le{f{{\left({x}\right)}}}\le{M}$$$ for $$${a}\le{x}\le{b}$$$ and $$${g{{\left({x}\right)}}}$$$ is either positive or negative on interval $$${\left[{a},{b}\right]}$$$ (in other words $$${g{{\left({x}\right)}}}$$$ doesn't change sign) then exists number $$${n}$$$ such that $$${m}\le{n}\le{M}$$$ and $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{g{{\left({x}\right)}}}{d}{x}={n}{\int_{{a}}^{{b}}}{g{{\left({x}\right)}}}{d}{x}$$$.

If $$${f{}}$$$ is continuous then we can equivalently write that there exists number $$${c}$$$ such that $$${a}\le{c}\le{b}$$$ and $$${\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{g{{\left({x}\right)}}}{d}{x}={f{{\left({c}\right)}}}{\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}$$$.