Maxima and Minima. Necessary Conditions
If function $$${y}={f{{\left({x}\right)}}}$$$ is defined and continuous on interval $$${\left[{a},{b}\right]}$$$ is not monotonic, then exist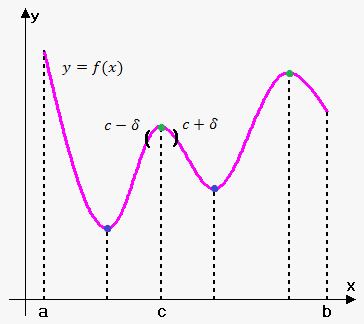 
such subintervals $$${\left[\alpha,\beta\right]}$$$ of interval $$${\left[{a},{b}\right]}$$$ that largest and smallest value function takes at inner point, i.e. between $$$\alpha$$$ and $$$\beta$$$.
Graphically such subintervals are represented as "humps" or "hollows".
Definition. It is said that function has at point $$${c}$$$ maximum (or minimum) if there exist such number $$$\delta>{0}$$$ that for all $$${x}\in{\left({c}-\delta,{c}+\delta\right)}$$$ we have that $$${f{{\left({x}\right)}}}\le{f{{\left({c}\right)}}}$$$ (or $$${f{{\left({x}\right)}}}\ge{f{{\left({c}\right)}}}$$$).
In other words there is maximum (minimum) at $$${c}$$$ if value $$${f{{\left({c}\right)}}}$$$ is the largest (smallest) among values that function can take in some neighborhood of $$${c}$$$.
This type of maximum (minimum) is sometimes called local or relative maximum (minimum) because function attains maximum (or minimum) in some small (local) interval.
Definition. Point $$${x}={c}$$$ is global or absolute maximum (minimum) of function $$${y}={f{{\left({x}\right)}}}$$$ if $$${f{{\left({c}\right)}}}\ge{f{{\left({x}\right)}}}$$$ $$$\left({f{{\left({c}\right)}}}\le{f{{\left({x}\right)}}}\right)$$$ for all $$${x}$$$ from the domain of $$${f{}}$$$.
Global maximum (minimum) is the largest (smallest) value the function can take over its domain.
It is clear that if maximum (minimum) is global then it is local.
We will call global and local maxima (minima) just maxima (minima).
Example 1. Functions $$${f{{\left({x}\right)}}}={\sin{{\left({x}\right)}}}$$$ takes its global (and local) maximum value of 1 infinitely many times, since $$${\sin{{\left({x}\right)}}}={1}$$$ for $$${x}=\frac{\pi}{{2}}+{2}\pi{n},{n}\in\mathbb{Z}$$$ and $$$-{1}\le{\sin{{\left({x}\right)}}}\le{1}$$$. Similarly, when $$${x}=-\frac{\pi}{{2}}+{2}\pi{m},{m}\in\mathbb{Z}$$$ sine takes its global (and local) minimum value of -1.
Example 2. If $$${f{{\left({x}\right)}}}={{x}}^{{2}}$$$ then $$${f{{\left({x}\right)}}}\ge{f{{\left({0}\right)}}}$$$ because $$${{x}}^{{2}}\ge{0}$$$ for all $$${x}$$$. Therefore, $$${x}={0}$$$ is the absolute (and local) minimum value of $$${f{}}$$$. However, there is no highest point on the parabola and so this function has no maximum value.
Example 3. $$${f{{\left({x}\right)}}}={{x}}^{{3}}$$$ has neither maximum values nor minimum values.
Example 4. Consider function $$${f{{\left({x}\right)}}}=\frac{{1}}{{3}}{{x}}^{{3}}-\frac{{3}}{{2}}{{x}}^{{2}}+{2}{x}$$$.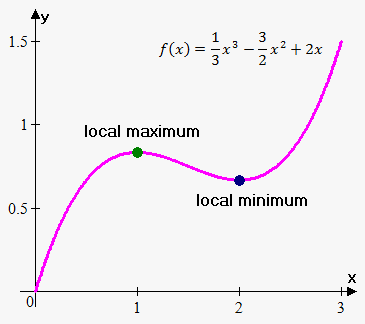
It has local minimum at $$${x}={2}$$$ and local maximum at $$${x}={1}$$$, but they are not global, because function grows without a bound as $$${x}\to\infty$$$ and decreases without a bound as $$${x}\to-\infty$$$. In fact there are no global maxima and minima.
However, if we change domain from $$${\left(-\infty,\infty\right)}$$$ to $$${\left[{1},{2}\right]}$$$ then $$${x}={2}$$$ becomes global minimum because there are no smaller values on interval $$${\left[{1},{2}\right]}$$$ then $$${f{{\left({2}\right)}}}$$$, and there are no larger values than $$${f{{\left({1}\right)}}}$$$ on interval $$${\left[{1},{2}\right]}$$$.
Definition. Extremum is a common name for maximum and minimum.
Definition. Point $$${c}$$$ from domain of $$${y}={f{{\left({x}\right)}}}$$$ is called stationary (or critical) point of function $$${y}={f{{\left({x}\right)}}}$$$ if $$${f{'}}{\left({c}\right)}={0}$$$ or $$${f{'}}{\left({c}\right)}$$$ doesn't exist (or infinite).
If point $$${c}$$$ is maximum or minimum then applying Fermat's Theorem to interval $$${\left({c}-\delta,{c}+\delta\right)}$$$ gives that $$${f{'}}{\left({c}\right)}={0}$$$.
This leads to the following fact.
Fact. Every extremum is a stationary point.
Converse is not true. Consider function $$${y}={{x}}^{{3}}$$$. Its derivative is $$${f{'}}{\left({x}\right)}={3}{{x}}^{{2}}$$$. Since $$${f{'}}{\left({0}\right)}={0}$$$ then point $$${x}={0}$$$ is stationary point, but it is clearly not an extremum.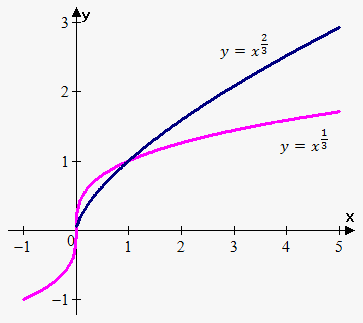
Above fact only tells us that if we want to find extrema we should start from finding stationary points and then somehow recognize which of them are indeed extrema.
Also if derivative at point $$${c}$$$ doesn't exist then point $$${c}$$$ in some cases is extremum and in some is not.
For example, derivative of function $$${f{{\left({x}\right)}}}={{x}}^{{\frac{{2}}{{3}}}}$$$ is $$${f{'}}{\left({x}\right)}=\frac{{2}}{{3}}\frac{{1}}{{{\sqrt[{{3}}]{{{x}}}}}}$$$. Clearly $$${f{'}}{\left({0}\right)}$$$ doesn't exist, but point $$${x}={0}$$$ is extremum.
Another example is $$${f{{\left({x}\right)}}}={\left|{x}\right|}$$$. Derivative doesn't exist at $$${x}={0}$$$, but $$${x}={0}$$$ is minimum.
For function $$${f{{\left({x}\right)}}}={{x}}^{{\frac{{1}}{{3}}}}$$$ derivative is $$${f{'}}{\left({x}\right)}=\frac{{1}}{{3}}\frac{{1}}{{{{x}}^{{\frac{{2}}{{3}}}}}}$$$. Clearly $$${f{'}}{\left({0}\right)}$$$ is infinite and $$${x}={0}$$$ is not extremum.
In the next sections we will identify extrema from stationary points.
Example 5. Find stationary points of $$${f{{\left({x}\right)}}}={2}{{x}}^{{3}}-{3}{{x}}^{{2}}-{12}{x}+{6}$$$.
First we find derivative $$${f{'}}{\left({x}\right)}={6}{{x}}^{{2}}-{6}{x}-{12}={6}{\left({{x}}^{{2}}-{x}-{2}\right)}={6}{\left({x}-{2}\right)}{\left({x}+{1}\right)}$$$.
Derivative is defined for all $$${x}$$$ so there are no points where derivative is infinite or doesn't exist.
So, we need to find points where derivative equals 0: $$${6}{\left({x}-{2}\right)}{\left({x}+{1}\right)}={0}$$$. From this we obtain that $$${x}={2}$$$ and $$${x}=-{1}$$$.
Therefore, there are two critical points: $$${x}={2}$$$ and $$${x}=-{1}$$$.
Example 6. Find stationary points of $$${f{{\left({x}\right)}}}=\frac{{{{x}}^{{2}}+{3}}}{{{x}-{1}}}$$$.
First we find derivative $$${f{'}}{\left({x}\right)}=\frac{{{\left({{x}}^{{2}}+{3}\right)}'{\left({x}-{1}\right)}-{\left({{x}}^{{2}}+{3}\right)}{\left({x}-{1}\right)}'}}{{{\left({x}-{1}\right)}}^{{2}}}=\frac{{{{x}}^{{2}}-{2}{x}-{3}}}{{{\left({x}-{1}\right)}}^{{2}}}=\frac{{{\left({x}-{3}\right)}{\left({x}+{1}\right)}}}{{{x}-{1}}}$$$.
Derivative is defined for all $$${x}$$$ except $$${x}={1}$$$, but at this point function is also not defined. So $$${x}={1}$$$ is not stationary point.
So, we need to find points where derivative equals 0: $$$\frac{{{\left({x}-{3}\right)}{\left({x}+{1}\right)}}}{{{x}-{1}}}={0}$$$. From this we obtain that $$${x}={3}$$$ and $$${x}=-{1}$$$.
Therefore, there are two critical points: $$${x}={3}$$$ and $$${x}=-{1}$$$.
Example 7. Find stationary points of $$${f{{\left({x}\right)}}}={x}\sqrt{{{x}-{1}}}$$$.
First we find derivative $$${f{'}}{\left({x}\right)}={x}'\sqrt{{{x}-{1}}}+{x}{\left(\sqrt{{{x}-{1}}}\right)}'=\sqrt{{{x}-{1}}}+\frac{{x}}{{{2}\sqrt{{{x}-{1}}}}}=\frac{{{3}{x}-{2}}}{{{2}\sqrt{{{x}-{1}}}}}$$$.
Derivative is defined for all $$${x}$$$ except $$${x}={1}$$$. Since functions is defined when $$${x}={1}$$$ so $$${x}={1}$$$ is critical point.
Now, we need to find points where derivative equals 0: $$$\frac{{{3}{x}-{2}}}{{{2}\sqrt{{{x}-{1}}}}}={0}$$$. From this we obtain that $$${x}=\frac{{2}}{{3}}$$$.
Therefore, there are two critical points: $$${x}=\frac{{2}}{{3}}$$$ and $$${x}={1}$$$.