Condition of Monotony of the Function
Now let's formulate conditions when function will be monotonic, i.e. increasing, decreasing, non-decreasing, non-increasing.
Fact 1. Suppose function $$${y}={f{{\left({x}\right)}}}$$$ is defined and continuous on interval $$${X}$$$ and has finite derivative $$${f{'}}{\left({x}\right)}$$$ on it. Then function is non-decreasing (non-increasing) on $$${X}$$$ if and only if $$${f{'}}{\left({x}\right)}\ge{0}$$$ $$$\left({f{'}}{\left({x}\right)}\le{0}\right)$$$ for all $$${x}$$$ in $$${X}$$$.
This fact doesn't exclude the possibility that functon will be constant on some intervals.
Next fact will exclude this posibility.
Fact 2. Suppose function $$${y}={f{{\left({x}\right)}}}$$$ is defined and continuous on interval $$${X}$$$ and has finite derivative $$${f{'}}{\left({x}\right)}$$$ on it. Then function is increasing (decreasing) on $$${X}$$$ if and only if $$${f{'}}{\left({x}\right)}\ge{0}$$$ $$$\left({f{'}}{\left({x}\right)}\le{0}\right)$$$ for all $$${x}$$$ in $$${X}$$$ and $$${f{'}}{\left({x}\right)}$$$ is not 0 on any subinterval of $$${X}$$$.
Notice that the only difference between Fact 1 and Fact 2 is phrase: "$$${f{'}}{\left({x}\right)}$$$ is not 0 on any subinterval of $$${X}$$$". Adding this condition guarantees that function is not constant on some subinterval of $$${X}$$$.
Connection between sign of derivative and direction of change of function is geometrically obvious. Recall that derivative is slope of tangent line. Function is increasing when slope of tangent line is positive, and decreasing if slope of tangent line is negative.
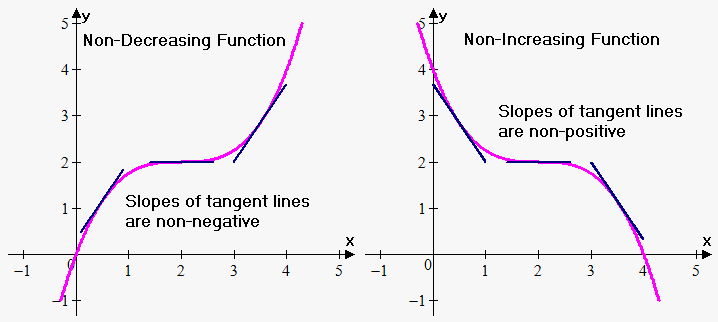
However, at some points tangent line can be horizontal, i.e. derivative of increasing (decreasing) function can equal 0 at some points.
For example, consider function $$${y}={{x}}^{{3}}$$$. It is increasing, but $$${f{'}}{\left({x}\right)}={3}{{x}}^{{2}}$$$ equals 0 when $$${x}={0}$$$.
Another example is increasing function $$${f{{\left({x}\right)}}}={x}-{\sin{{\left({x}\right)}}}$$$. Its derivative $$${f{'}}{\left({x}\right)}={1}-{\cos{{\left({x}\right)}}}$$$ is non-negative and equals 0 when $$${x}={2}\pi{k},{k}\in{Z}$$$.
As we saw function will be still increasing (decreasing) even if its derivative is non-negative (non-positive) and equals 0 at some points.
But if derivative is non-negative (or non-positive) on $$${X}$$$ and equals 0 on some subinterval of $$${X}$$$ then function will be non-decreasing (non-increasing).
Example 1. Find where function $$${f{{\left({x}\right)}}}={{x}}^{{3}}+\frac{{15}}{{2}}{{x}}^{{2}}+{12}{x}+{5}$$$ is increasing and decreasing.
$$${f{'}}{\left({x}\right)}={3}{{x}}^{{2}}+{15}{x}+{12}={3}{\left({{x}}^{{2}}+{5}{x}+{4}\right)}={3}{\left({x}+{4}\right)}{\left({x}+{1}\right)}$$$. We need to know where $$${f{'}}{\left({x}\right)}>{0}$$$ and where $$${f{'}}{\left({x}\right)}<{0}$$$.
For this we use method of intervals.
To do this divide real line into intervals whose endpoints are values where $$${f{'}}{\left({x}\right)}={0}$$$: -4 and -1.
First interval is $$${\left(-\infty,-{4}\right)}$$$: here $$${x}+{4}<{0}$$$ and $$${x}+{1}<{0}$$$ so $$${f{'}}{\left({x}\right)}>{0}$$$.
Second interval is $$${\left(-{4},-{1}\right)}$$$: here $$${x}+{4}>{0}$$$ and $$${x}+{1}<{0}$$$ so $$${f{'}}{\left({x}\right)}<{0}$$$.
Third interval is $$${\left(-{1},\infty\right)}$$$: here $$${x}+{4}>{0}$$$ and $$${x}+{1}>{0}$$$ so $$${f{'}}{\left({x}\right)}>{0}$$$.
Therefore function is increasing on $$${\left(-\infty,-{4}\right)}\cup{\left(-{1},\infty\right)}$$$ and decreasing on $$${\left(-{4},-{1}\right)}$$$.
Example 2. Find intervals of monotony of function $$${f{{\left({x}\right)}}}=\frac{{{x}+{2}}}{{{{x}}^{{2}}-{3}}}$$$.
Using Quotient Rule we obtain that $$${f{'}}{\left({x}\right)}=\frac{{{\left({x}+{2}\right)}'{\left({{x}}^{{2}}-{3}\right)}-{\left({x}+{2}\right)}{\left({{x}}^{{2}}-{3}\right)}'}}{{{{\left({{x}}^{{2}}-{3}\right)}}^{{2}}}}=\frac{{{{x}}^{{2}}-{3}-{2}{{x}}^{{2}}-{4}{x}}}{{{\left({{x}}^{{2}}-{3}\right)}}^{{2}}}=-\frac{{{{x}}^{{2}}+{4}{x}+{3}}}{{{\left({{x}}^{{2}}-{3}\right)}}^{{2}}}=-\frac{{{\left({x}+{1}\right)}{\left({x}+{3}\right)}}}{{{\left({{x}}^{{2}}-{3}\right)}}^{{2}}}$$$.
Again we use method of intervals.
Note, that denominator is always non-negative and thus doesn't influence sign of derivative, so ignore it.
Divide real line into intervals whose endpoints are values where $$${f{'}}{\left({x}\right)}={0}$$$: -3 and -1.
First interval is $$${\left(-\infty,-{3}\right)}$$$: here $$${x}+{3}<{0}$$$ and $$${x}+{1}<{0}$$$ so $$${f{'}}{\left({x}\right)}=-{\left({x}+{1}\right)}{\left({x}+{3}\right)}<{0}$$$.
Second interval is $$${\left(-{3},-{1}\right)}$$$: here $$${x}+{3}>{0}$$$ and $$${x}+{1}<{0}$$$ so $$${f{'}}{\left({x}\right)}=-{\left({x}+{1}\right)}{\left({x}+{3}\right)}>{0}$$$.
Third interval is $$${\left(-{1},\infty\right)}$$$: here $$${x}+{3}>{0}$$$ and $$${x}+{1}>{0}$$$ so $$${f{'}}{\left({x}\right)}=-{\left({x}+{1}\right)}{\left({x}+{3}\right)}<{0}$$$.
Therefore function is increasing on $$${\left(-{3},-{1}\right)}$$$ and decreasing on $$${\left(-\infty,-{3}\right)}\cup{\left(-{1},\infty\right)}$$$.
Example 3. Find where function $$${f{{\left({x}\right)}}}=\frac{{1}}{{4}}{{x}}^{{4}}-\frac{{1}}{{3}}{{x}}^{{3}}+{2}$$$ is increasing and where is decreasing.
We have that $$${f{'}}{\left({x}\right)}={{x}}^{{3}}-{{x}}^{{2}}={{x}}^{{2}}{\left({x}-{1}\right)}$$$.
$$${{x}}^{{2}}$$$ is always non-negative and doesn't influence sign of derivative. So, function is increasing when $$${x}>{1}$$$ and decreasing when $$${x}<{1}$$$.
