Tangent Line, Velocity, and Other Rates of Changes
Now we are going to talk about the problems that lead to the concept of derivative.
The Tangent Line
Suppose that we are given a curve $$$y={f{{\left({x}\right)}}}$$$ and a point on the curve $$${P}{\left({a},{f{{\left({a}\right)}}}\right)}$$$. We want to find the equation of the tangent line at the point $$$P$$$.
The word "tangent" means "touching"; so, we need to find a line that touches the curve and is parallel (in some sense) to the curve at the point of intersection.
But this is a verbal description. We need to state a formal definition.
So, how do we find the equation of the tangent line at the point $$${P}{\left({a},{f{{\left({a}\right)}}}\right)}$$$?
To find the equation of any line, we need two points. Here, we have only one point, namely $$${\left({a},{f{{\left({a}\right)}}}\right)}$$$. However, we can take a point $$$Q$$$ and find the equation of the line passing through the points $$$P$$$ and $$$Q$$$.
Let's see how this is done.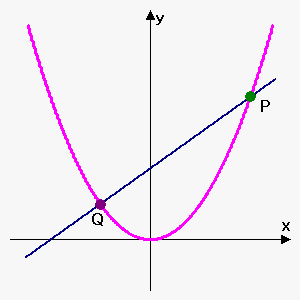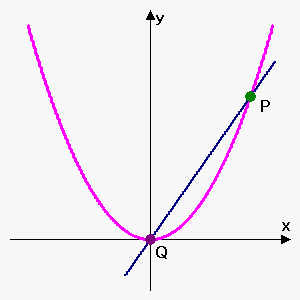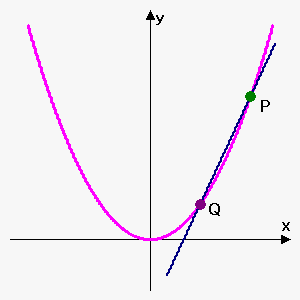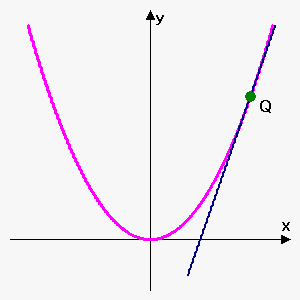
Let's assume that the point $$$Q$$$ has the coordinates $$${\left({b},{f{{\left({b}\right)}}}\right)}$$$ and the equation of the tangent line is $$${y}={m}{x}+{c}$$$, where $$${m}$$$ and $$${c}$$$ are to be determined.
Then, the slope of the line that passes through the points $$${P}$$$ and $$${Q}$$$ is $$${m}=\frac{{{f{{\left({b}\right)}}}-{f{{\left({a}\right)}}}}}{{{b}-{a}}}$$$.
If we move the point $$${Q}$$$ towards the point $$${P}$$$ along the curve $$${y}={f{{\left({x}\right)}}}$$$, we will obtain the tangent line as $$${Q}$$$ becomes very close to $$${P}$$$. We say that the slope of the tangent line is the limit of the slopes of all lines through $$$P$$$ and $$$Q$$$ when $$$Q$$$ approaches $$$P$$$. In other words, the slope of the tangent line is $$${m}=\lim_{{{b}\to{a}}}\frac{{{f{{\left({b}\right)}}}-{f{{\left({a}\right)}}}}}{{{b}-{a}}}$$$.
It doesn't matter whether the point $$${Q}$$$ approaches $$${P}$$$ from the left or from the right.
If we now set $$${b}={a}+{h}$$$, given the fact that $$${b}\to{a}$$$, we have that $$${h}\to{0}$$$.
Now, the slope of the tangent line can be rewritten as $$${m}=\lim_{{{h}\to{0}}}\frac{{{f{{\left({a}+{h}\right)}}}-{f{{\left({a}\right)}}}}}{{h}}$$$.
But this is the derivative at the point $$${a}$$$. So, $$${m}={f{'}}{\left({a}\right)}$$$.
Thus, we have the following fact:
Fact. The equation of the tangent line to the curve $$${y}={f{{\left({x}\right)}}}$$$ at the point $$${a}$$$ is $$${y}={f{{\left({a}\right)}}}+{f{'}}{\left({a}\right)}{\left({x}-{a}\right)}$$$.
Now, let's see how the tangent line can be found in practice.
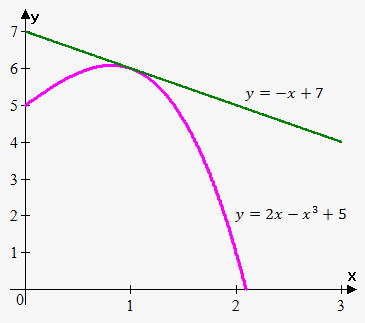 Example 1. Find the equation of the tangent line to $$${y}={2}{x}-{{x}}^{{3}}+{5}$$$ at the point $$${P}={\left({1},{6}\right)}$$$.
Example 1. Find the equation of the tangent line to $$${y}={2}{x}-{{x}}^{{3}}+{5}$$$ at the point $$${P}={\left({1},{6}\right)}$$$.
We have that $$${f{{\left({x}\right)}}}={2}{x}-{{x}}^{{3}}+{5}$$$.
Therefore, $$${f{'}}{\left({x}\right)}={2}-{3}{{x}}^{{2}}$$$, and $$${f{'}}{\left({1}\right)}={2}-{3}\cdot{{1}}^{{2}}=-{1}$$$.
Thus, the equation of the tangent line is $$${y}={6}+{\left(-{1}\right)}{\left({x}-{1}\right)}$$$ or $$${y}=-{x}+{7}$$$.
The Velocity Problem
Consider the object that is dropped from height (we neglect air resistance).
Galileo discovered that the distance traveled by this object is $$${s}=\frac{{g}}{{2}}{{t}}^{{2}}$$$, where $$${g{=}}{9.81}\frac{{m}}{{{s}}^{{2}}}$$$ is constant.
First, consider the case when we want to find the average velocity. It is known that the average velocity is the distance traveled divided by the time needed to travel that distance.
For example, let's find the average velocity from $$${t}={1}$$$ to $$${t}={5}$$$ seconds: $$${v}_{{{a}{v}{e}}}=\frac{{{s}{\left({5}\right)}-{s}{\left({1}\right)}}}{{{5}-{1}}}=\frac{{\frac{{9.81}}{{2}}\cdot{{5}}^{{2}}-\frac{{9.81}}{{2}}\cdot{{1}}^{{2}}}}{{4}}={3}\cdot{9.81}={29.43}\frac{{m}}{{s}}$$$.
But what if we want to find the velocity at some particular time? What if we want to find the instantaneous velocity?
In this case, we don't have the time interval and thus we can't find the average velocity. However, let's take the interval $$${\left[{t},{t}+{h}\right]}$$$: the average velocity is $$${v}=\frac{{{s}{\left({t}+{h}\right)}-{s}{\left({t}\right)}}}{{{t}+{h}-{t}}}=\frac{{{s}{\left({t}+{h}\right)}-{s}{\left({t}\right)}}}{{h}}$$$. If we now let $$${h}\to{0}$$$, we will make the interval $$${\left[{t},{t}+{h}\right]}$$$ very small and thus will find the instantaneous velocity: $$${v}=\lim_{{{h}\to{0}}}\frac{{{s}{\left({t}+{h}\right)}-{s}{\left({t}\right)}}}{{h}}$$$. But this is again the derivative of the function $$${s}{\left({t}\right)}$$$ with respect to time.
So, $$${s}'{\left({t}\right)}={\left(\frac{{g}}{{2}}{{t}}^{{2}}\right)}'=\frac{{g}}{{2}}\cdot{2}{t}={g{{t}}}={9.81}{t}$$$, and, for example, the instantaneous velocity at the time $$${t}={3}$$$ is $$${s}'{\left({3}\right)}={9.81}\cdot{3}={29.43}\frac{{m}}{{s}}$$$.
In general, suppose that an object is moving along a straight line according to the equation of motion $$${s}={f{{\left({t}\right)}}}$$$, where $$${s}$$$ is the displacement (directed distance) of the object from the origin at the time $$${t}$$$. The function $$${f{}}$$$ that describes the motion is called the position function.
Fact. Velocity is the derivative of the position function: $$${v}={s}'$$$.
Example 2. Suppose that a distance a car traveled at any time $$${t}$$$ is given as $$${s}{\left({t}\right)}={{t}}^{{2}}+{t}+{5}$$$ meters. This means that, for example, after $$$2$$$ seconds, the car travelled $$${{2}}^{{2}}+{2}+{5}={11}$$$ meters. Find the velocity of the car after $$$4$$$ seconds.
Since the velocity of the car is the derivative of the position function, we have that $$${v}{\left({t}\right)}={s}'{\left({t}\right)}$$$: $$${v}{\left({t}\right)}={\left({{t}}^{{2}}+{t}+{5}\right)}'={\left({{t}}^{{2}}\right)}+{\left({t}\right)}'+{\left({5}\right)}'={2}{t}+{1}$$$.
Thus, the velocity of the car after $$$4$$$ seconds is $$${v}{\left({4}\right)}={2}\cdot{4}+{1}={9}\frac{{m}}{{s}}$$$.
Note how close the tangent and the velocity problems are. In both cases, we need to find some quantity at a point. To do this, we take an interval and then shorten it to the limiting value (with the tangent problems, it is the length of the line through $$$P$$$ and $$$Q$$$, and with the velocity problem – the time interval).
In fact, we can extend this idea to any problem.
Suppose that we are given a function $$${y}={f{{\left({x}\right)}}}$$$. On the interval $$${\left[{x}_{{1}},{x}_{{2}}\right]}$$$, the change in $$${x}$$$ is $$$\Delta{x}={x}_{{2}}-{x}_{{1}}$$$, and the corresponding change in $$${y}$$$ is $$$\Delta{y}={y}_{{2}}-{y}_{{1}}$$$.
Then, the rate of change of $$${y}$$$ with respect to $$${x}$$$ is $$$\frac{{\Delta{y}}}{{\Delta{x}}}=\frac{{{y}_{{2}}-{y}_{{1}}}}{{{x}_{{2}}-{x}_{{1}}}}=\frac{{{f{{\left({x}_{{2}}\right)}}}-{f{{\left({x}_{{1}}\right)}}}}}{{{x}_{{2}}-{x}_{{1}}}}$$$.
The instantaneous rate of change is $$$\lim_{{\Delta{x}\to{0}}}\frac{{\Delta{y}}}{{\Delta{x}}}=\lim_{{\Delta{x}\to{0}}}\frac{{{f{{\left({x}_{{2}}\right)}}}-{f{{\left({x}_{{1}}\right)}}}}}{{{x}_{{2}}-{x}_{{1}}}}$$$.
But we recognize in this the limit derivative. Indeed, if we set $$${x}_{{2}}-{x}_{{1}}={h}$$$, we have that $$${h}\to{0}$$$ as $$$\Delta{x}\to{0}$$$ and $$${x}_{{2}}={x}_{{1}}+{h}$$$.
Now, the instantaneous rate of change can be rewritten as $$$\lim_{{{h}\to{0}}}\frac{{{f{{\left({x}_{{1}}+{h}\right)}}}-{f{{\left({x}_{{1}}\right)}}}}}{{h}}$$$, which is the derivative at the point $$${x}_{{1}}$$$.
Fact. The derivative $$${f{'}}{\left({a}\right)}$$$ is the instantaneous rate of change of $$${y}={f{{\left({x}\right)}}}$$$ with respect to $$${x}$$$ when $$${x}={a}$$$.
For example, suppose that $$${N}{\left({t}\right)}$$$ is a population of bacteria at any time $$${t}$$$. Then, $$${N}'{\left({t}\right)}$$$ is the rate of change of the population at any given time $$${t}$$$, i.e. it expresses how fast the population is changing at any time $$${t}$$$.
Example 3. Suppose that a population of bacteria at any time $$${t}$$$ ($$${t}$$$ is measured in hours) is $$${N}{\left({t}\right)}={100}{{e}}^{{t}}+{2}{{t}}^{{2}}$$$. How fast is the population increasing after two hours?
We need to find $$${f{'}}{\left({2}\right)}$$$. Since $$${N}'{\left({t}\right)}={100}{{e}}^{{t}}+{4}{t}$$$, we have that $$${N}'{\left({2}\right)}={100}\cdot{{e}}^{{2}}+{4}\cdot{2}\approx{747}$$$ bacteria per hour.
So, after two hours, the population of bacteria is growing at a rate of $$$747$$$ bacteria per hour.
