Studying Derivative Graphically
In this note, we are going to talk about how to sketch the graph of the derivative knowing the graph of the function and see graphically when the function is not differentiable.
Example. The graph of the function is shown. Sketch the graph of the derivative.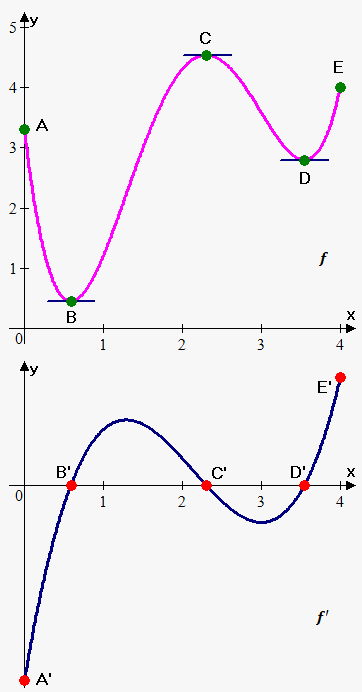
We know that the derivative at some point is the slope of the tangent line at that point.
Therefore, by calculating the slope of the tangent lines at different points, we will be able to sketch the graph of the derivative.
From $$$A$$$ to $$$B$$$, the slopes are negative; so, the derivative will be negative on this interval.
From $$$B$$$ to $$$C$$$, the slopes are positive; so, the derivative is positive here.
Similarly, it can be found that the derivative is negative from $$$C$$$ to $$$D$$$ and positive from $$$D$$$ to $$$E$$$.
Note that at the points $$$B$$$, $$$C$$$, and $$$D$$$, the tangent lines are horizontal; thus, their slope is $$$0$$$.
So, the value of the derivative at these points is $$$0$$$.
Now, let's see when the function is not differentiable.
We know that when the function is differentiable, it is continuous.
From this, we can draw a conclusion that if the function is discontinuous, it is not differentiable.
The other two cases are when the derivative is infinite (the tangent line is vertical) or the derivative doesn't exist (the one-sided limits are not equal). The latter case means that the graph of the function has a "corner," in other words, the direction changes abruptly as the graph of the function $$$y={\left|{x}\right|}$$$ at $$$x=0$$$.
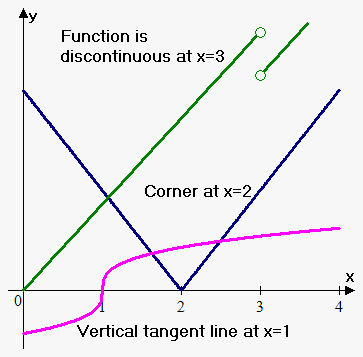 So, the function is not differentiable at $$$x=a$$$ when one of the following holds:
So, the function is not differentiable at $$$x=a$$$ when one of the following holds:
- the function is not continuous at $$${x}={a}$$$;
- the derivative at the point $$${a}$$$ is infinite (vertical tangent line);
- there is a corner at the point $$${a}$$$ (the one-sided limits exist but they are not equal).
All the three cases are shown on the figure.
