First Derivative Test
We know that if point is extremum then it is stationary point. So, we need to find all stationary points and test them. But how?
For this we use following test.
First Derivative Test. Suppose that $$${c}$$$ is a stationary point of a continuous function $$${y}={f{{\left({x}\right)}}}$$$.
- if $$${f{'}}{\left({x}\right)}$$$ changes sign from negative to positive at $$${c}$$$, then $$${f{{\left({x}\right)}}}$$$ has minimum at $$${c}$$$.
- if $$${f{'}}{\left({x}\right)}$$$ changes sign from positive to negative at $$${c}$$$, then $$${f{{\left({x}\right)}}}$$$ has maximum at $$${c}$$$.
- if $$${f{'}}{\left({x}\right)}$$$ doesn't change sign at $$${c}$$$, (in other words derivative is either positive or negative on both sides of $$${c}$$$) then $$${f{{\left({x}\right)}}}$$$ has neither minimum nor maximum at $$${c}$$$.
From geometrical point of view first derivative test is very clear. If function is increasing $$${\left({f{'}}{\left({x}\right)}>{0}\right)}$$$ to point $$${c}$$$ and then decreasing $$$\left({f{{\left({x}\right)}}}<{0}\right)$$$, then there is maximum at $$${c}$$$. Similarly for minimum. From the other side if function is increasing (decreasing) before and after point $$${c}$$$ then clearly there is no maximum or minimum.

Now it is clear why $$${f{{\left({x}\right)}}}={{x}}^{{3}}$$$ doesn't have extremum at $$${x}={0}$$$. Because $$${f{'}}{\left({x}\right)}={3}{{x}}^{{2}}$$$ doesn't change sign at $$${x}={0}$$$.
Example 1. Find and classify extrema of $$${f{{\left({x}\right)}}}={3}{{x}}^{{4}}-{4}{{x}}^{{3}}-{12}{{x}}^{{2}}+{1}$$$.
$$${f{'}}{\left({x}\right)}={12}{{x}}^{{3}}-{12}{{x}}^{{2}}-{24}{x}={12}{x}{\left({{x}}^{{2}}-{x}-{2}\right)}={12}{x}{\left({x}-{2}\right)}{\left({x}+{1}\right)}$$$.
So, the critical points are $$${x}={0}$$$, $$${x}={2}$$$ and $$${x}=-{1}$$$.
To find type of stationary point (maximum minimum or neither) we need to find sign of derivative. We again use method of intervals: divide real line into intervals whose endpoints are stationary points: $$${\left(-\infty,-{1}\right)},{\left(-{1},{0}\right)},{\left({0},{2}\right)},{\left({2},\infty\right)}$$$.
First interval is $$${\left(-\infty,-{1}\right)}$$$: here $$${x}+{1}<{0}$$$, $$${x}<{0}$$$ and $$${x}-{2}<{0}$$$ therefore $$${f{'}}{\left({x}\right)}<{0}$$$.
Second interval is $$${\left(-{1},{0}\right)}$$$: here $$${x}+{1}>{0}$$$, $$${x}<{0}$$$ and $$${x}-{2}<{0}$$$ therefore $$${f{'}}{\left({x}\right)}>{0}$$$.
Third interval is $$${\left({0},{2}\right)}$$$: here $$${x}+{1}>{0}$$$, $$${x}>{0}$$$ and $$${x}-{2}<{0}$$$ therefore $$${f{'}}{\left({x}\right)}<{0}$$$.
Fourth interval is $$${\left({2},\infty\right)}$$$: here $$${x}+{1}>{0}$$$, $$${x}>{0}$$$ and $$${x}-{2}>{0}$$$ therefore $$${f{'}}{\left({x}\right)}>{0}$$$.
Now, examine critical points:
$$${x}=-{1}$$$; derivative changes sign from negative to positive therefore $$${x}=-{1}$$$ is minimum.
$$${x}={0}$$$; derivative changes sign from positive to negative therefore $$${x}={0}$$$ is maximum.
$$${x}={2}$$$; derivative changes sign from negative to positive therefore $$${x}={2}$$$ is minimum.
Example 2. Find maxima and minima of $$${f{{\left({x}\right)}}}={{\left({x}+{2}\right)}}^{{2}}{{\left({x}-{1}\right)}}^{{3}}$$$.
Deivative of function is defined and exist for all $$${x}$$$:
$$${f{'}}{\left({x}\right)}={2}{\left({x}+{2}\right)}{{\left({x}-{1}\right)}}^{{3}}+{3}{{\left({x}+{2}\right)}}^{{2}}{{\left({x}-{1}\right)}}^{{2}}={\left({x}+{2}\right)}{{\left({x}-{1}\right)}}^{{2}}{\left({2}{x}-{2}+{3}{x}+{6}\right)}=$$$
$$$={\left({x}+{2}\right)}{{\left({x}-{1}\right)}}^{{2}}{\left({5}{x}-{4}\right)}={5}{\left({x}+{2}\right)}{{\left({x}-{1}\right)}}^{{2}}{\left({x}-\frac{{4}}{{5}}\right)}$$$.
So, the stationary points (roots of derivative) are $$${x}=-{2}$$$, $$${x}={1}$$$ and $$${x}=\frac{{4}}{{5}}$$$.
We again use method of intervals: divide real line into intervals whose endpoints are stationary points: $$${\left(-\infty,-{2}\right)},{\left(-{2},\frac{{4}}{{5}}\right)},{\left(\frac{{4}}{{5}},{1}\right)},{\left({1},\infty\right)}$$$.
First interval is $$${\left(-\infty,-{2}\right)}$$$: here $$${x}+{2}<{0}$$$, $$${{\left({x}-{1}\right)}}^{{2}}>{0}$$$ and $$${x}-\frac{{4}}{{5}}<{0}$$$ therefore $$${f{'}}{\left({x}\right)}>{0}$$$.
Second interval is $$${\left(-{2},\frac{{4}}{{5}}\right)}$$$: here $$${x}+{2}>{0}$$$, $$${{\left({x}-{1}\right)}}^{{2}}>{0}$$$ and $$${x}-\frac{{4}}{{5}}<{0}$$$ therefore $$${f{'}}{\left({x}\right)}<{0}$$$.
Third interval is $$${\left(\frac{{4}}{{5}},{1}\right)}$$$: here $$${x}+{2}>{0}$$$, $$${{\left({x}-{1}\right)}}^{{2}}>{0}$$$ and $$${x}-\frac{{4}}{{5}}>{0}$$$ therefore $$${f{'}}{\left({x}\right)}>{0}$$$.
Fourth interval is $$${\left({1},\infty\right)}$$$: here $$${x}+{2}>{0}$$$, $$${{\left({x}-{1}\right)}}^{{2}}>{0}$$$ and $$${x}-\frac{{4}}{{5}}>{0}$$$ therefore $$${f{'}}{\left({x}\right)}>{0}$$$.
Now, examine critical points:
$$${x}=-{2}$$$; derivative changes sign from positive to negative therefore $$${x}=-{2}$$$ is maximum.
$$${x}=\frac{{4}}{{5}}$$$; derivative changes sign from negative to positive therefore $$${x}=\frac{{4}}{{5}}$$$ is minimum.
$$${x}={2}$$$; derivative doesn't change sign (it is positive on both sides of $$${x}={2}$$$) therefore $$${x}={2}$$$ is neither minimum nor maximum.
Now, we can easily calculate maximum and minimum values: $$${f{{\left(-{2}\right)}}}={0}$$$, $$${f{{\left(-\frac{{4}}{{5}}\right)}}}=-{8.4}$$$.
Example 3. Find extrema of the function $$${y}={{\sin}}^{{3}}{\left({x}\right)}+{{\cos}}^{{3}}{\left({x}\right)}$$$.
Since function is periodic with period $$${2}\pi$$$ we will consider only interval $$${\left[{0},{2}\pi\right]}$$$.
Derivative is $$${f{'}}{\left({x}\right)}={3}{{\sin}}^{{2}}{\left({x}\right)}{\cos{{\left({x}\right)}}}+{3}{{\cos}}^{{2}}{\left({x}\right)}{\left(-{\sin{{\left({x}\right)}}}\right)}={3}{\sin{{\left({x}\right)}}}{\cos{{\left({x}\right)}}}{\left({\sin{{\left({x}\right)}}}-{\cos{{\left({x}\right)}}}\right)}$$$.
On interval $$${\left[{0},{2}\pi\right]}$$$ $$${\sin{{\left({x}\right)}}}={0}$$$ when $$${x}={0},\pi,{2}\pi$$$, $$${\cos{{\left({x}\right)}}}={0}$$$ when $$${x}=\frac{\pi}{{2}},\frac{{{3}\pi}}{{2}}$$$.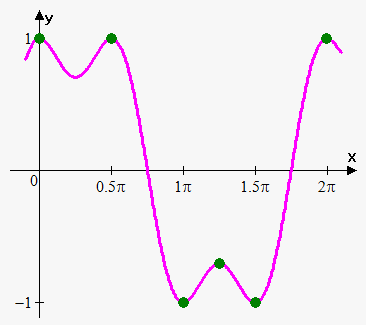
To solve equation $$${\sin{{\left({x}\right)}}}-{\cos{{\left({x}\right)}}}={0}$$$ we divide both sides by $$${\cos{{\left({x}\right)}}}$$$ ($$${\cos{{\left({x}\right)}}}\ne{0}$$$ because we already considered that case): $$${\tan{{\left({x}\right)}}}={1}$$$ or $$${x}=\frac{\pi}{{4}},\frac{{{5}\pi}}{{4}}$$$.
So, stationary points are $$${x}={0},\frac{\pi}{{4}},\frac{\pi}{{2}},\pi,\frac{{{5}\pi}}{{4}},\frac{{{3}\pi}}{{2}},{2}\pi$$$.
Using method of intervals we see that stationary points by turns attain maximum and minimum of function.
Maxima: $$${f{{\left({0}\right)}}}={f{{\left(\frac{\pi}{{2}}\right)}}}={f{{\left({2}\pi\right)}}}={1}$$$, $$${f{{\left(\frac{{{5}\pi}}{{4}}\right)}}}=-\frac{\sqrt{{{2}}}}{{2}}$$$. Note that $$${0},\frac{\pi}{{2}},{2}\pi$$$ are global maxima while $$$\frac{{{5}\pi}}{{4}}$$$ is local.
Minima: $$${f{{\left(\frac{\pi}{{4}}\right)}}}=\frac{\sqrt{{{2}}}}{{2}}$$$, $$${f{{\left(\pi\right)}}}={f{{\left(\frac{{{3}\pi}}{{2}}\right)}}}=-{1}$$$. Note that $$$\pi,\frac{{{3}\pi}}{{2}}$$$ are global minima while $$$\frac{\pi}{{4}}$$$ is local.
