Steps for Sketching the Graph of the Function
Related Calculator: MathGrapher: Graphing Calculator-Function Grapher
Suppose we are given continuous on `[a,b]` function `y=f(x)` that is twice differentiable, except points where derivative `f'(x)` doesn't exist or has infinite value.
To sketch the graph of the function, we need to perform the following:
- Determine, whether function is obtained by transforming a simpler function, and perform necessary steps for this simpler function.
- Determine, whether function is even, odd or periodic. This allows to draw graph of the function on some subinterval and then just reflect the result.
- Find y-intercept (point `f(0)`).
- Find x-intercepts (points where `f(x)=0`).
- Find what asymptotes does function have, if any.
- Calculate first derivative and find points where `f'(x)=0` or `f'(x)` doesn't exist, in other words find stationary points.
- Use test (First Derivative or Second Derivative) to classify stationary points.
- Find intervals where function is increasing (`f'(x)>0`) and where it is decreasing (`f'(x)<0`).
- Find points where `f''(x)=0` or `f''(x)` doesn't exist and test whether these points are points of inflection.
- Find where function is concave up (`f''(x)>0`) and where it is concave down (`f''(x)<0`).
- After you've found "important" points calculate corresponding values of function at these points.
- Add "control" points (some arbitrary points), if needed.
- Draw "important" and "control" points and connect them by lines taking into account found behavior of the function.
- If function is even, odd or periodic then perform corresponding reflection.
- If function is obtained by transforming simpler function, perform corresponding shift, compressing/stretching.
It is often convenient to draw all points, you've found, in the table.
Example 1. Sketch graph of the function `f(x)=1/(x-1)`.
Since `f(x)=g(x-1)` where `g(x)=1/x` then we study function `g(x)=1/x` and then shift graph one unit to the right.
Function is odd because `g(x)=-g(-x)`, so we consider only interval `[0,oo)` and then just reflect result about the origin. Function is not periodic.
There is no y-intercept because `g(0)` is undefined.
There is no x-intercept because there are no points where `g(x)=1/x=0`.
Since `lim_(x->0^+)1/x=+oo` then `x=0` is vertical asymptote.
Since `lim_(x->oo)1/x=0` then `y=0` is horizontal asymptote.
We have that `g'(x)=-1/x^2`. There are no points where derivative equals 0. Point `x=0` is where derivative doesn't exist.
Since `g'(x)=-1/x^2<0` for all `x` then function is decreasing on `(0,+oo)` and there are no extrema according to First Derivative Test.
Second derivative is `g''(x)=2/x^3`. There are no points where `g''(x)=0` and second derivative doesn't exist when `x=0`.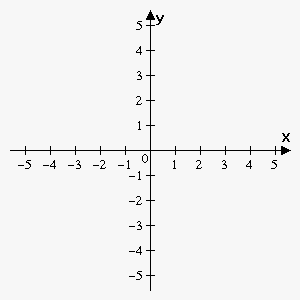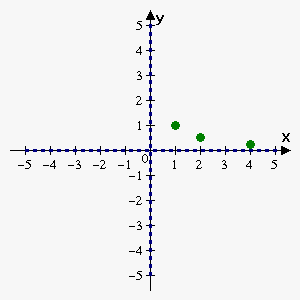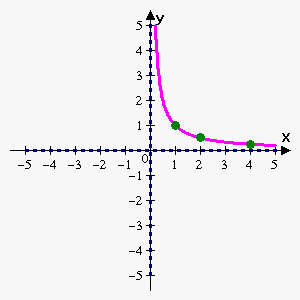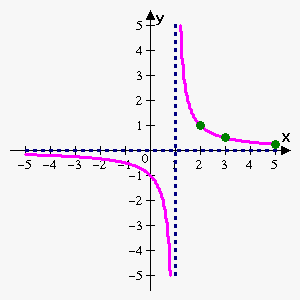
Since second derivative is positive for `x>0` then function is concave upward on `(0,oo)`.
Point `x=0` is not point of inflection because `x=0` is not in the domain of the function.
So, we actually don't have important points, but when `x` approaches 0 from the right function grows without a bound and we can sketch function, taking into account that functions is decreasing and concave upward on `(0,+oo)`. For better graph take a couple of control points: `(1,1),(1,1/2),(4,1/4)`.
Since function is odd, reflect it about origin.
Shift the function 1 unit to the right.
Example 2. Sketch graph of the function `f(x)=(x+2)^2(x-1)^3`.
There is no simpler function that initial function is obtained from.
Function is neither even nor odd and not periodic.
`f(0)=(0+2)^2(0-1)^3=-4`, so y-intercept is -4.
x-intercepts are points where `f(x)=0`: `(x+2)^2(x-1)^3=0` which gives `x=-2` and `x=1`.
Since function is continuous everywhere, `lim_(x->-oo)f(x)=-oo` and `lim_(x->oo)f(x)=oo` then there are no asymptotes.
We have that `f'(x)=2(x+2)(x-1)^3+3(x+2)^2(x-1)^2=(x+2)(x-1)^2(2x-2+3x+6)=`
`=(x+2)(x-1)^2(5x+4)`.
So, derivative equals 0 when `x=-2,x=1,x=-4/5`.
According to method of intervals number line is divided by stationary points on four intervals.
First interval is `(-oo,-2)`: taking any point from this interval, for example `x=-3` we obtain that `f'(-3)=(-3+2)(-3-1)^2(5*(-3)+4)>0`, so `f'(x)>0` on this interval.
Second interval is `(-2,-4/5)`: taking any point from this interval, for example `x=-1` we obtain that `f'(-1)=(-1+2)(-1-1)^2(5*(-1)+4)<0`, so `f'(x)<0` on this interval.
Third interval is `(-4/5,1)`: taking any point from this interval, for example `x=0` we obtain that `f'(0)=(0+2)(0-1)^2(5*(0)+4)>0`, so `f'(x)>0` on this interval.
Fourth interval is `(1,oo)`: taking any point from this interval, for example `x=3` we obtain that `f'(3)=(3+2)(3-1)^2(5*3+4)>0`, so `f'(x)>0` on this interval.
According to First Derivative Test `x=-2` is local maximum, `x=-4/5` is local minimum and `x=1` is not an extremum.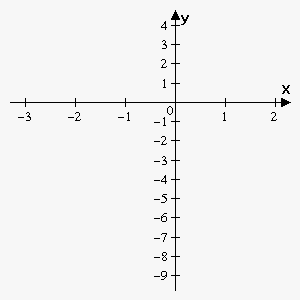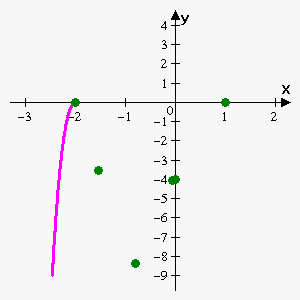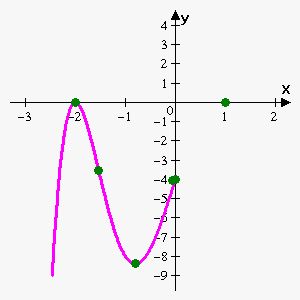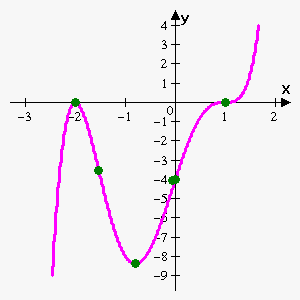
Second derivative is `f''(x)=2(x-1)(10x^2+16x+1)`.
Roots of the equation `10x^2+16x+1=0` are `x=(-8+3sqrt(6))/10~~-0.065` and `x=(-8-3sqrt(6))/10~~-1.535`.
So, points where second derivative equals 0 are `x=1,x=-0.065,x=-1.535`.
Clearly they are all points of inflections because second derivative changes sign at these points.
`f''(x)>0` on `(-1.535,-0.065)uu(1,oo)` and `f''(x)<0` on `(-oo,-1.535)uu(-0.0065,1)`.
So we have following "important" points:
| `x` | -2 | -1.535 | `-4/5` | -0.065 | 0 | 1 |
| `f(x)` | 0 | -3.52241 | -8.3981 | -4.052 | -4 | 0 |
| type | maximum, x-intercept | inflection | minimum | inflection | y-intercept | inflection, x-intercept |
Function is increasing on `(-oo,-2)uu(-4/5,oo)` and decreasing on `(-2,-4/5)`.
Function is concave upward on `(-1.535,-0.065)uu(1,oo)` and concave downward on `(-oo,-1.535)uu(-0.0065,1)`.
Note that points `(-0.065,-4.052)` and `(0,-4)` are very close, so they are almost indistinguishable on graph.
Example 3. Sketch graph of the function `f(x)=(x^2-5x+6)/(x^2+1)`.
There is no simpler function that initial function is obtained from.
Function is neither even nor odd and not periodic.
`f(0)=(0^2-5*0+6)/(0^2+1)=6`, so y-intercept is 6.
x-intercepts are points where `f(x)=0`: `(x^2-5x+6)=(x-2)(x-3)=0` which gives `x=2` and `x=3`.
Since function is continuous everywhere, `lim_(x->oo)(x^2-5x+6)/(x^2+1)=1` then there is only one asymptote: horizontal asymptote `y=1`.
We have that `f'(x)=((x^2-5x+6)'(x^2+1)-(x^2-5x+6)(x^2+1)')/(x^2+1)^2=5(x^2-2x-1)/(x^2+1)^2`.
Roots of the equation `x^2-2x-1=0` are `x=1+sqrt(2)~~2.41` and `x=1-sqrt(2)~~-0.41`.
So, derivative equals 0 when `x=-0.41,x=2.41`.
According to method of intervals number line is divided by stationary points on three intervals.
First interval is `(-oo,-0.41)`: `f'(x)>0` on this interval.
Second interval is `(-0.41,2.41)`:`f'(x)<0` on this interval.
Third interval is `(2.41,oo)`: `f'(x)>0` on this interval.
According to First Derivative Test `x=-0.41` is local maximum, `x=2.41` is local minimum.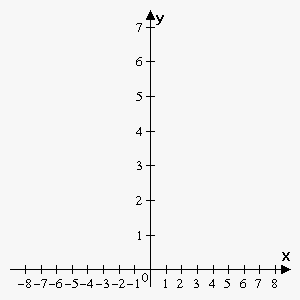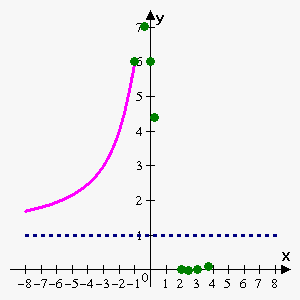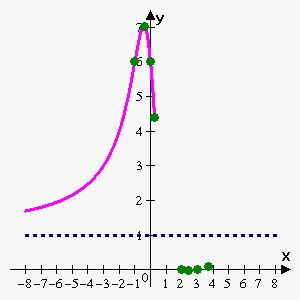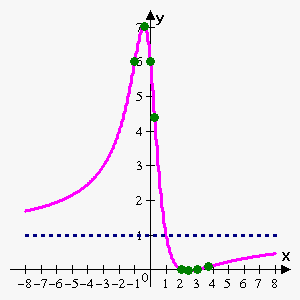
Second derivative is `f''(x)=-10((x+1)(x^2-4x+1))/(x^2+1)^3`.
Roots of the equation `x^2-4x+1=0` are `x=2-sqrt(3)~~0.27` and `x=2+sqrt(3)~~3.73`.
So, points where second derivative equals 0 are `x=-1,x=0.27,x=3.73`.
Clearly they are all points of inflections because second derivative changes sign at these points.
`f''(x)>0` on `(-oo,-1)uu(0.27,3.73)` and `f''(x)<0` on `(-1,0.27)uu(3.73,oo)`.
So we have following "important" points:
| `x` | -1 | -0.41 | 0 | 0.27 | 2 | 2.41 | 3 | 3.73 |
| `f(x)` | 6 | 7.0354 | 6 | 4.402 | 0 | -0.0355 | 0 | 0.0847 |
| type | inflection | maximum | y-intercept | inflection | x-intercept | minimum | x-intercept | inflection |
Function is increasing on `(-oo,-0.41)uu(2.41,oo)` and decreasing on `(-0.41,2.41)`.
Function is concave upward on `(-oo,-1)uu(0.27,3.73)` and concave downward on `(-1,0.27)uu(3.73,oo)`.
Horizontal asymptote is `y=1`.
Example 4. Sketch graph of the function `f(x)=(x-1)^3/(x+1)^2`.
There is no simpler function that initial function is obtained from.
Function is neither even nor odd and not periodic.
`f(0)=(0-1)^3/(0+1)^2=-1`, so y-intercept is -1.
x-intercepts are points where `f(x)=0`: `(x-1)^3=0` which gives `x=1`.
Vertical asymptote is `x=-1` because `lim_(x->-1^+)(x-1)^3/(x+1)^2=-oo`.
There are no horizontal asymptotes because `lim_(x->oo)(x-1)^3/(x+1)^2=oo` and `lim_(x->-oo)(x-1)^3/(x+1)^2=-oo`.
Since `lim_(x->oo)(f(x))/x=lim_(x->oo)(x^3-3x^2+3x-1)/(x^3+2x^2+x)=1` then `m=1`. Now `lim_(x->oo)(f(x)-mx)=(x^3-3x^2+3x-1)/(x^2+2x+1)-x=lim_(x->oo)(-5x^2+2x-1)/(x^2-2x+1)=-5`.
So, there is slant asymptote `y=x-5`.
We have that `f'(x)=(((x-1)^3)'(x+1)^2-(x-1)^3((x+1)^2)')/(x+1)^4=((x-1)^2(x+5))/(x+1)^3`.
Derivative equals 0 when `x=1,x=-5` and doesn't exist when `x=-1`.
Since `(x-1)^2>=0` then these factor doesn't influence sign of derivative.
Thus `f'(x)>0` when `x in (-oo,-5)uu(-1,oo)` and `f'(x)<0` when `x in (-5,-1)`.
According to First Derivative Test `x=-5` is local maximum and `x=1` is not an extremum.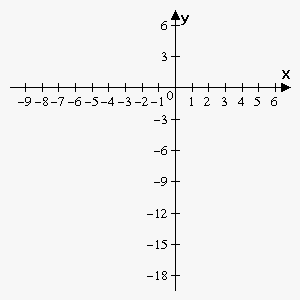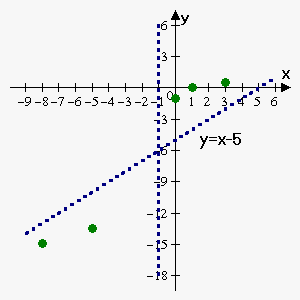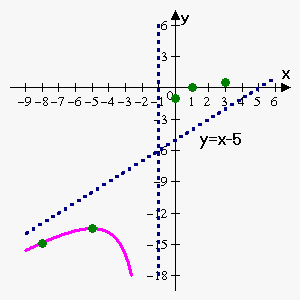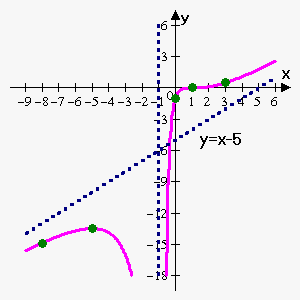
Point `x=-1` is not in the domain of function, so clearly not an extremum.
Second derivative is `f''(x)=24 (x-1)/(x+1)^4`.
So, point where second derivative equals 0 is `x=1`.
Clearly it is inflection point because second derivative changes sign at this point.
`f''(x)>0` when `x>1` and `f''(x)<0` when `x<1`.
Let's add a couple of control points:
`x=3`, `f(3)=0.5`.
`x=-8`, `f(-8)~~-14.88`.
So, we have following points:
| `x` | -8 | -5 | 0 | 1 | 3 |
| `f(x)` | -14.88 | -13.5 | -1 | 0 | 0.5 |
| type | control | maximum | y-intercept | inflection | control |
Function is increasing on `(-oo,-5)uu(-1,oo)` and decreasing on `(-5,-1)`.
Function is concave upward on `(1,oo)` and concave downward on `(-oo,1)`.
Vertical asymptote is `x=-1` and slant asymptote is `y=x-5`.