Transformation of Functions

Example 1. Draw following graphs of functions: $$${y}=\sqrt{{{x}}}$$$, $$${y}=\sqrt{{{x}}}+{5}$$$, $$${y}=\sqrt{{{x}}}-{3}$$$, $$${y}=\sqrt{{{x}-{3}}}$$$, $$${y}=\sqrt{{{x}+{2}}}$$$.

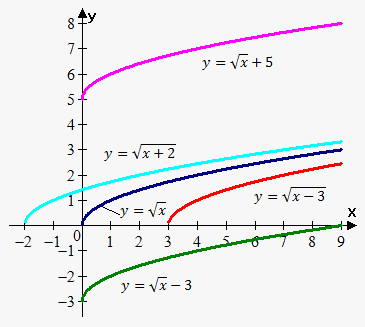We first draw $$${y}=\sqrt{{{x}}}$$$, then we move it 5 units upward to obtain $$${y}=\sqrt{{{x}}}+{5}$$$.

Again we move $$${y}=\sqrt{{{x}}}$$$ 3 units downward to obtain $$${y}=\sqrt{{{x}}}-{3}$$$.

$$${y}=\sqrt{{{x}-{3}}}$$$ is obtained from $$${y}=\sqrt{{{x}}}$$$ by moving it 3 units to the right.

$$${y}=\sqrt{{{x}+{2}}}$$$ is obtained from $$${y}=\sqrt{{{x}}}$$$ by moving it 2 units to the left.

Example 2. Draw following graphs of trigonometric functions: $$${y}={\sin{{\left({x}\right)}}}$$$, $$${y}={2}{\sin{{\left({x}\right)}}}$$$, $$${y}=\frac{{1}}{{4}}{\sin{{\left({x}\right)}}}$$$.

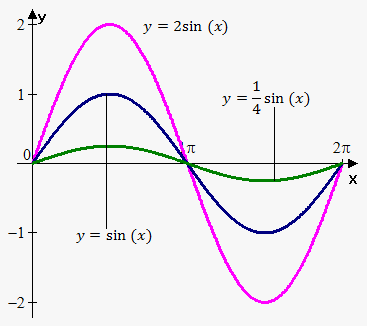We first draw $$${y}={\sin{{\left({x}\right)}}}$$$.

Then stretch it vertically by a factor of 2 to obtain $$${y}={2}{\sin{{\left({x}\right)}}}$$$. Again we compress $$${y}={\sin{{\left({x}\right)}}}$$$ vertically by a factor of 4 to obtain $$${y}=\frac{{1}}{{4}}{\sin{{\left({x}\right)}}}$$$.

Note, that we have drawn graphs only on interval $$${\left[{0},{2}\pi\right]}$$$ because sine is periodic function with period $$${2}\pi$$$.

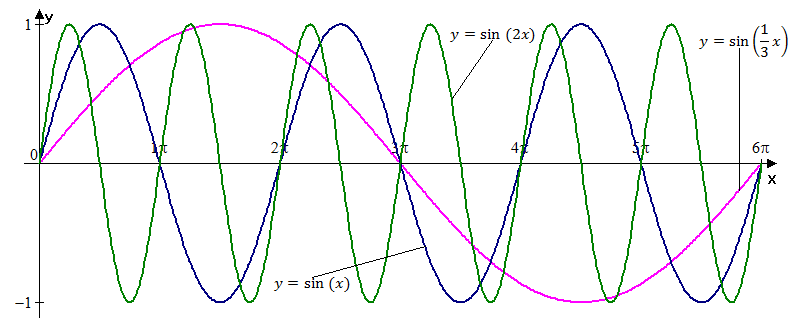
Example 3. Draw following graphs of trigonometric functions: $$${y}={\sin{{\left({x}\right)}}}$$$, $$${y}={\sin{{\left({2}{x}\right)}}}$$$, $$${y}={\sin{{\left(\frac{{1}}{{3}}{x}\right)}}}$$$.

We first draw $$${y}={\sin{{\left({x}\right)}}}$$$.

Then compress it horizontally by a factor of 2 to obtain $$${y}={\sin{{\left({2}{x}\right)}}}$$$.

Again we stretch $$${y}={\sin{{\left({x}\right)}}}$$$ horizontally by a factor of 3 to obtain $$${y}={\sin{{\left(\frac{{1}}{{3}}{x}\right)}}}$$$.

Example 4. Draw following graphs of functions: $$${y}=\sqrt{{{x}}}$$$,

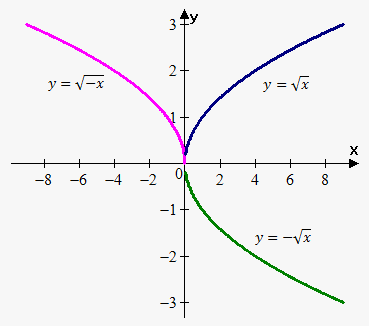$$${y}=-\sqrt{{{x}}}$$$, $$${y}=\sqrt{{-{x}}}$$$.

We first draw $$${y}=\sqrt{{{x}}}$$$ then reflect it about x-axis to obtain $$${y}=-\sqrt{{{x}}}$$$.

Again we reflect $$${y}=\sqrt{{{x}}}$$$ about y-axis to obtain $$${y}=\sqrt{{-{x}}}$$$.

Note that domain of $$${y}=\sqrt{{{x}}}$$$ and $$${y}=-\sqrt{{{x}}}$$$ is $$${x}\ge{0}$$$, while domain of $$${y}=-\sqrt{{{x}}}$$$ is $$${x}\le{0}$$$.

Example 5. How can we obtain graph of the function $$${y}={1}-{2}\sqrt{{{x}}}$$$ from graph of function $$${y}=\sqrt{{{x}}}$$$?

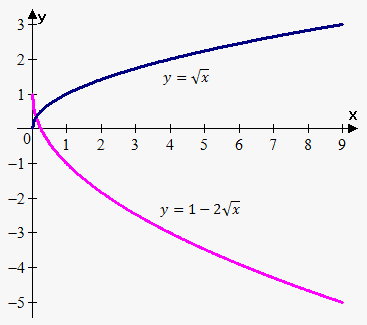We first draw graph of the function $$${y}=\sqrt{{{x}}}$$$.

Then we stretch it vertically to obtain $$${y}={2}\sqrt{{{x}}}$$$.

Then we reflect result about x-axis to obtain $$${y}=-{2}\sqrt{{{x}}}$$$.

Finally, we obtain $$${y}={1}-{2}\sqrt{{{x}}}$$$ by shifting $$${y}=-{2}\sqrt{{{x}}}$$$ 1 unit upward.

Alternatively we could reflect $$${y}=\sqrt{{{x}}}$$$ about x-axis, then stretch result vertically by a factor of 2 and then shift $$${y}=-{2}\sqrt{{{x}}}$$$ 1 unit upward.

Example 6. Draw graph of the function $$${y}={2}{{x}}^{{2}}+{8}{x}+{5}$$$.

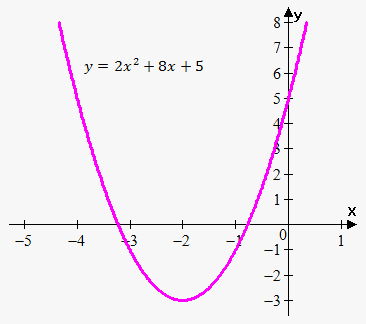First we complete a square: $$${y}={2}{{x}}^{{2}}+{8}{x}+{8}-{3}=$$$

$$$={2}{\left({{x}}^{{2}}+{4}{x}+{4}\right)}-{3}={2}{{\left({x}+{2}\right)}}^{{2}}-{3}$$$.

First of all, let's draw graph of the function $$${y}={{x}}^{{2}}$$$.

Then shift it 2 units to the left.

Then stretch result vertically by a factor of 2.

And finally shift it 3 units downward.

Finalt graph is shown on the picture.