Optimization Problems

Example 1. A man wants to fence off a rectangular field and use a wall as one side. He has 2000 ft of fencing. What are the dimensions of the field that has the largest area?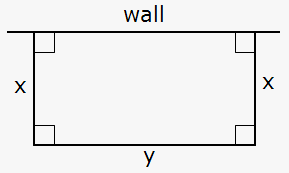

Let's start with the diagram. We wish to maximize the area of the rectangle $$${A}$$$. Let $$${x}$$$ and $$${y}$$$ be the width and the length of the rectangle (in feet). Then, we express $$${A}$$$ terms of $$${x}$$$ and $$${y}$$$: $$${A}={x}{y}$$$.

We want to express $$${A}$$$ as a function of just one variable; so, we eliminate $$${y}$$$ by expressing it in terms of $$${x}$$$. To do this, we use the given information that the total length of the fencing is 2000 ft. Thus, $$${2}{x}+{y}={2000}$$$, or $$${y}={2000}-{2}{x}$$$.

Therefore, $$${A}={x}{y}={x}{\left({2000}-{2}{x}\right)}={2000}{x}-{2}{{x}}^{{2}}$$$.

Note that $$${x}\ge{0}$$$ and $$${x}\le{1000}$$$ (otherwise, $$${A}<{0}$$$). So, the function that we wish to maximize is $$${A}{\left({x}\right)}={2000}{x}-{2}{{x}}^{{2}},$$$ $$${0}\le{x}\le{1000}$$$.

The derivative is $$${A}'{\left({x}\right)}={2000}-{4}{x}$$$.

To find the stationary points, we solve the equation $$${A}'{\left({x}\right)}={2000}-{4}{x}={0}$$$, which gives $$${x}={500}$$$.

The maximum value occurs either at this stationary point or at the endpoints of the interval.

Since $$${A}{\left({0}\right)}={0}$$$, $$${A}{\left({500}\right)}={500000}$$$, and $$${A}{\left({1000}\right)}={0}$$$, the closed interval method gives the maximum value as $$${A}{\left({500}\right)}={500000}$$$.

Thus, the width of the rectangular field should be $$$x=500ft$$$, and the length should be $$${y}={2000}-{2}{x}={1000}{f{{t}}}$$$.

Example 2. Find the point on the parabola $$${y}=\frac{{1}}{{2}}{{x}}^{{2}}$$$ closest to the point $$$(-4,1)$$$.

The distance between the point $$${\left({x},{y}\right)}$$$ and $$${\left(-{4},{1}\right)}$$$ is $$${d}=\sqrt{{{{\left({x}-{\left(-{4}\right)}\right)}}^{{2}}+{{\left({y}-{1}\right)}}^{{2}}}}=\sqrt{{{{\left({x}+{4}\right)}}^{{2}}+{{\left({y}-{1}\right)}}^{{2}}}}$$$.

But since the point $$${\left({x},{y}\right)}$$$ lies on the parabola, we have that $$${y}=\frac{{1}}{{2}}{{x}}^{{2}}$$$ and $$${d}=\sqrt{{{{\left({x}+{4}\right)}}^{{2}}+{{\left(\frac{{1}}{{2}}{{x}}^{{2}}-{1}\right)}}^{{2}}}}$$$.

To make things easier, we minimize $$${{d}}^{{2}}$$$ instead of $$${d}$$$ (if $$${d}$$$ has a minimum, then $$${{d}}^{{2}}$$$ has a minimum at the same point).

So, $$${f{{\left({x}\right)}}}={{d}}^{{2}}={{\left({x}+{4}\right)}}^{{2}}+{{\left(\frac{{1}}{{2}}{{x}}^{{2}}-{1}\right)}}^{{2}}$$$.

Using the chain rule, we obtain $$${f{'}}{\left({x}\right)}={2}{\left({x}+{4}\right)}\cdot{\left({x}+{4}\right)}'+{2}{\left(\frac{{1}}{{2}}{{x}}^{{2}}-{1}\right)}\cdot{\left(\frac{{1}}{{2}}{{x}}^{{2}}-{1}\right)}'={2}{\left({x}+{4}\right)}+{2}{x}{\left(\frac{{1}}{{2}}{{x}}^{{2}}-{1}\right)}=$$$

$$$={{x}}^{{3}}+{8}$$$.

So, $$${f{'}}{\left({x}\right)}={0}$$$ when $$${{x}}^{{3}}+{8}={0}$$$, or $$${x}=-{2}$$$.

Since, $$${f{'}}{\left({x}\right)}<{0}$$$ when $$${x}<-{2}$$$ and $$${f{'}}{\left({x}\right)}>{0}$$$ when $$${x}>-{2}$$$, the first derivative test gives that $$${x}=-{2}$$$ is the absolute minimum.

Now, $$${y}=\frac{{1}}{{2}}{{x}}^{{2}}=\frac{{1}}{{2}}{{\left(-{2}\right)}}^{{2}}={2}$$$.

Therefore, the point that lies on $$${y}=\frac{{1}}{{2}}{{x}}^{{2}}$$$ closest to the point $$${\left(-{4},{1}\right)}$$$ is $$${\left(-{2},{2}\right)}$$$. The corresponding minimum distance is $$${d}=\sqrt{{{{\left(-{2}+{4}\right)}}^{{2}}+{{\left({2}-{1}\right)}}^{{2}}}}=\sqrt{{{5}}}$$$.

Example 3. Suppose that a man is standing at the point $$$A$$$ and wants to reach the point $$$D$$$ as quickly as possible. He could row his boat directly across the river that is 4 km wide to the point $$$B$$$ and then run to $$$D$$$, or he could row directly to $$$D$$$, or he could row to some point between $$$B$$$ and $$$D$$$ and then run to $$$D$$$. If he can row at $$${5}\frac{{{k}{m}}}{{h}}$$$ and run at $$${9}\frac{{{k}{m}}}{{h}}$$$, where should he land to reach $$$D$$$ as soon as possible? Assume that the speed of the water is $$$0$$$. The distance between $$$B$$$ and $$$C$$$ is 8 km.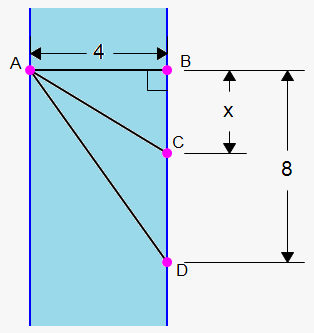

Let $$${x}$$$ be the distance in km from $$$B$$$ to $$$C$$$; then, the running distance $$${\left|{C}{D}\right|}={8}-{\left|{B}{C}\right|}={8}-{x}$$$.

From the right-angled triangle $$$ABC$$$, using the Pythagorean theorem, we have $$${{\left|{A}{C}\right|}}^{{2}}={{\left|{A}{B}\right|}}^{{2}}+{{\left|{B}{C}\right|}}^{{2}}$$$, or $$${{\left|{A}{C}\right|}}^{{2}}={{4}}^{{2}}+{{x}}^{{2}}$$$, which gives $$${\left|{A}{C}\right|}=\sqrt{{{{x}}^{{2}}+{16}}}$$$.

Since time equals distance divided by speed, the time to row the boat is $$$\frac{{\sqrt{{{{x}}^{{2}}+{16}}}}}{{5}}$$$, and the time to run is $$$\frac{{{8}-{x}}}{{9}}$$$.

So, the total time is $$${T}{\left({x}\right)}=\frac{{\sqrt{{{{x}}^{{2}}+{16}}}}}{{5}}+\frac{{{8}-{x}}}{{9}}$$$.

The domain of this function is $$${\left[{0},{8}\right]}$$$. Note that if $$${x}={0}$$$, the man rows to $$$B$$$, and if $$${x}={8}$$$, he rows directly to $$$D$$$.

$$${T}'{\left({x}\right)}=\frac{{1}}{{5}}\cdot\frac{{1}}{{{2}\sqrt{{{{x}}^{{2}}+{16}}}}}\cdot{\left({{x}}^{{2}}+{16}\right)}'-\frac{{1}}{{9}}=\frac{{x}}{{{5}\sqrt{{{{x}}^{{2}}+{16}}}}}-\frac{{1}}{{9}}$$$.

$$${T}'{\left({x}\right)}={0}$$$ when $$$\frac{{x}}{{{5}\sqrt{{{{x}}^{{2}}+{16}}}}}-\frac{{1}}{{9}}={0}$$$, or $$$\frac{{x}}{{{5}\sqrt{{{{x}}^{{2}}+{16}}}}}=\frac{{1}}{{9}}$$$.

This gives $$${9}{x}={5}\sqrt{{{{x}}^{{2}}+{16}}}$$$, or $$${81}{{x}}^{{2}}={25}{\left({{x}}^{{2}}+{16}\right)}$$$.

Thus, $$${{x}}^{{2}}=\frac{{50}}{{7}}$$$, or $$${x}={5}\sqrt{{\frac{{2}}{{7}}}}$$$ (we don't take $$$-{5}\sqrt{{\frac{{2}}{{7}}}}$$$ because this value is not in the domain of $$${T}$$$).

Now, using the closed interval method, we calculate that $$${T}{\left({0}\right)}=\frac{{76}}{{45}}\approx{1.69}$$$, $$${T}{\left({5}\sqrt{{\frac{{2}}{{7}}}}\right)}=\frac{{9}}{{5}}\sqrt{{\frac{{2}}{{7}}}}+\frac{{1}}{{9}}{\left({8}-{5}\sqrt{{\frac{{2}}{{7}}}}\right)}\approx{1.55}$$$, and $$${T}{\left({8}\right)}=\frac{{4}}{\sqrt{{{5}}}}\approx{1.79}$$$.

Since the smallest of these values occurs when $$${x}={5}\sqrt{{\frac{{2}}{{7}}}}$$$, the absolute minimum value of $$${T}$$$ occurs there.

Thus, the man should land the boat at the point $$$C$$$, which is $$${5}\sqrt{{\frac{{2}}{{7}}}}\approx{2.67}$$$ km from the point $$$B$$$.

Example 4. A box with an open top is to be constructed from a square piece of metal with a side of $$${a}$$$ inches by cutting out equal squares of the side $$${x}$$$ at each corner and then folding up the sides. What should be $$${x}$$$ in order to maximize the volume of the box?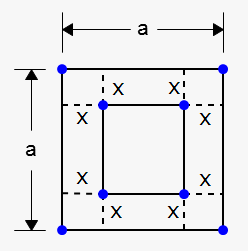

Since we cut out a piece of the length $$${x}$$$, the side of the square box is $$${a}-{2}{x}$$$, the height of the box is $$${x}$$$ (the part that we fold up); so, the volume of the box is $$${V}{\left({x}\right)}={x}{{\left({a}-{2}{x}\right)}}^{{2}}$$$.

Thus, we need to maximize $$${V}{\left({x}\right)}={x}{{\left({a}-{2}{x}\right)}}^{{2}}$$$ on the interval $$${\left[{0},\frac{{a}}{{2}}\right]}$$$ (note that $$${x}$$$ can't be greater than $$$\frac{{a}}{{2}}$$$).

We have that $$${V}_{{x}}'={{\left({a}-{2}{x}\right)}}^{{2}}+{2}{x}{\left({a}-{2}{x}\right)}\cdot{\left(-{2}\right)}={\left({a}-{2}{x}\right)}{\left({a}-{2}{x}-{4}{x}\right)}=$$$

$$$={\left({a}-{2}{x}\right)}{\left({a}-{6}{x}\right)}$$$.

So, $$${V}'{\left({x}\right)}={0}$$$ when $$${x}=\frac{{a}}{{2}}$$$ (endpoint) and $$${x}=\frac{{a}}{{6}}$$$.

Now, calculate the values of the function at the endpoints and the stationary points:

$$${V}{\left({0}\right)}={0}$$$, $$${V}{\left(\frac{{a}}{{2}}\right)}={0}$$$, $$${V}{\left(\frac{{a}}{{6}}\right)}=\frac{{a}}{{6}}{{\left({a}-{2}\frac{{a}}{{6}}\right)}}^{{2}}=\frac{{{2}{{a}}^{{3}}}}{{27}}$$$.

The greatest value is $$$\frac{{{2}{{a}}^{{3}}}}{{27}}$$$; so, the maximum occurs when $$${x}=\frac{{a}}{{6}}$$$.

Example 5. Find the area of the largest rectangle that can be inscribed in a semicircle of the radius $$${r}$$$.

Solution 1. Let's take the semicircle to be the upper half of a circle $$${{x}}^{{2}}+{{y}}^{{2}}={{r}}^{{2}}$$$ with the center at the origin. Then, the word 'inscribed' means that the rectangle has two vertices on the semicircle and two vertices on the x-axis.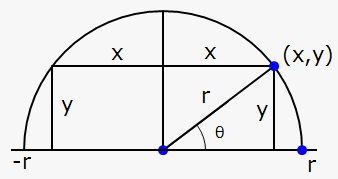

Let $$${\left({x},{y}\right)}$$$ be the vertex that lies in the first quadrant. Then, the rectangle has the sides of the lengths $$${2}{x}$$$ and $$${y}$$$; so, its area is $$${A}={2}{x}{y}$$$.

To eliminate $$${y}$$$, we use the fact that the point $$${\left({x},{y}\right)}$$$ lies on the circle; so, $$${{x}}^{{2}}+{{y}}^{{2}}={{r}}^{{2}}$$$, or $$${y}=\sqrt{{{{r}}^{{2}}-{{x}}^{{2}}}}$$$.

Therefore, $$${A}={2}{x}\sqrt{{{{r}}^{{2}}-{{x}}^{{2}}}}$$$ for $$${0}\le{x}\le{r}$$$.

Using the product rule and the chain rule, we obtain that $$${A}'{\left({x}\right)}={\left({2}{x}\right)}'\sqrt{{{{r}}^{{2}}-{{x}}^{{2}}}}+{2}{x}{\left(\sqrt{{{{r}}^{{2}}-{{x}}^{{2}}}}\right)}'={2}\sqrt{{{{r}}^{{2}}-{{x}}^{{2}}}}+\frac{{x}}{{\sqrt{{{{r}}^{{2}}-{{x}}^{{2}}}}}}\cdot{\left({{r}}^{{2}}-{{x}}^{{2}}\right)}'=$$$

$$$={2}\sqrt{{{{r}}^{{2}}-{{x}}^{{2}}}}-\frac{{{2}{{x}}^{{2}}}}{{\sqrt{{{{r}}^{{2}}-{{x}}^{{2}}}}}}={2}\frac{{{{r}}^{{2}}-{2}{{x}}^{{2}}}}{{\sqrt{{{{r}}^{{2}}-{{x}}^{{2}}}}}}$$$.

We have to find the maximum of $$${A}{\left({x}\right)}$$$ on the closed interval $$${\left[{0},{r}\right]}$$$.

So, $$${A}'{\left({x}\right)}={0}$$$ when $$${{r}}^{{2}}-{2}{{x}}^{{2}}={0}$$$, or $$${x}=\frac{{r}}{{\sqrt{{{2}}}}}$$$ (we don't take $$$-\frac{{r}}{{\sqrt{{{2}}}}}$$$ because $$${x}$$$ should be non-negative).

Now, check the endpoints: $$${A}{\left({0}\right)}={0}$$$, $$${A}{\left({r}\right)}={0}$$$.

Since $$${A}{\left(\frac{{r}}{\sqrt{{{2}}}}\right)}={2}{\left(\frac{{r}}{\sqrt{{{2}}}}\right)}\sqrt{{{{r}}^{{2}}-{{\left(\frac{{r}}{\sqrt{{{2}}}}\right)}}^{{2}}}}={{r}}^{{2}}>{0}$$$, the maximum occurs when $$${x}=\frac{{r}}{{\sqrt{{{2}}}}}$$$.

The largest possible area is $$${{r}}^{{2}}$$$.

Solution 2. There is another solution. Connect the center of the circle with the point $$${\left({x},{y}\right)}$$$. If $$$\theta$$$ is the angle between the drawn line and the positive direction of the x-axis, then $$${x}={r}{\cos{{\left(\theta\right)}}}$$$ and $$${y}={r}{\sin{{\left(\theta\right)}}}$$$.

The area can be rewritten as $$${A}={2}{x}{y}={2}{r}{\cos{{\left(\theta\right)}}}{r}{\sin{{\left(\theta\right)}}}={{r}}^{{2}}{\sin{{\left({2}\theta\right)}}}$$$.

Since $$${\sin{{\left({2}\theta\right)}}}\le{1}$$$, the maximum occurs when $$${\sin{{\left({2}\theta\right)}}}={1}$$$, or $$${2}\theta=\frac{\pi}{{2}}$$$, which gives $$$\theta=\frac{\pi}{{4}}$$$.

In this case, $$${A}={{r}}^{{2}}$$$, $$${x}={r}{\cos{{\left(\frac{\pi}{{4}}\right)}}}=\frac{{r}}{{\sqrt{{{2}}}}}$$$, and $$${y}={r}{\sin{{\left(\frac{\pi}{{4}}\right)}}}=\frac{{r}}{{\sqrt{{{2}}}}}$$$, which are the same answers as in Solution 1.

Note that in Solution 2 we didn't use the derivatives and calculus at all.