Closed Interval Method

In fact when we used derivative to find extrema, this extrema mainly were local.

Now we turn our attention to finding global extrema on closed interval ${\left[{a},{b}\right]}$ .

Extreme Value Theorem. If ${f{}}$ is continuous on a closed interval ${\left[{a},{b}\right]}$ , then ${f{}}$ attains a global maximum value ${f{{\left({c}\right)}}}$ and a global minimum value ${f{{\left({d}\right)}}}$ at some numbers ${c}$ and ${d}$ from interval ${\left[{a},{b}\right]}$ .

Extreme values can be taken either at endpoints of interval or inside it. On the figure below one case is when both extrema are taken at endpoints and another case when both extrema are taken inside interval. Of course there can be cases when one extremum is at endpoint and another is inside interval.

Note that extreme value can be taken more than once.

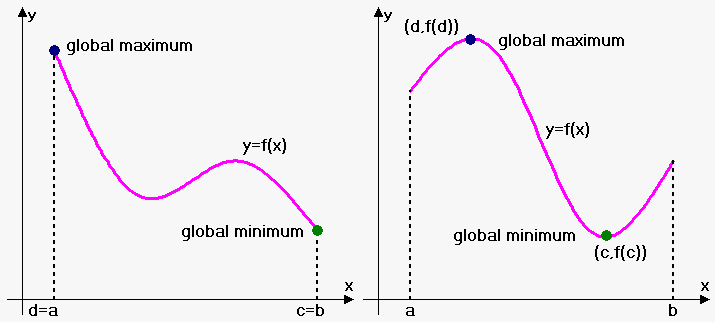extreme value theorem This theorem doesn't hold when either interval is not closed or function is not continuous.

For example, consider function ${f{{\left({x}\right)}}}=\frac{{1}}{{{x}-{1}}}$ on interval ${\left[{0},{2}\right]}$ . It is discontinuous at ${x}={1}$ . Since $\lim_{{{x}\to{{1}}^{{}}}}\frac{{1}}{{{x}-{1}}}=\infty$ and $\lim_{{{x}\to{{1}}^{{-}}}}\frac{{1}}{{{x}-{1}}}=-\infty$ then function doesn't attain neither global maximum, nor global minimum.

Now consider function ${g{{\left({x}\right)}}}=\frac{{1}}{{{x}-{1}}}$ on interval ${\left({1},{2}\right)}$ (note that interval is not closed). It is continuous on this interval and decreasing. Since $\lim_{{{x}\to{{1}}^{+}}}\frac{{1}}{{{x}-{1}}}=\infty$ then function grows without a bound and so there is no global maximum. Since $\lim_{{{x}\to{{2}}^{{-}}}}\frac{{1}}{{{x}-{1}}}={1}$ then function approaches minimum value ${1}$ , but never attains it! So, there are no global minimum as well.

Although Extreme Value Theorem states that for continuous function on closed interval there are global maxima and minima but it doesn't tell us how to find them.

Luckily, we already know how to find local extrema and on closed interval global extrema occurs either at stationary points or on endpoints of interval.

Closed Interval Method. To find the global maximum and minimum values of a continuous function ${f{}}$ on a closed interval ${\left[{a},{b}\right]}$ we need to do following three steps:

Find the values of ${f{}}$ at the stationary points of ${f{}}$ in ${\left({a},{b}\right)}$ .
Find the values of ${f{}}$ at the endpoints of the interval.
The largest of the values from Steps 1 and 2 is the global maximum value; the smallest of these values is the global minimum value.

Example. Find global extrema of ${f{{\left({x}\right)}}}={{x}}^{{3}}-{3}{{x}}^{{2}}+{1}$ on interval ${\left[-{2},{2.5}\right]}$ .

We have that ${f{'}}{\left({x}\right)}={3}{{x}}^{{2}}-{6}{x}$ . ${f{'}}{\left({x}\right)}={0}$ when ${x}={0}$ and ${x}={2}$ .

There are no ${x}$ such that ${f{'}}{\left({x}\right)}$ doesn't exist.

Therefore stationary points are ${x}={0}$ and ${x}={2}$ .

Now find values of function at stationary points:

${f{{\left({0}\right)}}}={{0}}^{{3}}-{3}\cdot{{0}}^{{2}}+{1}={1}$ and ${f{{\left({2}\right)}}}={{2}}^{{3}}-{3}\cdot{{2}}^{{2}}+{1}=-{3}$ .

Calculate values of ${f{}}$ at the endpoints:

${f{{\left(-{2}\right)}}}={{\left(-{2}\right)}}^{{3}}-{3}\cdot{{\left(-{2}\right)}}^{{2}}+{1}=-{19}$ and ${f{{\left({2.5}\right)}}}={{2.5}}^{{3}}-{3}\cdot{\left({{2.5}}^{{2}}\right)}+{1}=-{2.125}$ .

So, the largest value is ${f{{\left({0}\right)}}}={1}$ - this is global maximum; and the smallest value is ${f{{\left(-{2}\right)}}}=-{19}$ - this is global minimum.