Asymptotes
Definition. The line $$$x=a$$$ is called vertical asymptote of the curve $$$y=f{{\left({x}\right)}}$$$ if at least one of the following statements is true:
- $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\infty$$$
- $$$\lim_{{{x}\to{{a}}^{+}}}{f{{\left({x}\right)}}}=\infty$$$
- $$$\lim_{{{x}\to{{a}}^{{-}}}}{f{{\left({x}\right)}}}=\infty$$$
- $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=-\infty$$$
- $$$\lim_{{{x}\to{{a}}^{+}}}{f{{\left({x}\right)}}}=-\infty$$$
- $$$\lim_{{{x}\to{{a}}^{{-}}}}{f{{\left({x}\right)}}}=-\infty$$$
For example y-axis $$$\left({x}={0}\right)$$$ is a vertical asymptote of the curve $$${y}=\frac{{1}}{{{x}}^{{2}}}$$$ because $$$\lim_{{{x}\to{0}}}\frac{{1}}{{{x}}^{{2}}}=\infty$$$.
Geometrically vertical asymptote is vertical line to which approaches graph of the function but never intersects it. As function approaches $$${a}$$$ values of function become so large, that we can't draw them.
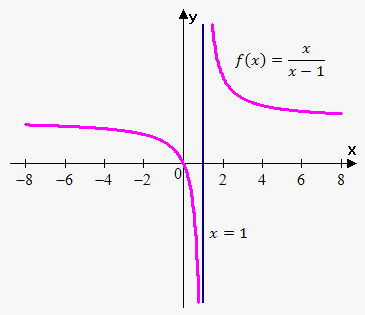 Example 1. Find vertical asymptotes of $$${f{{\left({x}\right)}}}=\frac{{x}}{{{x}-{1}}}$$$.
Example 1. Find vertical asymptotes of $$${f{{\left({x}\right)}}}=\frac{{x}}{{{x}-{1}}}$$$.
In Limits Involving Infinity note we saw that if $$$\lim_{{{x}\to{{a}}^{+}}}{f{{\left({x}\right)}}}={L}\ne{0}$$$ and $$$\lim_{{{x}\to{a}+}}{g{{\left({x}\right)}}}={0}$$$ then $$$\lim_{{{x}\to{{a}}^{+}}}{\left(\frac{{f{{\left({x}\right)}}}}{{g{{\left({x}\right)}}}}\right)}=\infty$$$ (Law 8 for one-sided limits).
So, to find points where function approach infinity, we need to find points where denominator equals 0, and make sure that numerator doesn't equal 0 at this point.
The only point where denominator equals 0 is point 1, and numerator doesn't equal 0 at this point.
Let's find out one-sided limits at this point. When $$${x}$$$ approaches 1 from the right then $$${x}-{3}$$$ becomes very small positive value and $$${x}$$$ approaches 1. Thus, $$$\lim_{{{x}\to{{1}}^{+}}}\frac{{{x}}}{{{x}-{1}}}=\infty$$$ When $$${x}$$$ approaches 1 from the left then $$${x}-{1}$$$ becomes very small negative value and $$${x}$$$ approaches 1. Thus, $$$\lim_{{{x}\to{{1}}^{{-}}}}\frac{{{x}}}{{{x}-{1}}}=-\infty$$$. So, we showed that both one-sided limits are infinite. In fact it was sufficiently to show that at least one of the limits is infinite.
Thus, $$${x}={1}$$$ is vertical asympote.
In fact function can have more than vertical asymptote.
Example 2. Find vertical asymptotes of $$${y}={\tan{{\left({x}\right)}}}$$$.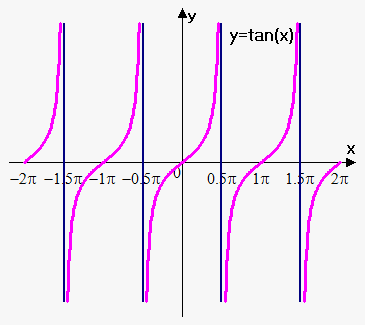
Recall that by definition $$${\tan{{\left({x}\right)}}}=\frac{{{\sin{{\left({x}\right)}}}}}{{{\cos{{\left({x}\right)}}}}}$$$.
This means that there will be vertical asymptotes at points where $$${\cos{{\left({x}\right)}}}={0}$$$, i.e. points of the form $$${x}=\frac{\pi}{{2}}+\pi{k},{k}\in\mathbb{Z}$$$.
Therefore, $$${\tan{{\left({x}\right)}}}$$$ has infinitely many asymptotes.
Example 3. Find vertical asymptotes of $$${f{{\left({x}\right)}}}=\frac{{{{x}}^{{2}}-{x}}}{{{{x}}^{{2}}+{x}-{2}}}$$$.
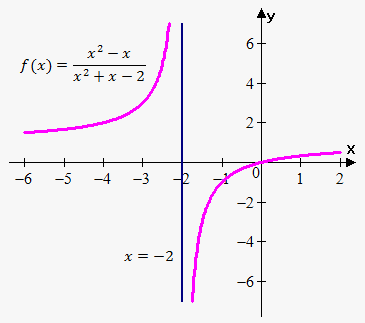 Since $$${{x}}^{{2}}+{x}-{2}={\left({x}+{2}\right)}{\left({x}-{1}\right)}$$$ then denominator equals 0 when $$${x}=-{2}$$$ and $$${x}={1}$$$.
Since $$${{x}}^{{2}}+{x}-{2}={\left({x}+{2}\right)}{\left({x}-{1}\right)}$$$ then denominator equals 0 when $$${x}=-{2}$$$ and $$${x}={1}$$$.
However, at point $$${x}={1}$$$ numerator also equals 0. We need to additionally check this point.So, $$$\lim_{{{x}\to{1}}}\frac{{{{x}}^{{2}}-{x}}}{{{{x}}^{{2}}+{x}-{2}}}=\lim_{{{x}\to{1}}}\frac{{{x}{\left({x}-{1}\right)}}}{{{\left({x}+{2}\right)}{\left({x}-{1}\right)}}}=$$$
$$$=\lim_{{{x}\to{1}}}\frac{{x}}{{{x}+{2}}}=\frac{{1}}{{{1}+{2}}}=\frac{{1}}{{3}}$$$.
Thus, there is only one vertical asymptote $$${x}=-{2}$$$. This example showed, that you should be very cautious: you should check whether numerator equals 0 at points where denominator equals 0.
Definition. Line $$${y}={L}$$$ is called horizontal asymptote of the function $$${f{{\left({x}\right)}}}$$$ if either $$$\lim_{{{x}\to\infty}}{f{{\left({x}\right)}}}={L}$$$ or $$$\lim_{{{x}\to-\infty}}{f{{\left({x}\right)}}}={L}$$$.
Example 4. Find horizontal asymptotes of $$${y}={1}+\frac{{1}}{{x}}$$$.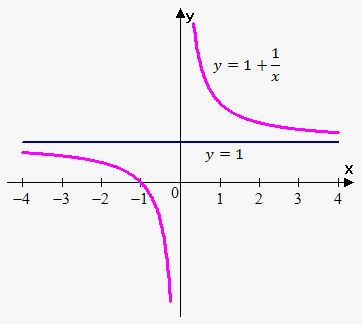
Since $$$\lim_{{{x}\to\infty}}{\left({1}+\frac{{1}}{{x}}\right)}={1}$$$ then line $$${y}={1}$$$ is horizontal asymptote.
In fact also $$$\lim_{{{x}\to-\infty}}{\left({1}+\frac{{1}}{{x}}\right)}={1}$$$, but it suffices one limit to state that $$${y}={1}$$$ is horizontal asymptote.
In general function can have more than one horizontal asymptote.
Example 5. Find horizontal asymptotes of $$${y}={\operatorname{arctan}{{\left({x}\right)}}}$$$.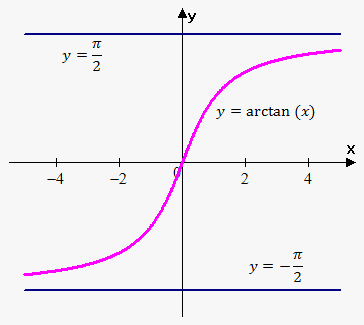
Since $$$\lim_{{{x}\to\infty}}{\operatorname{arctan}{{\left({x}\right)}}}=\frac{\pi}{{2}}$$$ and $$$\lim_{{{x}\to-\infty}}{\operatorname{arctan}{{\left({x}\right)}}}=-\frac{\pi}{{2}}$$$ then there are two vertical asymptotes: $$${y}=\frac{\pi}{{2}}$$$ and $$${y}=-\frac{\pi}{{2}}$$$.
Definition. Line $$${y}={m}{x}+{b}$$$ is called slant (oblique) asymptote of function $$${y}={f{{\left({x}\right)}}}$$$ if either $$$\lim_{{{x}\to\infty}}{\left({f{{\left({x}\right)}}}-{\left({m}{x}+{b}\right)}\right)}={0}$$$ or $$$\lim_{{{x}\to-\infty}}{\left({f{{\left({x}\right)}}}-{\left({m}{x}+{b}\right)}\right)}={0}$$$.
We calculate $$${m}$$$ as follows: $$${m}=\lim_{{{x}\to\infty}}\frac{{{f{{\left({x}\right)}}}}}{{x}}{\left({m}=\lim_{{{x}\to-\infty}}\frac{{{f{{\left({x}\right)}}}}}{{x}}\right)}$$$.
If this limit is not finite or doesn't exist then there is no oblique asymptote.
$$${b}$$$ is calculated as follows: $$${b}=\lim_{{{x}\to\infty}}{\left({f{{\left({x}\right)}}}-{m}{x}\right)}{\left({b}=\lim_{{{x}\to-\infty}}{\left({f{{\left({x}\right)}}}-{m}{x}\right)}\right)}$$$.
Example 6. Find all asymptotes of $$${y}={x}+\frac{{1}}{{x}}$$$.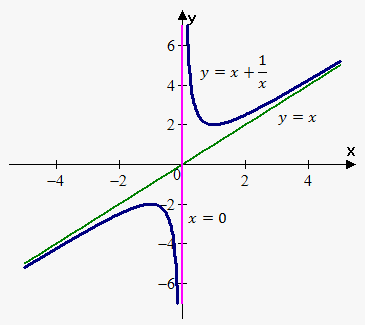
There are no horizontal asymptotes because $$$\lim_{{{x}\to\infty}}{\left({x}+\frac{{1}}{{x}}\right)}=\infty$$$ and $$$\lim_{{{x}\to-\infty}}{\left({x}+\frac{{1}}{{x}}\right)}=-\infty$$$.
There is vertical asymptote $$${x}={0}$$$ because $$$\lim_{{{x}\to{{0}}^{+}}}{\left({x}+\frac{{1}}{{x}}\right)}=\infty$$$.
This function also has oblique asymptote. Indeed, $$${m}=\lim_{{{x}\to\infty}}\frac{{{x}+\frac{{1}}{{x}}}}{{x}}=\lim_{{{x}\to\infty}}{\left({1}+\frac{{1}}{{{x}}^{{2}}}\right)}={1}$$$.
So, $$${m}={1}$$$. Now, $$${b}=\lim_{{{x}\to\infty}}{\left({x}+\frac{{1}}{{x}}-{1}\cdot{x}\right)}=\lim_{{{x}\to\infty}}\frac{{1}}{{x}}={0}$$$. So, $$${b}={0}$$$.
Therefore, slant asymptote is $$${y}={x}$$$. On the figure to the right blue line is vertical asymptote $$${x}={0}$$$, green line is slant asymptote $$${y}={x}$$$.
Note, that we will obtain same slant asymptote when $$${x}\to-\infty$$$.
In general, it is a good practice to treat cases $$${x}\to\infty$$$ and $$${x}\to-\infty$$$ separately.
