Indeterminate Forms for Functions
In the note Limits Involving Infinity we saw that it is pretty easy to evaluate $$$\lim_{{{x}\to{0}}}\frac{{{x}+{1}}}{{x}}$$$ because since $$$\lim_{{{x}\to{0}}}{\left({x}+{1}\right)}={1}$$$ and $$$\lim_{{{x}\to{0}}}{x}={0}$$$ then division of 1 by very small number will give very large number, and so $$$\lim_{{{x}\to{0}}}\frac{{{x}+{1}}}{{x}}=\infty$$$.
But there are some cases when it is not so easy to calculate limit. In fact we can't state limit in general without knowing functions.
There are 4 cases.
Case 1. Suppose that $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={0}$$$ and $$$\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}={0}$$$. We need to find $$$\lim_{{{x}\to{a}}}\frac{{f{{\left({x}\right)}}}}{{g{{\left({x}\right)}}}}$$$.
It is not very clear what is the limit of the ratio and does it exist at all. Very small number divided by the very small number can give anything.
Let $$${f{{\left({x}\right)}}}=\frac{{1}}{{x}}$$$ and $$${g{{\left({x}\right)}}}=\frac{{1}}{{{x}}^{{2}}}$$$. Clearly $$$\lim_{{{x}\to\infty}}\frac{{1}}{{x}}={0}$$$ and $$$\lim_{{{x}\to\infty}}\frac{{1}}{{{x}}^{{2}}}={0}$$$. Then $$$\lim_{{{x}\to\infty}}\frac{{{f{{\left({x}\right)}}}}}{{{g{{\left({x}\right)}}}}}=\lim_{{{x}\to\infty}}\frac{{\frac{{1}}{{x}}}}{{\frac{{1}}{{{x}}^{{2}}}}}=\lim_{{{x}\to\infty}}{x}=\infty$$$.
Let $$${f{{\left({x}\right)}}}=\frac{{1}}{{{x}}^{{2}}}$$$ and $$${g{{\left({x}\right)}}}=\frac{{1}}{{x}}$$$. Clearly $$$\lim_{{{x}\to\infty}}\frac{{1}}{{{x}}^{{2}}}={0}$$$ and $$$\lim_{{{x}\to\infty}}\frac{{1}}{{x}}={0}$$$. Then $$$\lim_{{{x}\to\infty}}\frac{{{f{{\left({x}\right)}}}}}{{{g{{\left({x}\right)}}}}}=\lim_{{{x}\to\infty}}\frac{{\frac{{1}}{{{x}}^{{2}}}}}{{\frac{{1}}{{x}}}}=\lim_{{{x}\to\infty}}\frac{{1}}{{x}}={0}$$$.
Let $$${f{{\left({x}\right)}}}=\frac{{3}}{{x}}$$$ and $$${g{{\left({x}\right)}}}=\frac{{1}}{{x}}$$$. Clearly $$$\lim_{{{x}\to\infty}}\frac{{3}}{{x}}={0}$$$ and $$$\lim_{{{x}\to\infty}}\frac{{1}}{{x}}={0}$$$. Then $$$\lim_{{{x}\to\infty}}\frac{{{f{{\left({x}\right)}}}}}{{{g{{\left({x}\right)}}}}}=\lim_{{{x}\to\infty}}\frac{{\frac{{3}}{{x}}}}{{\frac{{1}}{{x}}}}=\lim_{{{x}\to\infty}}{3}={3}$$$.
Let $$${f{{\left({x}\right)}}}={x}$$$ and $$${g{{\left({x}\right)}}}={{x}}^{{2}}$$$. Clearly $$$\lim_{{{x}\to{0}}}{x}={0}$$$ and $$$\lim_{{{x}\to{0}}}{{x}}^{{2}}={0}$$$. Then $$$\lim_{{{x}\to\infty}}\frac{{{f{{\left({x}\right)}}}}}{{{g{{\left({x}\right)}}}}}=\lim_{{{x}\to\infty}}\frac{{x}}{{{{x}}^{{2}}}}=\lim_{{{x}\to{0}}}\frac{{1}}{{x}}$$$ doesn't exist because $$$\lim_{{{x}\to{{0}}^{+}}}\frac{{1}}{{x}}=\infty$$$ and $$$\lim_{{{x}\to{{0}}^{{-}}}}\frac{{1}}{{x}}=-\infty$$$ so one-sided limits are not equal.
Therefore, in general case we can't find limit of ratio without knowing functions.
To characterize this special case we say that when $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={0}$$$ and $$$\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}={0}$$$, expression $$$\lim_{{{x}\to{a}}}\frac{{{f{{\left({x}\right)}}}}}{{{g{{\left({x}\right)}}}}}$$$ is indeterminate form of type $$$\frac{0}{0}$$$.
Case 2. Suppose that $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\pm\infty$$$ and $$$\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}=\pm\infty$$$. We need to find $$$\lim_{{{x}\to{a}}}\frac{{{f{{\left({x}\right)}}}}}{{{g{{\left({x}\right)}}}}}$$$.
Again it is not very clear what is the limit of the ratio and does it exist at all. Very large number divided by the very large number can give anything.
Let $$${f{{\left({x}\right)}}}=\frac{{1}}{{{x}}^{{2}}}$$$ and $$${g{{\left({x}\right)}}}=\frac{{1}}{{{x}}^{{4}}}$$$. Clearly $$$\lim_{{{x}\to{0}}}\frac{{1}}{{{x}}^{{2}}}=\infty$$$ and $$$\lim_{{{x}\to{0}}}\frac{{1}}{{{x}}^{{4}}}=\infty$$$. Then $$$\lim_{{{x}\to{0}}}\frac{{{f{{\left({x}\right)}}}}}{{{g{{\left({x}\right)}}}}}=\lim_{{{x}\to{0}}}\frac{{\frac{{1}}{{{x}}^{{2}}}}}{{\frac{{1}}{{{x}}^{{4}}}}}=\lim_{{{x}\to{0}}}{{x}}^{{2}}={0}$$$.
Let $$${f{{\left({x}\right)}}}=\frac{{1}}{{{x}}^{{4}}}$$$ and $$${g{{\left({x}\right)}}}=\frac{{1}}{{{x}}^{{2}}}$$$. Clearly $$$\lim_{{{x}\to{0}}}\frac{{1}}{{{x}}^{{4}}}=\infty$$$ and $$$\lim_{{{x}\to{0}}}\frac{{1}}{{{x}}^{{2}}}=\infty$$$. Then $$$\lim_{{{x}\to{0}}}\frac{{{f{{\left({x}\right)}}}}}{{{g{{\left({x}\right)}}}}}=\lim_{{{x}\to{0}}}\frac{{\frac{{1}}{{{x}}^{{4}}}}}{{\frac{{1}}{{{x}}^{{2}}}}}=\lim_{{{x}\to{0}}}\frac{{1}}{{{x}}^{{2}}}=\infty$$$.
Let $$${f{{\left({x}\right)}}}=\frac{{2}}{{{x}}^{{2}}}$$$ and $$${g{{\left({x}\right)}}}=\frac{{1}}{{{x}}^{{2}}}$$$. Clearly $$$\lim_{{{x}\to{0}}}\frac{{2}}{{{x}}^{{2}}}=\infty$$$ and $$$\lim_{{{x}\to{0}}}\frac{{1}}{{{x}}^{{2}}}=\infty$$$. Then $$$\lim_{{{x}\to{0}}}\frac{{{f{{\left({x}\right)}}}}}{{{g{{\left({x}\right)}}}}}=\lim_{{{x}\to{0}}}\frac{{\frac{{2}}{{{x}}^{{2}}}}}{{\frac{{1}}{{{x}}^{{2}}}}}=\lim_{{{x}\to{0}}}{2}={2}$$$.
Again, in general case we can't find limit of ratio without knowing functions.
To characterize this special case we say that when $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\pm\infty$$$ and $$$\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}=\pm\infty$$$, expression $$$\lim_{{{x}\to{a}}}\frac{{{f{{\left({x}\right)}}}}}{{{g{{\left({x}\right)}}}}}$$$ is indeterminate form of type $$$\frac{\infty}{\infty}$$$.
Actually we can trasnform this indeterminate form in indeterminate form of type $$$\frac{{0}}{{0}}$$$.
Indeed, since $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\infty$$$ and $$$\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}=\infty$$$ then $$$\lim_{{{x}\to{a}}}\frac{{1}}{{{f{{\left({x}\right)}}}}}={0}$$$ and $$$\lim_{{{x}\to{a}}}\frac{{1}}{{{g{{\left({x}\right)}}}}}={0}$$$.
So, $$$\lim_{{{x}\to{a}}}\frac{{{f{{\left({x}\right)}}}}}{{{g{{\left({x}\right)}}}}}=\lim_{{{x}\to{a}}}\frac{{\frac{{1}}{{{g{{\left({x}\right)}}}}}}}{{\frac{{1}}{{{f{{\left({x}\right)}}}}}}}$$$.
Case 3. Suppose that $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={0}$$$ and $$$\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}=\pm\infty$$$. We need to find $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}{g{{\left({x}\right)}}}$$$.
Again it is not very clear what is the product of very small number and very large number.
This case can be transformed either into case 1 or into case 2.
Indeed, since $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={0}$$$ then $$$\lim_{{{x}\to{a}}}\frac{{1}}{{{f{{\left({x}\right)}}}}}=\infty$$$. Therefore, we can write product as indeterminate form of type $$$\frac{{\infty}}{{\infty}}$$$: $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}{g{{\left({x}\right)}}}=\lim_{{{x}\to{a}}}\frac{{{g{{\left({x}\right)}}}}}{{\frac{{1}}{{{f{{\left({x}\right)}}}}}}}$$$.
Similarly, since $$$\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}={0}$$$ then $$$\lim_{{{x}\to{a}}}\frac{{1}}{{{g{{\left({x}\right)}}}}}={0}$$$. Therefore, we can write product as indeterminate form of type $$$\frac{{{0}}}{{{0}}}$$$: $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}{g{{\left({x}\right)}}}=\lim_{{{x}\to{a}}}\frac{{{f{{\left({x}\right)}}}}}{{\frac{{1}}{{{g{{\left({x}\right)}}}}}}}$$$.
So, we have third indeterminate form: indeterminate form of type $$$0\cdot\infty$$$.
Case 4. Finally, suppose that $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\infty$$$ and $$$\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}=\infty$$$. We need to find $$$\lim_{{{x}\to{a}}}{\left({f{{\left({x}\right)}}}-{g{{\left({x}\right)}}}\right)}$$$.
Again it is not clear what will be difference of very large numbers.
Let $$${f{{\left({x}\right)}}}={x}$$$ and $$${g{{\left({x}\right)}}}={2}{x}$$$. Clearly $$$\lim_{{{x}\to\infty}}{x}=\infty$$$ and $$$\lim_{{{x}\to\infty}}{2}{x}=\infty$$$. Then $$$\lim_{{{x}\to\infty}}{\left({f{{\left({x}\right)}}}-{g{{\left({x}\right)}}}\right)}=\lim_{{{x}\to\infty}}{\left({x}-{2}{x}\right)}=\lim_{{{x}\to\infty}}-{x}=-\infty$$$.
Let $$${f{{\left({x}\right)}}}={3}{x}$$$ and $$${g{{\left({x}\right)}}}={x}$$$. Clearly $$$\lim_{{{x}\to\infty}}{3}{x}=\infty$$$ and $$$\lim_{{{x}\to\infty}}{x}=\infty$$$. Then $$$\lim_{{{x}\to\infty}}{\left({f{{\left({x}\right)}}}-{g{{\left({x}\right)}}}\right)}=\lim_{{{x}\to\infty}}{\left({3}{x}-{x}\right)}=\lim_{{{x}\to\infty}}{2}{x}=\infty$$$.
Let $$${f{{\left({x}\right)}}}={x}+{5}$$$ and $$${g{{\left({x}\right)}}}={x}$$$. Clearly $$$\lim_{{{x}\to\infty}}{\left({x}+{5}\right)}=\infty$$$ and $$$\lim_{{{x}\to\infty}}{x}=\infty$$$. Then $$$\lim_{{{x}\to\infty}}{\left({f{{\left({x}\right)}}}-{g{{\left({x}\right)}}}\right)}=\lim_{{{x}\to\infty}}{\left({x}+{5}-{x}\right)}=\lim_{{{x}\to\infty}}{5}={5}$$$.
So we can't find limit of difference without knowing functions.
To characterize this special case we say that when $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\infty$$$ and $$$\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}=\infty$$$, expression $$$\lim_{{{x}\to{a}}}{\left({\left({f{{\left({x}\right)}}}\right)}-{\left({g{{\left({x}\right)}}}\right)}\right)}$$$ is indeterminate form of type $$$\infty-\infty$$$.
So, we have seen four types of indeterminate forms. In these cases we need to know sequences $$${f{{\left({x}\right)}}}$$$ and $$${g{{\left({x}\right)}}}$$$. To get rid of indetermination it is often useful to perform algebraic manipulations. Now, let's go through a couple of examples.
Example 1. Find $$$\lim_{{{x}\to\infty}}{\left({3}{{x}}^{{2}}-{5}{x}\right)}$$$.
Since $$$\lim_{{{x}\to\infty}}{3}{{x}}^{{2}}=\infty$$$ and $$$\lim_{{{x}\to\infty}}{5}{x}=\infty$$$ we have indeterminate form of type $$$\infty-\infty$$$.
To handle it, let's perform algebraic manipulations: $$${3}{{x}}^{{2}}-{5}{x}={{x}}^{{2}}{\left({3}-\frac{{5}}{{x}}\right)}$$$.
Now, since $$$\lim_{{{x}\to\infty}}{{x}}^{{2}}=\infty$$$ and $$$\lim_{{{x}\to\infty}}{\left({3}-\frac{{5}}{{x}}\right)}={3}$$$ then their product is also very large number: $$$\lim_{{{x}\to\infty}}{\left({3}{{x}}^{{2}}-{5}{x}\right)}=\infty$$$.
Example 2. Find $$$\lim_{{{x}\to\infty}}{\left(-{4}{{x}}^{{3}}+{5}{{x}}^{{2}}\right)}$$$.
Since $$$\lim_{{{x}\to\infty}}-{4}{{x}}^{{3}}=-\infty$$$ and $$$\lim_{{{x}\to\infty}}{5}{{x}}^{{2}}=\infty$$$ we have indeterminate form of type $$$\infty-\infty$$$.
To handle it, let's perform algebraic manipulations: $$$-{4}{{x}}^{{2}}+{5}{{x}}^{{2}}={{x}}^{{3}}{\left(-{4}+\frac{{5}}{{x}}\right)}$$$.
Now, since $$$\lim_{{{x}\to\infty}}{{x}}^{{3}}=\infty$$$ and $$$\lim_{{{x}\to\infty}}{\left(-{4}+\frac{{5}}{{x}}\right)}=-{4}$$$ then $$$\lim_{{{x}\to\infty}}{\left(-{4}{{x}}^{{3}}+{5}{x}\right)}=-\infty$$$.
Example 3. Find $$$\lim_{{{x}\to\infty}}{\left({a}_{{0}}{{x}}^{{k}}+{a}_{{1}}{{x}}^{{{k}-{1}}}+\ldots+{a}_{{{k}-{1}}}{x}+{a}_{{k}}\right)}$$$, where $$${a}_{{0}},{a}_{{1}},\ldots{a}_{{k}}$$$ are constants.
This is generalization of above two examples. If all coefficients $$${a}_{{0}},{a}_{{1}},\ldots,{a}_{{k}}$$$ have same sign then limit of this sequence is $$$\infty$$$ (or $$$-\infty$$$). But if coeffcients have different signs then we have indeterminate form of type $$$\infty-\infty$$$.
To handle it, let's perform algebraic manipulations: $$${a}_{{0}}{{x}}^{{k}}+{a}_{{1}}{{x}}^{{{k}-{1}}}+\ldots+{a}_{{{k}-{1}}}{x}+{a}_{{k}}={{x}}^{{k}}{\left({a}_{{0}}+\frac{{{a}_{{1}}}}{{x}}+\ldots+\frac{{{a}_{{{k}-{1}}}}}{{{{x}}^{{{k}-{1}}}}}+\frac{{{a}_{{k}}}}{{{{x}}^{{k}}}}\right)}$$$.
Now, since $$${{x}}^{{k}}\to\infty$$$ and $$${a}_{{0}}+\frac{{{a}_{{1}}}}{{x}}+\ldots+\frac{{{a}_{{{k}-{1}}}}}{{{{x}}^{{{k}-{1}}}}}+\frac{{{a}_{{k}}}}{{{x}}^{{k}}}\to{a}_{{0}}$$$ as $$${x}\to\infty$$$, then $$${a}_{{0}}{{x}}^{{k}}+{a}_{{1}}{{x}}^{{{k}-{1}}}+\ldots+{a}_{{{k}-{1}}}{x}+{a}_{{k}}\to\infty$$$ if $$${a}_{{0}}>{0}$$$ and $$${x}_{{n}}\to-\infty$$$ if $$${a}_{{0}}<{0}$$$.
Example 4. Find $$$\lim_{{{x}\to\infty}}\frac{{{3}{{x}}^{{2}}-{5}{x}}}{{{7}{x}+{3}}}$$$.
Since $$$\lim_{{{x}\to\infty}}{\left({3}{{x}}^{{2}}-{5}{x}\right)}\to\infty$$$ and $$$\lim_{{{x}\to\infty}}{\left({7}{x}+{3}\right)}\to\infty$$$ we have indeterminate form of type $$$\frac{{\infty}}{{\infty}}$$$.
To handle it, let's perform algebraic manipulations. Factor out $$${x}$$$ raised to the greatest degree in numerator and denominator (in this case $$${{x}}^{{2}}$$$): $$$\frac{{{3}{{x}}^{{2}}-{5}{x}}}{{{7}{x}+{3}}}=\frac{{{{x}}^{{2}}{\left({3}-\frac{{5}}{{x}}\right)}}}{{{{x}}^{{2}}{\left(\frac{{7}}{{x}}+\frac{{3}}{{{x}}^{{2}}}\right)}}}=\frac{{{3}-\frac{{5}}{{{x}}^{{2}}}}}{{\frac{{7}}{{x}}+\frac{{3}}{{{x}}^{{2}}}}}$$$.
Now, since $$${3}-\frac{{5}}{{x}}\to{3}$$$ and $$$\frac{{7}}{{x}}+\frac{{3}}{{{x}}^{{2}}}\to{0}$$$ as $$${x}\to\infty$$$, then $$$\frac{{{3}-\frac{{5}}{{{x}}^{{2}}}}}{{\frac{{7}}{{x}}+\frac{{3}}{{{x}}^{{2}}}}}\to\infty$$$.
Example 5. Let $$$\lim_{{{x}\to\infty}}\frac{{{6}{{x}}^{{4}}-{3}{{x}}^{{2}}}}{{{8}{{x}}^{{7}}+{3}{x}}}$$$.
Since $$$\lim_{{{x}\to\infty}}{\left({6}{{x}}^{{4}}-{3}{{x}}^{{2}}\right)}\to\infty$$$ and $$$\lim_{{{x}\to\infty}}{\left({8}{{x}}^{{7}}+{3}{x}\right)}\to\infty$$$ we have indeterminate form of type $$$\frac{{\infty}}{{\infty}}$$$.
To handle it, let's perform algebraic manipulations. Factor out $$${x}$$$ raised to the greatest degree in numerator and denominator (in this case $$${{x}}^{{7}}$$$): $$$\frac{{{6}{{x}}^{{4}}-{3}{{x}}^{{2}}}}{{{8}{{x}}^{{7}}+{3}{x}}}=\frac{{{{x}}^{{7}}{\left(\frac{{6}}{{{x}}^{{3}}}-\frac{{3}}{{{x}}^{{5}}}\right)}}}{{{{x}}^{{7}}{\left({8}+\frac{{3}}{{{x}}^{{6}}}\right)}}}=\frac{{\frac{{6}}{{{x}}^{{3}}}-\frac{{3}}{{{x}}^{{5}}}}}{{{8}+\frac{{3}}{{{x}}^{{6}}}}}$$$.
Now, since $$$\frac{{6}}{{{x}}^{{3}}}-\frac{{3}}{{{x}}^{{5}}}\to{0}$$$ and $$${8}+\frac{{3}}{{{x}}^{{6}}}\to{8}$$$ as $$${x}\to\infty$$$, then $$$\lim_{{{x}\to\infty}}\frac{{\frac{{6}}{{{x}}^{{3}}}-\frac{{3}}{{{x}}^{{5}}}}}{{{8}+\frac{{3}}{{{x}}^{{6}}}}}\to{0}$$$.
Example 6. Find $$$\lim_{{{x}\to\infty}}\frac{{{3}{{x}}^{{2}}-{5}{x}}}{{{7}{{x}}^{{2}}+{3}}}$$$.
Since $$$\lim_{{{x}\to\infty}}{\left({3}{{x}}^{{2}}-{5}{x}\right)}=\infty$$$ and $$$\lim_{{{x}\to\infty}}{\left({7}{{x}}^{{2}}+{3}\right)}=\infty$$$ we have indeterminate form of type $$$\frac{{\infty}}{{\infty}}$$$.
To handle it, let's perform algebraic manipulations. Factor out $$${x}$$$ raised to the greatest degree in numerator and denominator (in this case $$${{x}}^{{2}}$$$) $$$\frac{{{3}{{x}}^{{2}}-{5}{x}}}{{{7}{{x}}^{{2}}+{3}}}=\frac{{{{x}}^{{2}}{\left({3}-\frac{{5}}{{x}}\right)}}}{{{{n}}^{{2}}{\left({7}+\frac{{3}}{{{x}}^{{2}}}\right)}}}=\frac{{{3}-\frac{{5}}{{x}}}}{{{7}+\frac{{3}}{{{x}}^{{2}}}}}$$$.
Now, since $$${3}-\frac{{5}}{{x}}\to{3}$$$ and $$${7}+\frac{{3}}{{{x}}^{{2}}}\to{7}$$$ as $$${x}\to\infty$$$, then $$$\lim_{{{x}\to\infty}}\frac{{{3}-\frac{{5}}{{x}}}}{{{7}+\frac{{3}}{{{x}}^{{2}}}}}=\frac{{3}}{{7}}$$$.
Example 7. Find $$$\lim_{{{x}\to\infty}}\frac{{{a}_{{0}}{{x}}^{{k}}+{a}_{{1}}{{x}}^{{{k}-{1}}}+\ldots+{a}_{{{k}-{1}}}{x}+{a}_{{k}}}}{{{b}_{{0}}{{x}}^{{m}}+{b}_{{1}}{{x}}^{{{m}-{1}}}+..+{b}_{{{m}-{1}}}{x}+{b}_{{m}}}}$$$ where $$${a}_{{0}},{a}_{{1}},\ldots,{a}_{{k}}$$$ and $$${b}_{{0}},{b}_{{1}},\ldots,{b}_{{m}}$$$ are constants.
This is generalization of above three examples. We have indeterminate form of type $$$\frac{{\infty}}{{\infty}}$$$.
To handle it, let's perform algebraic manipulations. Factor out $$${{x}}^{{k}}$$$ from numerator and $$${{x}}^{{m}}$$$ from denominator: $$$\frac{{{a}_{{0}}{{x}}^{{k}}+{a}_{{1}}{{x}}^{{{k}-{1}}}+\ldots+{a}_{{{k}-{1}}}{x}+{a}_{{k}}}}{{{b}_{{0}}{{x}}^{{m}}+{b}_{{1}}{{x}}^{{{m}-{1}}}+\ldots+{b}_{{{m}-{1}}}{x}+{b}_{{m}}}}=\frac{{{{x}}^{{k}}{\left({a}_{{0}}+\frac{{{a}_{{1}}}}{{x}}+\ldots+\frac{{{a}_{{k}}}}{{{{x}}^{{k}}}}\right)}}}{{{{x}}^{{m}}{\left({b}_{{0}}+\frac{{{b}_{{1}}}}{{x}}+\ldots+\frac{{{b}_{{m}}}}{{{{x}}^{{m}}}}\right)}}}={{x}}^{{{k}-{m}}}{\left(\frac{{{a}_{{0}}+\frac{{{a}_{{1}}}}{{x}}+\ldots+\frac{{{a}_{{k}}}}{{{{x}}^{{k}}}}}}{{{b}_{{0}}+\frac{{{b}_{{1}}}}{{x}}+\ldots+\frac{{{b}_{{m}}}}{{{{x}}^{{m}}}}}}\right)}$$$.
Second factor has limit $$$\frac{{a}_{{0}}}{{b}_{{0}}}$$$. If $$${k}={m}$$$ then $$${{x}}^{{{k}-{m}}}={1}\to{1}$$$ and required limit approaches $$$\frac{{{a}_{{0}}}}{{{b}_{{0}}}}$$$. If $$${k}>{m}$$$ then $$${{x}}^{{{k}-{m}}}\to\infty$$$ and required limit approaches $$$\infty$$$ (or $$$-\infty$$$, sign depends on sign of $$$\frac{{{a}_{{0}}}}{{{b}_{{0}}}}$$$). If $$${k}<{m}$$$ then $$${{x}}^{{{k}-{m}}}\to{0}$$$ and required limit approaches $$${0}$$$.
Example 8. Find $$$\lim_{{{x}\to\infty}}\sqrt{{{x}}}{\left(\sqrt{{{x}+{1}}}-\sqrt{{{x}}}\right)}$$$.
We can rewrite it as $$$\lim_{{{x}\to\infty}}{\left(\sqrt{{{x}}}\sqrt{{{x}+{1}}}-\sqrt{{{x}}}\sqrt{{{x}}}\right)}=\lim_{{{x}\to\infty}}{\left(\sqrt{{{{x}}^{{2}}+{x}}}-{x}\right)}$$$.
This indeterminate form of type $$$\infty-\infty$$$.
When we deal with radicals, we need to multiply both numerator and denominator by conjugate radical. Here we multiply both numerator and denominator by $$$\sqrt{{{{x}}^{{2}}+{x}}}+{x}$$$:
$$$\sqrt{{{{x}}^{{2}}+{x}}}-{x}=\frac{{{\left(\sqrt{{{{x}}^{{2}}+{x}}}-{x}\right)}{\color{red}{{{\left(\sqrt{{{{x}}^{{2}}+{x}}}+{x}\right)}}}}}}{{{\color{red}{{\sqrt{{{{x}}^{{2}}+{x}}}+\sqrt{{{x}}}}}}}}=\frac{{{{\left(\sqrt{{{{x}}^{{2}}+{x}}}\right)}}^{{2}}-{{x}}^{{2}}}}{{\sqrt{{{{x}}^{{2}}+{x}}}+\sqrt{{{x}}}}}=\frac{{{{x}}^{{2}}+{x}-{{x}}^{{2}}}}{{\sqrt{{{{x}}^{{2}}+{x}}}+{x}}}=$$$
$$$=\frac{{{x}}}{{\sqrt{{{{x}}^{{2}}+{x}}}+{x}}}$$$.
Now, factor out $$${x}$$$: $$$\frac{{x}}{{\sqrt{{{{x}}^{{2}}+{x}}}+{x}}}={\left(\frac{{x}}{{{x}{\left(\sqrt{{{1}+\frac{{1}}{{x}}}}+{1}\right)}}}\right)}=\frac{{1}}{{\sqrt{{{1}+\frac{{1}}{{x}}}}-{1}}}$$$.
Since $$${1}<\sqrt{{{1}+\frac{{1}}{{x}}}}<{1}+\frac{{1}}{{x}}$$$ for large $$${x}$$$ and $$${1}+\frac{{1}}{{x}}\to{1}$$$ as $$${x}\to\infty$$$ then by Squeeze Theorem $$$\sqrt{{{1}+\frac{{1}}{{x}}}}\to{1}$$$.
That's why $$$\lim_{{{x}\to\infty}}{\left(\sqrt{{{{x}}^{{2}}+{x}}}-{x}\right)}=\lim_{{{x}\to\infty}}{\left(\frac{{1}}{{\sqrt{{{1}+\frac{{1}}{{x}}}}-{1}}}\right)}=\frac{{1}}{{{1}+{1}}}=\frac{{1}}{{2}}$$$.
Now, we will calculate limit that we will need later.
Example 9. Find $$$\lim_{{{x}\to{0}}}\frac{{{\sin{{\left({x}\right)}}}}}{{x}}$$$.
As $$${x}\to{0}$$$ $$${\sin{{\left({x}\right)}}}\to{0}$$$, so we have indeterminate form of type $$$\frac{{0}}{{0}}$$$.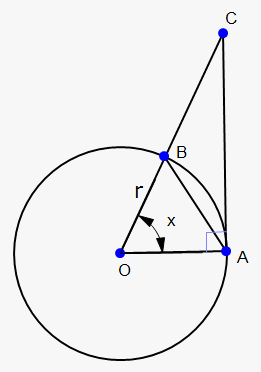
Before finding this limit we need to prove that for $$${0}<{x}<\frac{\pi}{{2}}$$$ we have that $$${\sin{{\left({x}\right)}}}<{x}<{\tan{{\left({x}\right)}}}$$$.
For this consider circle with radius $$${r}$$$, tangent $$${A}{C}$$$ to circle and central angle $$${x}$$$.
Clearly area of triangle AOB is less than area of sector AOB, and area of sector AOB is less than area of triangle AOC.
We have that area of sector AOB is $$$\frac{{{x}}}{{{2}\pi}}\cdot\pi{{r}}^{{2}}=\frac{{1}}{{2}}{{r}}^{{2}}{x}$$$.
Since area of triangle AOB is $$$\frac{{1}}{{2}}{{r}}^{{2}}{\sin{{\left({x}\right)}}}$$$, area of sector AOB is $$$\frac{{1}}{{2}}{{r}}^{{2}}{x}$$$ and area of triangle AOC is $$$\frac{{1}}{{2}}{{r}}^{{2}}{\tan{{\left({x}\right)}}}$$$ then $$$\frac{{1}}{{2}}{{r}}^{{2}}{\sin{{\left({x}\right)}}}<\frac{{1}}{{2}}{{r}}^{{2}}{x}<\frac{{1}}{{2}}{{r}}^{{2}}{\tan{{\left({x}\right)}}}$$$ or $$${\sin{{\left({x}\right)}}}<{x}<{\tan{{\left({x}\right)}}}$$$.
Now, since $$${0}<{x}<\frac{\pi}{{2}}$$$ then we can divide $$${\sin{{\left({x}\right)}}}$$$ by each member of inequality (don't forget to invert inequality signs): $$$\frac{{{\sin{{\left({x}\right)}}}}}{{{\color{red}{{{\sin{{\left({x}\right)}}}}}}}}>\frac{{{\sin{{\left({x}\right)}}}}}{{{\color{red}{{{x}}}}}}>\frac{{{\sin{{\left({x}\right)}}}}}{{{\color{red}{{{\tan{{\left({x}\right)}}}}}}}}$$$ or $$${1}>\frac{{{\sin{{\left({x}\right)}}}}}{{x}}>{\cos{{\left({x}\right)}}}$$$.
Thus, we obtained that $$${\cos{{\left({x}\right)}}}<\frac{{{\sin{{\left({x}\right)}}}}}{{x}}<{1}$$$.
As $$${x}\to{0}$$$ $$${\cos{{\left({x}\right)}}}\to{1}$$$ that's why $$$\lim_{{{x}\to{0}}}{\cos{{\left({x}\right)}}}={1}$$$, so, by Squeeze Theorem $$$\lim_{{{x}\to{{0}}^{+}}}\frac{{{\sin{{\left({x}\right)}}}}}{{x}}={1}$$$. (we wrote one-sided limit because we considered interval $$${\left({0},\frac{\pi}{{2}}\right)}$$$). Since $$$\frac{{{\sin{{\left({x}\right)}}}}}{{x}}$$$ is even function then also $$$\lim_{{{x}\to{{0}}^{{-}}}}\frac{{{\sin{{\left({x}\right)}}}}}{{x}}={1}$$$. Since one-sided limits are equal then $$$\lim_{{{x}\to{0}}}\frac{{{\sin{{\left({x}\right)}}}}}{{x}}={1}$$$.
From this limit we can find other limits.
Example 10. Find $$$\lim_{{{x}\to{0}}}\frac{{{1}-{\cos{{\left({x}\right)}}}}}{{{x}}^{{2}}}$$$.
Here we have indeterminate form of type $$$\frac{{0}}{{0}}$$$.
Since $$${1}-{\cos{{\left({x}\right)}}}={2}{{\sin}}^{{2}}{\left(\frac{{x}}{{2}}\right)}$$$ then $$$\frac{{{1}-{\cos{{\left({x}\right)}}}}}{{{x}}^{{2}}}=\frac{{{2}{{\sin}}^{{2}}{\left(\frac{{x}}{{2}}\right)}}}{{{x}}^{{2}}}=\frac{{1}}{{2}}\frac{{{{\sin}}^{{2}}{\left(\frac{{x}}{{2}}\right)}}}{{\frac{{{{x}}^{{2}}}}{{4}}}}=\frac{{1}}{{2}}{{\left(\frac{{{\sin{{\left(\frac{{x}}{{2}}\right)}}}}}{{\frac{{x}}{{2}}}}\right)}}^{{2}}$$$.
Since $$${x}\to{0}$$$ then $$$\frac{{x}}{{2}}\to{0}$$$ and so $$$\lim_{{{x}\to{0}}}\frac{{{\sin{{\left(\frac{{x}}{{2}}\right)}}}}}{{\frac{{x}}{{2}}}}={1}$$$.
Thus, $$$\lim_{{{x}\to{0}}}\frac{{{1}-{\cos{{\left({x}\right)}}}}}{{{x}}^{{2}}}=\lim_{{{x}\to{0}}}\frac{{1}}{{2}}{{\left(\frac{{{\sin{{\left(\frac{{x}}{{2}}\right)}}}}}{{\frac{{x}}{{2}}}}\right)}}^{{2}}=\frac{{1}}{{2}}{{\left(\lim_{{{x}\to{0}}}\frac{{{\sin{{\left(\frac{{x}}{{2}}\right)}}}}}{{\frac{{x}}{{2}}}}\right)}}^{{2}}=\frac{{1}}{{2}}\cdot{{1}}^{{2}}=\frac{{1}}{{2}}$$$.
When we talked about the number $$$e$$$, we proved that the sequence $$${x}_{{n}}={{\left({1}+\frac{{1}}{{n}}\right)}}^{{n}}$$$ has limit $$$e$$$.
We have same thing for functions and formulate it as following fact:
Fact. $$$\lim_{{{x}\to\infty}}{{\left({1}+\frac{{1}}{{x}}\right)}}^{{x}}={e}$$$, $$$\lim_{{{x}\to-\infty}}{{\left({1}+\frac{{1}}{{x}}\right)}}^{{x}}={e}$$$.
If we make substitution $$${t}=\frac{{1}}{{x}}$$$ then $$${t}\to{0}$$$ as $$${x}\to\infty$$$. Thus, $$$\lim_{{{t}\to{0}}}{{\left({1}+{t}\right)}}^{{\frac{{1}}{{t}}}}={e}$$$.
Example 11. Prove that $$$\lim_{{{h}\to{0}}}\frac{{{{a}}^{{h}}-{1}}}{{h}}={\ln{{\left({a}\right)}}}$$$.
Let $$${{a}}^{{h}}-{1}={x}$$$ then $$${x}\to{0}$$$ as $$${h}\to{0}$$$. And $$${h}={\log}_{{a}}{\left({x}+{1}\right)}=\frac{{\ln{{\left({x}+{1}\right)}}}}{{\ln{{\left({a}\right)}}}}$$$
So, $$$\lim_{{{h}\to{0}}}\frac{{{{a}}^{{h}}-{1}}}{{h}}=\lim_{{{x}\to{0}}}\frac{{x}}{{\frac{{{\ln{{\left({x}+{1}\right)}}}}}{{{\ln{{\left({a}\right)}}}}}}}={\ln{{\left({a}\right)}}}\lim_{{{x}\to{0}}}\frac{{x}}{{{\ln{{\left({x}+{1}\right)}}}}}={\ln{{\left({a}\right)}}}\lim_{{{x}\to{0}}}\frac{{1}}{{\frac{{1}}{{x}}{\ln{{\left({x}+{1}\right)}}}}}=$$$
$$$={\ln{{\left({a}\right)}}}\lim_{{{x}\to{0}}}\frac{{1}}{{{{\ln{{\left({1}+{x}\right)}}}}^{{\frac{{1}}{{x}}}}}}={\ln{{\left({a}\right)}}}\frac{{1}}{{{\ln{{\left(\lim_{{{x}\to{0}}}{{\left({1}+{x}\right)}}^{{\frac{{1}}{{x}}}}\right)}}}}}={\ln{{\left({a}\right)}}}\frac{{1}}{{{\ln{{\left({e}\right)}}}}}={\ln{{\left({a}\right)}}}\frac{{1}}{{1}}={\ln{{\left({a}\right)}}}$$$
Now, suppose that $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={L}$$$ and $$$\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}={M}$$$. We want to find $$$\lim_{{{x}\to{a}}}{{f{{\left({x}\right)}}}}^{{{g{{\left({x}\right)}}}}}$$$.
To handle it we use continuity of the natural logarithm: let $$$\lim_{{{x}\to{a}}}{{f{{\left({x}\right)}}}}^{{{g{{\left({x}\right)}}}}}={B}$$$ then $$${\ln{{\left(\lim_{{{x}\to{a}}}{{f{{\left({x}\right)}}}}^{{{g{{\left({x}\right)}}}}}\right)}}}={\ln{{\left({B}\right)}}}$$$.
This can be rewritten as $$$\lim_{{{x}\to{a}}}{\ln{{\left({{f{{\left({x}\right)}}}}^{{{g{{\left({x}\right)}}}}}\right)}}}={\ln{{\left({B}\right)}}}$$$ or $$$\lim_{{{x}\to{a}}}{\left({g{{\left({x}\right)}}}{\ln{{\left({f{{\left({x}\right)}}}\right)}}}\right)}={\ln{{\left({B}\right)}}}$$$.
Again using continuity of the function we can write that $$$\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}\cdot{\ln{{\left(\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}\right)}}}={\ln{{\left({B}\right)}}}$$$.
So, $$${\ln{{\left({B}\right)}}}={M}{\ln{{\left({L}\right)}}}$$$ or $$${B}={{L}}^{{M}}$$$.
We can always find this limit except three indeterminate cases:
- $$${L}={1}$$$, $$${M}=\pm\infty$$$. In this case $$${M}{\ln{{\left({L}\right)}}}$$$ is indeterminate form of type $$$\infty\cdot{0}$$$.
- $$${L}={0}$$$, $$${M}={0}$$$. In this case $$${M}{\ln{{\left({L}\right)}}}$$$ is indeterminate form of type $$${0}\cdot\infty$$$.
- $$${L}=+\infty$$$, $$${M}={0}$$$. In this case $$${M}{\ln{{\left({L}\right)}}}$$$ is indeterminate form of type $$${0}\cdot\infty$$$.
Example 12. Find $$$\lim_{{{x}\to{0}}}{{x}}^{{x}}$$$.
Since $$$\lim_{{{x}\to{0}}}{x}={0}$$$ then we have case b) here.
Let $$${B}={{x}}^{{x}}$$$ then $$${\ln{{\left({B}\right)}}}={\ln{{\left({{x}}^{{x}}\right)}}}={x}{\ln{{\left({x}\right)}}}$$$.
It is known that $$$\lim_{{{x}\to{0}}}{x}{\ln{{\left({x}\right)}}}={0}$$$ that's why $$${\ln{{\left({B}\right)}}}={0}$$$ or $$${B}={1}$$$.
Thus, $$$\lim_{{{x}\to{0}}}{{x}}^{{x}}={1}$$$.
