Limits Involving Infinity

Now it is time to talk about the limits that involve the special symbol $\infty$ .

First, we are going to talk about infinite limits.

Definition. We write that $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\infty$ $\left(\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=-\infty\right)$ if for any ${E}>{0}$ there exists $\delta>{0}$ such that ${f{{\left({x}\right)}}}>{E}\ {\left({f{{\left({x}\right)}}}<-{E}\right)}$ when ${\left|{x}-{a}\right|}<\delta$ .

This definition says that $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\infty$ means the following: when ${x}$ approaches ${a}$ , ${f{{\left({x}\right)}}}$ increases (decreases) without a bound and can take a very large number.

Once again, the symbol $\infty$ is just used to denote a very large number. We can't perform arithmetic operations on such numbers.

Note: we assume that $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\infty$ exists, i.e. ${f{{\left({x}\right)}}}$ approaches a very large number (infinity) denoted by $\infty$ . Unlike it, $\lim_{{{x}\to{0}}}{\sin{{\left(\frac{{1}}{{x}}\right)}}}$ doesn't exist, because the function doesn't approach any value.

So, we use the symbol $\infty$ to denote the fact that the function approaches a very large number, not the fact that the limit doesn't exist, i.e. the function doesn't approach any number.

Example 1. Find $\lim_{{{x}\to{0}}}\frac{{1}}{{{x}}^{{2}}}$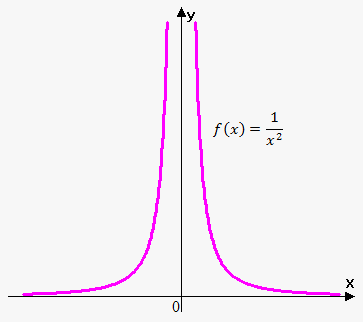 . infinite limits

When ${x}$ approaches $0$ , ${{x}}^{{2}}$ also approaches $0$ ; so, $\frac{{1}}{{{x}}^{{2}}}$ approaches a very large value (for example, $\frac{{1}}{{{\left({0.001}\right)}}^{{2}}}={1000000}$ ). Thus, $\lim_{{{x}\to{0}}}=\frac{{1}}{{{x}}^{{2}}}$ .

Also, it can be seen easily that $\lim_{{{x}\to{0}}}-\frac{{1}}{{{x}}^{{2}}}=-\infty$ .

Similarly, we can define infinite one-sided limits: $\lim_{{{x}\to{{a}}^{{-}}}}{f{{\left({x}\right)}}}=\infty$ , $\lim_{{{x}\to{{a}}^{+}}}{f{{\left({x}\right)}}}=\infty$ , $\lim_{{{x}\to{{a}}^{{-}}}}{f{{\left({x}\right)}}}=-\infty$ , $\lim_{{{x}\to{{a}}^{+}}}{f{{\left({x}\right)}}}=-\infty$ .

Example 2. Find $\lim_{{{x}\to{1}}}\frac{{1}}{{{x}-{1}}}$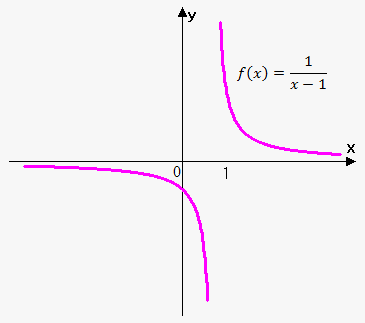 . infinite one sided limits

When we approach $1$ from the left, ${x}-{1}$ is a small positive number and $\frac{{1}}{{{x}-{1}}}$ is a large negative number. Therefore, $\lim_{{{x}\to{{1}}^{{-}}}}\frac{{1}}{{{x}-{1}}}=-\infty$ .

When we approach $1$ from the right, ${x}-{1}$ is a small positive number and $\frac{{1}}{{{x}-{1}}}$ is a large positive number. Therefore, $\lim_{{{x}\to{{1}}^{+}}}\frac{{1}}{{{x}-{1}}}=\infty$ .

Since $\lim_{{{x}\to{{1}}^{{-}}}}\frac{{1}}{{{x}-{1}}}\ne\lim_{{{x}\to{{1}}^{+}}}\frac{{1}}{{{x}-{1}}}$ , we can say that $\lim_{{{x}\to{1}}}\frac{{1}}{{{x}-{1}}}$ doesn't exist.

Limits at Infinity

Above, we let ${x}$ approach some number, and the result was that the values of ${f{{\left({x}\right)}}}$ became arbitrarily large (positive or negative).

Now, we let ${x}$ become arbitrarily large (positive or negative) and see what happens to ${f{{\left({x}\right)}}}$ .

Example 3. Find $\lim_{{{x}\to\infty}}\frac{{{3}{{x}}^{{2}}-{1}}}{{{{x}}^{{2}}+{1}}}$ by guessing.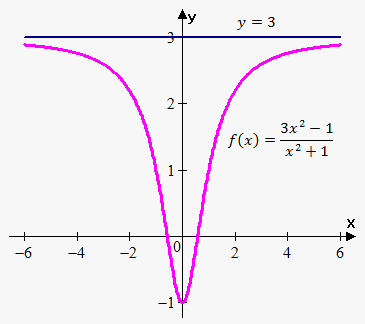 limits at infinity

If ${x}={100}$ , we have that ${f{{\left({100}\right)}}}=\frac{{{3}\cdot{{100}}^{{2}}-{1}}}{{{{100}}^{{2}}+{1}}}\approx{2.9996}$ , and if ${x}={1000}$ , it can be said that ${f{{\left({1000}\right)}}}=\frac{{{3}\cdot{{1000}}^{{2}}-{1}}}{{{{1000}}^{{2}}+{1}}}\approx{2.999996}$ .

As ${x}$ grows larger and larger, the values of ${f{{\left({x}\right)}}}$ become closer and closer to $3$ .

We can make ${f{{\left({x}\right)}}}$ as close to $3$ as we like by choosing a suffciently large ${x}$ .

Thus, $\lim_{{{x}\to\infty}}\frac{{{3}{{x}}^{{2}}-{1}}}{{{{x}}^{{2}}+{1}}}={3}$ .

Similarly, we can show that $\lim_{{{x}\to-\infty}}\frac{{{3}{{x}}^{{2}}-{1}}}{{{{x}}^{{2}}+{1}}}={3}$ .

Definition. We say that $\lim_{{{x}\to\infty}}{f{{\left({x}\right)}}}={L}\ {\left(\lim_{{{x}\to-\infty}}{f{{\left({x}\right)}}}={L}\right)}$ if for every number $\epsilon>{0}$ there exists a number ${M}>{0}$ such that ${\left|{f{{\left({x}\right)}}}-{L}\right|}<\epsilon$ when ${x}>{M}\ {\left({x}<-{M}\right)}$ .

This means that we can make ${f{{\left({x}\right)}}}$ as close as we like to ${L}$ by taking a sufficiently large ${x}$ (positive or negative).

Example 4. Find $\lim_{{{x}\to\infty}}\frac{{1}}{{{x}-{1}}}$ and $\lim_{{{x}\to-\infty}}\frac{{1}}{{{x}-{1}}}$ .

Observe that when ${x}$ is large, $\frac{{1}}{{{x}-{1}}}$ is small. Therefore, we can make $\frac{{1}}{{{x}-{1}}}$ as close to $0$ as we like by taking a sufficiently large ${x}$ (positive or negative). Therefore, $\lim_{{{x}\to\infty}}\frac{{1}}{{{x}-{1}}}=\lim_{{{x}\to-\infty}}\frac{{1}}{{{x}-{1}}}={0}$ . You can see the graph of the function in example 2.

Let's run through another quick example.

Example 5. Evaluate $\lim_{{{x}\to{{0}}^{{-}}}}{{e}}^{{\frac{{1}}{{x}}}}$ .

Let ${t}=\frac{{1}}{{x}}$ ; then, ${t}\to-\infty$ as ${x}\to{{0}}^{{-{}}}$ . Therefore, $\lim_{{{x}\to{{0}}^{{-}}}}{{e}}^{{\frac{{1}}{{x}}}}=\lim_{{{t}\to-\infty}}{{e}}^{{t}}={0}$ .

Again, note that $\infty$ is not a number, it is just a way to show that some value increases (or decreases) without a bound.

Let's do another example.

Example 6. Find $\lim_{{{x}\to\infty}}{\cos{{\left({x}\right)}}}$ .

As ${x}$ increases, the value of ${\cos{{\left({x}\right)}}}$ oscillates infinitely many times between $-1$ and $1$ . Thus, $\lim_{{{x}\to\infty}}{\cos{{\left({x}\right)}}}$ doesn't exist.

Infinite Limits at Infinity

The notation $\lim_{{{x}\to\infty}}{f{{\left({x}\right)}}}=\infty$ means that ${f{{\left({x}\right)}}}$ becomes large as ${x}$ becomes large. The following notations have a similar meaning: $\lim_{{{x}\to-\infty}}{f{{\left({x}\right)}}}=\infty$ , $\lim_{{{x}\to\infty}}{f{{\left({x}\right)}}}=-\infty$ , $\lim_{{{x}\to-\infty}}{f{{\left({x}\right)}}}=-\infty$ .

For example, $\lim_{{{x}\to\infty}}{{e}}^{{x}}=\infty$ , $\lim_{{{x}\to-\infty}}{{x}}^{{2}}=\infty$ , $\lim_{{{x}\to\infty}}-{{e}}^{{x}}=-\infty$ , and $\lim_{{{x}\to-\infty}}{{x}}^{{3}}=-\infty$ .

Most of the properties of the limits hold for infinite limits. Now, let's formulate a couple of laws involving infinity.

Properties of Infinite Limits

Suppose that ${a}$ is a number (it can be infinity) and ${L}$ is a finite number.

Law 1. If $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={L}$ and $\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}=\infty$ , then $\lim_{{{x}\to{a}}}{\left({f{{\left({x}\right)}}}+{g{{\left({x}\right)}}}\right)}=\infty$ .

Law 2. If $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={L}$ and $\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}=\infty$ , then $\lim_{{{x}\to{a}}}{\left({f{{\left({x}\right)}}}-{g{{\left({x}\right)}}}\right)}=-\infty$ .

Law 3. If $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={L}\ne{0}$ and $\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}=\infty$ , then $\lim_{{{x}\to{a}}}{\left({f{{\left({x}\right)}}}{g{{\left({x}\right)}}}\right)}=\infty$ if ${L}>{0}$ and $-\infty$ if ${L}<{0}.$

Law 4. If $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={L}$ and $\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}=\pm\infty$ , then $\lim_{{{x}\to{a}}}{\left(\frac{{f{{\left({x}\right)}}}}{{g{{\left({x}\right)}}}}\right)}={0}$ .

Law 5. If $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={L}$ and $\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}=\infty$ , then $\lim_{{{x}\to{a}}}{\left(\frac{{{g{{\left({x}\right)}}}}}{{{f{{\left({x}\right)}}}}}\right)}=\infty$ if ${L}>{0}$ and $-\infty$ if ${L}<{0}$ .

Law 6. If $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\infty$ and $\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}=\infty$ , then $\lim_{{{x}\to{a}}}{\left({f{{\left({x}\right)}}}+{g{{\left({x}\right)}}}\right)}=\infty$ .

Law 7. If $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\infty$ and $\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}=-\infty$ , then $\lim_{{{x}\to{a}}}{\left({f{{\left({x}\right)}}}-{g{{\left({x}\right)}}}\right)}=\infty$ .

Law 8. If $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={L}\ne{0}$ and $\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}={0}$ , then $\lim_{{{x}\to{a}}}{\left(\frac{{f{{\left({x}\right)}}}}{{g{{\left({x}\right)}}}}\right)}=\infty$ if ${L}>{0}$ and $-\infty$ if ${L}<{0}$ .

Law 9. If $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={L}\ne{0}$ and $\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}={0}$ , then $\lim_{{{x}\to{a}}}{\left(\frac{{g{{\left({x}\right)}}}}{{f{{\left({x}\right)}}}}\right)}={0}$ .

Law 10. If $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\infty$ , then $\lim_{{{x}\to{a}}}{c}{f{{\left({x}\right)}}}=\infty$ , where ${c}\ne{0}$ is some constant.

Note that these properties also hold for one-sided limits.

It is easy to believe that these properties are true.

Indeed, although we can't perform arithmetic operations over infinite values, it is clear that the sum of large numbers is a large number again (Law 1); the product of large numbers is again a large number (Law 3); if we divide a large number by a very small number, we will obtain again a large number (Law 4), etc.

Example 7. Find $\lim_{{{x}\to{2^+}}}\frac{{{1}-{x}}}{{{x}-{2}}}$ .

Since $\lim_{{{x}\to{2^+}}}{\left({1}-{x}\right)}=-{1}$ and $\lim_{{{x}\to{2^+}}}{\left({x}-{2}\right)}={0}$ , according to Law 8, $\lim_{{{x}\to{2^+}}}\frac{{{1}-{x}}}{{{x}-{2}}}=-\infty$ .

And the final example.

Example 8. Find $\lim_{{{x}\to\infty}}\frac{{{1}-\frac{{1}}{{x}}}}{{{x}}}$ .

Since $\lim_{{{x}\to\infty}}{\left({1}-\frac{{1}}{{x}}\right)}={1}$ and $\lim_{{{x}\to\infty}}{x}=\infty$ , according to Law 4, $\lim_{{{x}\to\infty}}\frac{{{1}-\frac{{1}}{{x}}}}{{x}}={0}$ .