Taylor Polynomial
Suppose that we have n-th degree polynomial $$${p}{\left({x}\right)}={a}_{{0}}+{a}_{{1}}{\left({x}-{a}\right)}+{a}_{{2}}{{\left({x}-{a}\right)}}^{{2}}+\ldots+{a}_{{{n}-{1}}}{{\left({x}-{a}\right)}}^{{{n}-{1}}}+{a}_{{n}}{{\left({x}-{a}\right)}}^{{n}}$$$, where $$${a},{a}_{{0}},{a}_{{1}},{a}_{{2}},\ldots,{a}_{{n}}$$$ are constants.
Now, differentiate this polynomial $$${n}$$$ times:
$$${p}'{\left({x}\right)}={a}_{{1}}+{2}\cdot{a}_{{2}}{\left({x}-{a}\right)}+{3}\cdot{a}_{{3}}{{\left({x}-{a}\right)}}^{{2}}+\ldots+{\left({n}-{1}\right)}\cdot{a}_{{{n}-{1}}}{{\left({x}-{a}\right)}}^{{{n}-{2}}}+{n}\cdot{a}_{{n}}{{\left({x}-{a}\right)}}^{{{n}-{1}}}$$$,
$$${p}''{\left({x}\right)}={1}\cdot{2}\cdot{a}_{{2}}+{2}\cdot{3}\cdot{a}_{{3}}{\left({x}-{a}\right)}+\ldots+{\left({n}-{2}\right)}{\left({n}-{1}\right)}{a}_{{{n}-{1}}}{{\left({x}-{a}\right)}}^{{{n}-{3}}}+{\left({n}-{1}\right)}{n}{a}_{{n}}{{\left({x}-{a}\right)}}^{{{n}-{2}}}$$$,
$$${p}'''{\left({x}\right)}={1}\cdot{2}\cdot{3}\cdot{a}_{{3}}+\ldots+{\left({n}-{3}\right)}{\left({n}-{2}\right)}{\left({n}-{1}\right)}{a}_{{{n}-{1}}}{{\left({x}-{a}\right)}}^{{{n}-{4}}}+{\left({n}-{2}\right)}{\left({n}-{1}\right)}{n}{a}_{{n}}{{\left({x}-{a}\right)}}^{{{n}-{3}}}$$$,
$$$\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots$$$
$$${{p}}^{{{\left({n}\right)}}}{\left({x}\right)}={1}\cdot{2}\cdot{3}\cdot\ldots\cdot{n}\cdot{a}_{{n}}$$$.
If we now plug $$${a}$$$ instead of $$${x}$$$ in polynomial and all its derivatives we will obtain that
$$${p}{\left({a}\right)}={a}_{{0}}$$$, $$${p}'{\left({a}\right)}={a}_{{1}}$$$, $$${p}''{\left({a}\right)}={1}\cdot{2}\cdot{a}_{{2}}$$$, $$${p}'''{\left({a}\right)}={1}\cdot{2}\cdot{3}\cdot{a}_{{3}}$$$, ..., $$${{p}}^{{{\left({n}\right)}}}{\left({a}\right)}={1}\cdot{2}\cdot{3}\cdot\ldots\cdot{n}\cdot{a}_{{n}}$$$.
Since factorial of number is $$${n}!={1}\cdot{2}\cdot{3}\cdot\ldots\cdot{n}$$$ then
$$${a}_{{0}}={p}{\left({a}\right)}$$$, $$${a}_{{1}}=\frac{{{p}'{\left({a}\right)}}}{{{1}!}}$$$, $$${a}_{{2}}=\frac{{{p}''{\left({a}\right)}}}{{{2}!}}$$$, ..., $$${a}_{{n}}=\frac{{{{p}}^{{{\left({n}\right)}}}{\left({a}\right)}}}{{{n}!}}$$$.
If we now substitute expressions for constants into polynomial we will obtain Taylor Fomula.
Taylor Formula for Polynomials. Polynomial$$${p}{\left({x}\right)}={p}{\left({a}\right)}+\frac{{{p}'{\left({a}\right)}}}{{{1}!}}{\left({x}-{a}\right)}+\frac{{{p}''{\left({a}\right)}}}{{{2}!}}{{\left({x}-{a}\right)}}^{{2}}+\ldots+\frac{{{{p}}^{{{\left({n}-{1}\right)}}}{\left({a}\right)}}}{{{\left({n}-{1}\right)}!}}{{\left({x}-{a}\right)}}^{{{n}-{1}}}+\frac{{{{p}}^{{{\left({n}\right)}}}{\left({a}\right)}}}{{{n}!}}{{\left({x}-{a}\right)}}^{{n}}$$$. is called taylor polynomial at $$${x}={a}$$$.
With the help of Taylor formula we can write any polynomial in terms of $$${\left({x}-{a}\right)}$$$.
Example 1. Write polynomial $$${p}{\left({x}\right)}={{x}}^{{3}}+{3}{{x}}^{{2}}-{2}{x}+{1}$$$ in terms of $$${\left({x}-{2}\right)}$$$.
Here $$${a}={2}$$$.
We have that $$${p}'{\left({x}\right)}={3}{{x}}^{{2}}+{6}{x}-{2}$$$, $$${p}''{\left({x}\right)}={6}{x}+{6}$$$, $$${p}'''{\left({x}\right)}={6}$$$. All higher-order derivatives will equal 0.
Now, $$${p}{\left({2}\right)}={{2}}^{{3}}+{3}\cdot{{2}}^{{2}}-{2}\cdot{3}+{1}={17}$$$, $$${p}'{\left({2}\right)}={3}\cdot{{2}}^{{2}}+{6}\cdot{2}-{2}={22}$$$, $$${p}''{\left({2}\right)}={6}\cdot{2}+{6}={18}$$$, $$${p}'''{\left({2}\right)}={6}$$$.
So,
$$${p}{\left({x}\right)}={17}+\frac{{{22}}}{{{1}!}}{\left({x}-{2}\right)}+\frac{{{18}}}{{{2}!}}{{\left({x}-{2}\right)}}^{{2}}+\frac{{{6}}}{{{3}!}}{{\left({x}-{2}\right)}}^{{3}}={17}+{22}{\left({x}-{2}\right)}+{9}{{\left({x}-{2}\right)}}^{{2}}+{{\left({x}-{2}\right)}}^{{3}}$$$.
So, equivalently polynomial $$${p}{\left({x}\right)}={{x}}^{{3}}+{3}{{x}}^{{2}}-{2}{x}+{1}$$$ can be written as $$${p}{\left({x}\right)}={{\left({x}-{2}\right)}}^{{3}}+{9}{{\left({x}-{2}\right)}}^{{2}}+{22}{\left({x}-{2}\right)}+{17}$$$.
Thus, Taylor formula for polynomials allows us to rewrite any polynomial in terms of $$${\left({x}-{a}\right)}$$$.
Now, let's see how we can use this idea for any differentiable functions.
Suppose that function $$${y}={f{{\left({x}\right)}}}$$$ has finite derivatives up to n-th order at point $$${a}$$$.
Taylor Formula for any Function. For function $$${y}={f{{\left({x}\right)}}}$$$ n-th degree Taylor polynomial at point $$${x}={a}$$$ is $$${T}_{{n}}{\left({x}\right)}={f{{\left({a}\right)}}}+\frac{{{f{'}}{\left({a}\right)}}}{{{1}!}}{\left({x}-{a}\right)}+\frac{{{f{''}}{\left({a}\right)}}}{{{2}!}}{{\left({x}-{a}\right)}}^{{2}}+\ldots+\frac{{{{f}}^{{{\left({n}-{1}\right)}}}{\left({a}\right)}}}{{{\left({n}-{1}\right)}!}}{{\left({x}-{a}\right)}}^{{{n}-{1}}}+\frac{{{{f}}^{{{\left({n}\right)}}}{\left({a}\right)}}}{{{n}!}}{{\left({x}-{a}\right)}}^{{n}}$$$.
Of course, $$${T}_{{n}}{\left({x}\right)}\ne{f{{\left({x}\right)}}}$$$, but as appeared $$${T}_{{n}}{\left({x}\right)}$$$ is a very good approximation for $$${f{{\left({x}\right)}}}$$$ when $$${x}\to{a}$$$. And the higher $$${n}$$$ (order of polynomial) the better approximation.
Fact. $$${T}_{{n}}{\left({x}\right)}\approx{f{{\left({x}\right)}}}$$$ as $$${x}\to{a}$$$.
This fact allows us to approximate function by polynomial near point $$${x}={a}$$$ with any precision we want, by taking high degree polynomial.
Example 2. Find first, third and fifth degree polynomials for function $$${f{{\left({x}\right)}}}={\sin{{\left({x}\right)}}}$$$ near 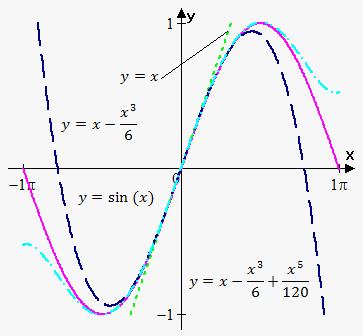 $$${x}={0}$$$.
$$${x}={0}$$$.
Here $$${a}={0}$$$.
To find fifth degree polynomial we need derivatives up to fifth order.
We have that $$${f{'}}{\left({x}\right)}={\cos{{\left({x}\right)}}}$$$, $$${f{''}}{\left({x}\right)}=-{\sin{{\left({x}\right)}}}$$$, $$${f{'''}}{\left({x}\right)}=-{\cos{{\left({x}\right)}}}$$$, $$${{f}}^{{{\left({4}\right)}}}{\left({x}\right)}={\sin{{\left({x}\right)}}}$$$, $$${{f}}^{{{\left({5}\right)}}}{\left({x}\right)}={\cos{{\left({x}\right)}}}.$$$
Now, $$${f{{\left({0}\right)}}}={0}$$$, $$${f{'}}{\left({0}\right)}={1}$$$, $$${f{''}}{\left({0}\right)}={0}$$$, $$${f{'''}}{\left({0}\right)}=-{1}$$$, $$${{f}}^{{{\left({4}\right)}}}{\left({0}\right)}={0}$$$, $$${{f}}^{{{\left({5}\right)}}}{\left({0}\right)}={1}$$$.
First degree taylor polynomial is $$${T}_{{1}}{\left({x}\right)}={f{{\left({0}\right)}}}+\frac{{{f{'}}{\left({0}\right)}}}{{{1}!}}{\left({x}-{0}\right)}={0}+\frac{{1}}{{1}}{x}={x}$$$.
Third degree taylor polynomial is $$${T}_{{3}}{\left({x}\right)}={f{{\left({0}\right)}}}+\frac{{{f{'}}{\left({0}\right)}}}{{{1}!}}{\left({x}-{0}\right)}+\frac{{{f{''}}{\left({0}\right)}}}{{{2}!}}{{\left({x}-{0}\right)}}^{{2}}+\frac{{{f{'''}}{\left({0}\right)}}}{{{3}!}}{{\left({x}-{0}\right)}}^{{3}}={0}+\frac{{1}}{{1}}{x}+\frac{{0}}{{{2}}}{{x}}^{{2}}+\frac{{-{1}}}{{{6}}}{{x}}^{{3}}={x}-\frac{{{{x}}^{{3}}}}{{6}}$$$.
Fifth degree taylor polynomial is $$${T}_{{5}}{\left({x}\right)}={f{{\left({0}\right)}}}+\frac{{{f{'}}{\left({0}\right)}}}{{{1}!}}{\left({x}-{0}\right)}+\frac{{{f{''}}{\left({0}\right)}}}{{{2}!}}{{\left({x}-{0}\right)}}^{{2}}+\frac{{{f{'''}}{\left({0}\right)}}}{{{3}!}}{{\left({x}-{0}\right)}}^{{3}}+\frac{{{{f}}^{{{\left({4}\right)}}}{\left({0}\right)}}}{{{4}!}}{{\left({x}-{0}\right)}}^{{4}}+\frac{{{{f}}^{{{\left({5}\right)}}}{\left({0}\right)}}}{{{5}!}}{{\left({x}-{0}\right)}}^{{5}}=$$$
$$$={0}+\frac{{1}}{{1}}{x}+\frac{{0}}{{{2}}}{{x}}^{{2}}+\frac{{-{1}}}{{{6}}}{{x}}^{{3}}+\frac{{0}}{{{4}!}}{{x}}^{{4}}+\frac{{1}}{{{120}}}{{x}}^{{5}}={x}-\frac{{{{x}}^{{3}}}}{{6}}+\frac{{{{x}}^{{5}}}}{{{120}}}$$$.
So,
$$${T}_{{1}}{\left({x}\right)}={x}$$$, $$${T}_{{3}}{\left({x}\right)}={x}-\frac{{{{x}}^{{3}}}}{{6}}$$$, $$${T}_{{5}}{\left({x}\right)}={x}-\frac{{{{x}}^{{3}}}}{{6}}+\frac{{{{x}}^{{5}}}}{{120}}$$$.
Remember, the higher degree of polynomial, the better precision. Figure illustrates this. Note, that approximation good only near point of expansion, in this case $$${a}={0}$$$.
