Tangent Line in Polar Coordinates
Let's see how to derive equation of tangent line when we are given equation of curve $$${r}={f{{\left(\theta\right)}}}$$$ in polar coordinates.
We will proceed in the same fashion as with tangent lines to parametric curves, because polar coordinates in some sense similar to parametric curves.
We know that $$${x}={r}{\cos{{\left(\theta\right)}}}$$$ and $$${y}={r}{\sin{{\left(\theta\right)}}}$$$.
Since we are given that $$${r}={f{{\left(\theta\right)}}}$$$ we should treat $$${r}$$$ as a function of $$$\theta$$$.
To find slope of tangent line, we need to find $$$\frac{{{d}{y}}}{{{d}{x}}}$$$ but in terms of $$${r}$$$ and $$$\theta$$$. This can be easily done with chain rule:
$$$\frac{{{d}{y}}}{{{d}{x}}}=\frac{{{d}{y}}}{{{d}\theta}}\cdot\frac{{{d}\theta}}{{{d}{x}}}=\frac{{{d}{y}}}{{{d}\theta}}\cdot\frac{{1}}{{\frac{{{d}{x}}}{{{d}\theta}}}}$$$.
We have that $$$\frac{{{d}{y}}}{{{d}\theta}}=\frac{{{d}{r}}}{{{d}\theta}}{\sin{{\left(\theta\right)}}}+{r}{\cos{{\left(\theta\right)}}}$$$ and $$$\frac{{{d}{x}}}{{{d}\theta}}=\frac{{{d}{r}}}{{{d}\theta}}{\cos{{\left(\theta\right)}}}-{r}{\sin{{\left(\theta\right)}}}$$$.
So, we obtained following fact.
Fact. Slope of tangent line in polar coordinates is $$$\frac{{{d}{y}}}{{{d}{x}}}=\frac{{\frac{{{d}{r}}}{{{d}\theta}}{\sin{{\left(\theta\right)}}}+{r}{\cos{{\left(\theta\right)}}}}}{{\frac{{{d}{r}}}{{{d}\theta}}{\cos{{\left(\theta\right)}}}-{r}{\sin{{\left(\theta\right)}}}}}$$$.
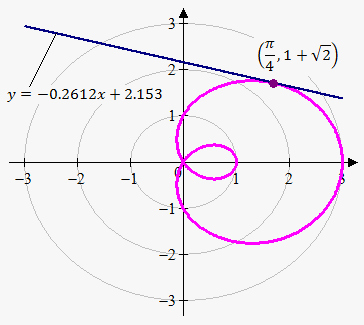
Example. Find equation of tangent line to $$${r}={1}+{2}{\cos{{\left(\theta\right)}}}$$$ at $$$\theta=\frac{\pi}{{4}}$$$.
 We have that $$$\frac{{{d}{r}}}{{{d}\theta}}=-{2}{\sin{{\left(\theta\right)}}}$$$, so
We have that $$$\frac{{{d}{r}}}{{{d}\theta}}=-{2}{\sin{{\left(\theta\right)}}}$$$, so
$$$\frac{{{d}{y}}}{{{d}{x}}}=\frac{{-{2}{\sin{{\left(\theta\right)}}}{\sin{{\left(\theta\right)}}}+{\left({1}+{2}{\cos{{\left(\theta\right)}}}\right)}{\cos{{\left(\theta\right)}}}}}{{-{2}{\sin{{\left(\theta\right)}}}{\cos{{\left(\theta\right)}}}-{\left({1}+{2}{\cos{{\left(\theta\right)}}}\right)}{\sin{{\left(\theta\right)}}}}}=$$$
$$$=\frac{{{\cos{{\left(\theta\right)}}}+{2}{\cos{{\left({2}\theta\right)}}}}}{{-{\sin{{\left(\theta\right)}}}-{2}{\sin{{\left({2}\theta\right)}}}}}$$$.
So, slope of tangent line at point $$$\theta=\frac{\pi}{{4}}$$$ is $$${m}=\frac{{{d}{y}}}{{{d}{x}}}{\mid}_{{\theta=\frac{\pi}{{4}}}}=\frac{{{\cos{{\left(\frac{\pi}{{4}}\right)}}}+{2}{\cos{{\left(\frac{\pi}{{2}}\right)}}}}}{{-{\sin{{\left(\frac{\pi}{{4}}\right)}}}-{2}{\sin{{\left(\frac{\pi}{{2}}\right)}}}}}=\frac{{1}}{{7}}{\left({1}-{2}\sqrt{{{2}}}\right)}$$$.
Now we need corresponding $$${x}$$$ and $$${y}$$$ coordinates when $$$\theta=\frac{\pi}{{4}}$$$:
$$${x}={r}{\cos{{\left(\theta\right)}}}={\left({1}+{2}{\cos{{\left(\theta\right)}}}\right)}{\cos{{\left(\theta\right)}}}={\left({1}+{2}{\cos{{\left(\frac{\pi}{{4}}\right)}}}\right)}{\cos{{\left(\frac{\pi}{{4}}\right)}}}=\frac{{{1}+\sqrt{{{2}}}}}{\sqrt{{{2}}}}$$$.
$$${y}={r}{\sin{{\left(\theta\right)}}}={\left({1}+{2}{\cos{{\left(\theta\right)}}}\right)}{\sin{{\left(\theta\right)}}}={\left({1}+{2}{\cos{{\left(\frac{\pi}{{4}}\right)}}}\right)}{\sin{{\left(\frac{\pi}{{4}}\right)}}}=\frac{{{1}+\sqrt{{{2}}}}}{\sqrt{{{2}}}}$$$.
So, equation of tangent line that passes through point $$$\theta=\frac{\pi}{{4}}$$$ is $$${y}=\frac{{1}}{{7}}{\left({1}-{2}\sqrt{{{2}}}\right)}{\left({x}-\frac{{{1}+\sqrt{{{2}}}}}{\sqrt{{{2}}}}\right)}+\frac{{{1}+\sqrt{{{2}}}}}{\sqrt{{{2}}}}$$$ or approximately $$${y}=-{0.2612}{x}+{2.153}$$$.
As with parametric curves there are curves that have several tangent line at one point. For example, in above example, such point is (0,0). The corresponding value(s) of $$$\theta$$$ we can find by solving equation $$${1}+{2}{\cos{{\left(\theta\right)}}}={0}$$$. This gives two solutions on interval $$${\left[{0},{2}\pi\right]}$$$: $$$\frac{{{2}\pi}}{{3}}$$$ and $$$\frac{{{4}\pi}}{{3}}$$$, so there will be two tangent lines at (0,0).
Similarly to parametric curves, curve in polar coordinates has
- horizontal tangent when $$$\frac{{{d}{y}}}{{{d}\theta}}={0}$$$ (provided that $$$\frac{{{d}{x}}}{{{d}\theta}}\ne{0}$$$).
- vertical tangent when $$$\frac{{{d}{x}}}{{{d}\theta}}={0}$$$ (provided that $$$\frac{{{d}{y}}}{{{d}\theta}}\ne{0}$$$).
