What is Irrational Number

Irrational number is a number, that is not rational.

What does that mean?

It means, that we can't represent irrational number as a fraction, decimal with finite number of digits, or repeating decimal.

For, example:

Whole number 3 can be represented as $\frac{{3}}{{1}}$ .
Fraction $\frac{{5}}{{10}}$ is already fraction (reduced form is $\frac{{1}}{{2}}$ ).
Decimal ${0.16}$ is $\frac{{4}}{{25}}$ .
Repeating decimal ${0.33333333}={0}.{\overline{{{3}}}}$ is $\frac{{1}}{{3}}$ .

Irrational numbers often occur, when we want to find nth root of a number.

For example, ${\sqrt[{{3}}]{{{7}}}}$ is irrational, because there is no such fraction $\frac{{m}}{{n}}$ , that ${{\left(\frac{{m}}{{n}}\right)}}^{{3}}={7}$ .

A couple of famous irrational numbers are: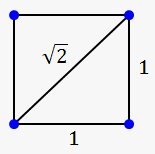 square root of 2

$\pi\approx{3.1415926535898}$ (ratio of circumference of any circle and its diameter)
$\sqrt{{{2}}}\approx{1.4142135623731}$ (length of diagonal of the square with sides equal 1)

As can be seen, irrational numbers can be represented as decimals, but what then is the difference between repeating decimal and irrational number?

Answer is simple. Irrational number has no pattern in decimal representation.

Compare:

$\frac{{10}}{{11}}={0.909090909090}\ldots.={0}.{\overline{{{90}}}}$ (here is pattern, we know what comes next: 90)
$\pi={3.1415926535897}\ldots$ (what's next???)

Maybe, you don't believe that $\sqrt{{{2}}}$ is irrational, so here is proof.

Fact. $\sqrt{{{2}}}$ is irrational.

Proof. Pretend that we can represent $\sqrt{{{2}}}$ as irreducible fraction $\frac{{m}}{{n}}$ , that is $\sqrt{{{2}}}=\frac{{m}}{{n}}$ .

If numbers are equal, then their squares are also equal: ${{\left(\sqrt{{{2}}}\right)}}^{{2}}={{\left(\frac{{m}}{{n}}\right)}}^{{2}}$ .

This can be rewritten as ${2}=\frac{{{m}}^{{2}}}{{{n}}^{{2}}}$ .

From last equality we have that ${{m}}^{{2}}={2}{{n}}^{{2}}$ .

This means, that ${{m}}^{{2}}$ is even. But if ${{m}}^{{2}}$ is even, then ${m}$ is also even (square of odd number will give odd number).

That's why we can write ${m}$ as ${m}={2}{c}$ .

Return to ${{m}}^{{2}}={2}{{n}}^{{2}}$ and plug instead of ${m}$ ${2}{c}$ : ${{\left({2}{c}\right)}}^{{2}}={2}{{n}}^{{2}}$ .

This means that ${4}{{c}}^{{2}}={2}{{n}}^{{2}}$ or ${2}{{c}}^{{2}}={{n}}^{{2}}$ .

So, ${n}$ is also even number.

Since ${n}$ is even and ${m}$ is even, then $\frac{{m}}{{n}}$ is not irreducible (they have at least one common factor 2).

This is contradiction.

So, there is no such fraction $\frac{{m}}{{n}}$ , that $\sqrt{{{2}}}=\frac{{m}}{{n}}$ .

Thus, $\sqrt{{{2}}}$ is irrational.

When does irrational number occur?

Some known constants: $\pi$ , ${e}$ (Euler number) etc.
Nth root of numbers: $\sqrt{{{2}}},{\sqrt[{{3}}]{{{2}}}}$ etc.

But keep in mind, that not all nth roots are irrational. For example $\sqrt{{{4}}}={2}$ , ${\sqrt[{{4}}]{{{81}}}}={3}$ .

Finally, multiplication of irrational numbers can give rational number:

$\sqrt{{{3}}}\cdot\sqrt{{{3}}}={{\left(\sqrt{{{3}}}\right)}}^{{2}}={3}$
$\sqrt{{{2}}}\cdot\sqrt{{{8}}}={4}$

But that's not always true: ${\pi}^{{2}}=\pi\cdot\pi={9.869604401}$ is still irrational.