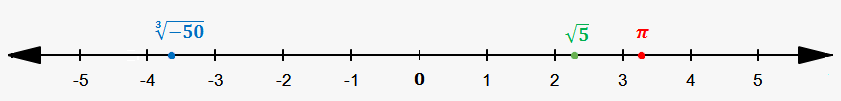Irrational Numbers on a Number Line

Since each irrational number can be represented as infinite decimal, then we can proceed in the same way, as we did when placed decimals on a number line.

$\pi\approx{3.14}$, so it is slightly to the right of 3.

Since ${4}<{5}<{9}$, then $\sqrt{{{4}}}<\sqrt{{{5}}}<\sqrt{{{9}}}$ or ${2}<\sqrt{{{5}}}<{3}$. So, $\sqrt{{{5}}}$ is somewhere between 2 and 3 (close to 2, because $\sqrt{{{5}}}\approx{2.236}$).

Similarly, since $-{64}<-{50}<-{27}$, then ${\sqrt[{{3}}]{{-{64}}}}<{\sqrt[{{3}}]{{-{50}}}}<{\sqrt[{{3}}]{{-{27}}}}$ or $-{4}<\sqrt{{-{50}}}<-{3}$. So, ${\sqrt[{{3}}]{{-{50}}}}$ is somewhere between -4 and -3 (closer to -4, because ${\sqrt[{{3}}]{{-{50}}}}\approx-{3.684}$).