Definition of the Limit of a Function
We've already talked about the limit of a sequence, and, since a sequence is a particular case of a function, there will be a similarity between the sequence and the function. We are also going to extend some concepts.
Example 1. Let's investigate the behavior of $$${y}={{x}}^{{2}}$$$ near the point $$${x}={2}$$$.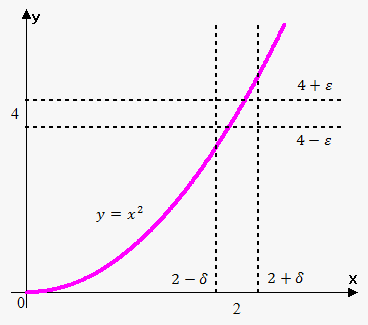
To do this, let's take the points sufficiently close to $$$2$$$ and evaluate the corresponding y-values.
| $$${x}$$$ | 1.9 | 1.99 | 1.999 | 2.0001 | 2.001 | 2.01 |
| $$${y}={{x}}^{{2}}$$$ | 3.61 | 3.9601 | 3.996001 | 4.00040001 | 4.004001 | 4.0401 |
We see that as $$${x}$$$ approaches $$$2$$$, $$${f{{\left({x}\right)}}}$$$ approaches $$$4$$$, no matter whether we take the points greater than $$$2$$$ or less than $$$2$$$. We write this fact as $$$\lim_{{{x}\to{2}}}{{x}}^{{2}}={4}$$$.
Definition. We write that $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={L}$$$ and say, "the limit of $$$f(x)$$$, as $$$x$$$ approaches $$$a$$$, equals $$$L$$$" if for any $$$\epsilon>{0}$$$ there exists $$$\delta>{0}$$$ such that $$${\left|{f{{\left({x}\right)}}}-{L}\right|}<\epsilon$$$ when $$${\left|{x}-{a}\right|}<\delta$$$.
To put it simply, this means that $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={L}$$$ if we can make $$${f{{\left({x}\right)}}}$$$ as close to $$${L}$$$ as we like by taking an $$${x}$$$ sufficiently close to $$${a}$$$.
We will also use the following notation: $$${f{{\left({x}\right)}}}\to{L}$$$ as $$${x}\to{a}$$$.
From the definition, it follows that we only care about the behavior of the function at the points near $$${a}$$$, not at $$${a}$$$ itself. This means that $$${f{{\left({x}\right)}}}$$$ can even be not defined at $$${a}$$$ but still have $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}$$$.
For example, consider the function $$${f{{\left({x}\right)}}}={{x}}^{{2}}$$$ and $$${g{{\left({x}\right)}}}={\left\{\begin{array}{c}{{x}}^{{2}}{\quad\text{if}\quad}{x}\ne{2}\\\text{undefined}{\quad\text{if}\quad}{x}={2}\\ \end{array}\right.}$$$.
Note that $$$\lim_{{{x}\to{2}}}{f{{\left({x}\right)}}}=\lim_{{{x}\to{2}}}{g{{\left({x}\right)}}}={4}$$$ even despite the fact that $$${g{{\left({x}\right)}}}$$$ is not defined at $$$2$$$. That's because we don't care about the function at $$$2$$$, we are only interested in the bevavior near $$$2$$$.
Note that $$${\left|{x}-{a}\right|}<\delta$$$ is equivalent to the double inequality $$$-\delta<{x}-{a}<\delta$$$ or $$${a}-\delta<{x}<{a}+\delta$$$.
Let's do a couple of examples trying to guess the limit. Note that this approach is not correct but it allows to understand better the limits.
Example 2. Calculate $$$\lim_{{{x}\to{1}}}{\left({x}+{1}\right)}$$$.
Let's see what value $$${\left({x}+{1}\right)}$$$ approaches as $$${x}$$$ approaches $$$1$$$.
| $$$x$$$ | 0.9 | 0.99 | 0.999 | 1.0001 | 1.001 | 1.01 |
| $$${y}={x}+{1}$$$ | 1.9 | 1.99 | 1.999 | 2.0001 | 2.001 | 2.01 |
So, as $$${x}$$$ approaches $$$1$$$, $$${f{{\left({x}\right)}}}$$$ approaches $$$2$$$; thus, $$$\lim_{{{x}\to{1}}}{\left({x}+{1}\right)}={2}$$$.
One more quick example.
Example 3. Calculate $$$\lim_{{{x}\to{1}}}\frac{{{x}-{1}}}{{{{x}}^{{2}}-{1}}}$$$.
Let's see what value $$$\frac{{{x}-{1}}}{{{{x}}^{{2}}-{1}}}$$$ approaches when $$${x}$$$ approaches $$$1$$$.
| $$$x$$$ | 0.9 | 0.99 | 0.999 | 1.0001 | 1.001 | 1.01 |
| $$${y}=\frac{{{x}-{1}}}{{{{x}}^{{2}}-{1}}}$$$ | $$$\frac{{{0.9}-{1}}}{{{{0.9}}^{{2}}-{1}}}={0.5263}$$$ | 0.5025 | 0.5003 | 0.499975 | 0.49975 | 0.4975 |
So, as $$$x$$$ approaches $$$1$$$, $$${f{{\left({x}\right)}}}$$$ approaches $$$0.5$$$; thus, $$$\lim_{{{x}\to{1}}}\frac{{{x}-{1}}}{{{{x}}^{{2}}-{1}}}=\frac{{1}}{{2}}$$$.
And another useful example.
Example 4. Calculate $$$\lim_{{{x}\to{0}}}{\cos{{\left(\frac{\pi}{{x}}\right)}}}$$$.
Let's see where $$${\cos{{\left(\frac{\pi}{{x}}\right)}}}$$$ goes when $$${x}$$$ approaches $$$0$$$.
| $$${x}$$$ | $$${f{{\left({x}\right)}}}$$$ |
| 1 | $$${\cos{{\left(\frac{\pi}{{1}}\right)}}}=-{1}$$$ |
| 0.1 | $$${\sin{{\left(\frac{\pi}{{0.1}}\right)}}}=-{1}$$$ |
| 0.001 | $$${\sin{{\left(\frac{\pi}{{0.001}}\right)}}}=-{1}$$$ |
| 0.0001 | $$${\sin{{\left(\frac{\pi}{{0.0001}}\right)}}}=-{1}$$$ |
It seems that $$$\lim_{{{x}\to{0}}}{\cos{{\left(\frac{\pi}{{x}}\right)}}}=-{1}$$$, but this is the WRONG answer! The reason is that we took only the values at which $$${\cos{{\left(\frac{\pi}{{x}}\right)}}}=-{1}$$$.
Note that $$${\cos{{\left(\frac{\pi}{{x}}\right)}}}=-{1}$$$ when $$${x}=\frac{{1}}{{n}}$$$ for any integer $$${n}$$$.
But also $$${\cos{{\left(\frac{\pi}{{x}}\right)}}}={0}$$$ for infinitely many values of $$${x}$$$ that approach $$$0$$$. In fact, as $$${x}$$$ approaches $$$0$$$, the cosine takes any value from the interval $$${\left[-{1},{1}\right]}$$$. In other words, $$${\cos{{\left(\frac{\pi}{{x}}\right)}}}$$$ oscillates infinitely many times as $$${x}$$$ approaches $$$0$$$.
Since $$${\cos{{\left(\frac{\pi}{{x}}\right)}}}$$$ doesn't approach any fixed value, $$$\lim_{{{x}\to{0}}}{\cos{{\left(\frac{\pi}{{x}}\right)}}}$$$ doesn't exist.
This example shows that we can guess the wrong value if we take the inappropriate values of $$${x}$$$. It is also difficult to understand when to stop calculating the values. However, we will give the correct methods for calculating the limits.
Let's finalize our work with one last example.
Example 5. Calculate $$$\lim_{{{x}\to{0}}}\frac{{1}}{{{x}}^{{2}}}$$$.
As $$$x$$$ approaches $$$0$$$, $$${{x}}^{{2}}$$$ also approaches $$$0$$$; so, $$$\frac{{1}}{{{x}}^{{2}}}$$$ becomes very large (for example, when $$${x}={0.001}$$$, we have that $$$\frac{{1}}{{{x}}^{{2}}}={1000000}$$$). Thus, the value of $$${f{{\left({x}\right)}}}$$$ approaches infinity without a bound; so, $$$\lim_{{{x}\to{0}}}\frac{{1}}{{{x}}^{{2}}}=\infty$$$.
