Limit of a Sequence

Often we are interested in value that sequence will take as number ${n}$ becomes very large.

Definition. Constant number ${a}$ is called a limit of the sequence ${x}_{{n}}$ if for every $\epsilon>{0}$ there exists number ${N}$ , such that all values ${x}_{{n}}$ whose number ${n}>{N}$ , satisfy inequality ${\left|{x}_{{n}}-{a}\right|}<\epsilon$ .

The fact that ${a}$ is a limit of sequence is written as $\lim{x}_{{n}}={a}$ or $\lim{x}={a}$ or $\lim_{{{n}\to\infty}}{x}_{{n}}={a}$ .

Also we say that variable approaches ${a}$ : ${x}_{{n}}\to{a}$ or ${x}\to{a}$ .

This definition can be reformulated in simple words: ${a}$ is a limit of the sequence if diffrerence between its values and ${a}$ becomes very small $\left({\left|{x}_{{n}}\right|}-{a}<\epsilon\right)$ , starting with some number ${N}$ .

Definition. Sequence is called convergent (converges to ${a}$ ) if there exists such finite number ${a}$ that $\lim_{{{n}\to\infty}}{x}_{{n}}={a}$ . Otherwise, sequence diverges or divergent.

In other words sequence is convergent if it approaches some finite number.

Note, that symbol $\infty$ means infinity (very large number). So, if sequence has limit ${a}$ then members in this sequence starting with some number ${N}$ approach ${a}$ .

For example, sequence ${x}_{{n}}=\frac{{1}}{{n}}$ and corresponding list ${\left\{{1},\frac{{1}}{{2}},\frac{{1}}{{3}},\frac{{1}}{{4}},\frac{{1}}{{5}},\ldots\right\}}$ approach 0 because ${x}_{{{10000}}}=\frac{{1}}{{{10000}}}$ and ${x}_{{{100000}}}=\frac{{1}}{{{100000}}}$ ; we see that the greater ${n}$ , the closer value to 0.

It is important to notice, that number ${N}$ depends on the choice of $\epsilon$ . Therefore, we will write sometimes ${N}_{{\epsilon}}$ instead of ${N}$ . In general the lesser $\epsilon$ , the greater ${N}$ : if we require more closeness, the more bigger values of sequence we need to consider. The only exception is when all values in sequence are same and equal ${a}$ . In this case ${a}=\lim{x}_{{n}}$ , and inequality will hold for any $\epsilon$ for all ${x}_{{n}}$ (same can be said if values of sequence equal a, starting from some number).

By the property of absolute values ${\left|{x}_{{n}}-{a}\right|}<\epsilon$ is equivalent to $-\epsilon<{x}_{{n}}-{a}<\epsilon$

or ${a}-\epsilon<{x}_{{n}}<{a}+\epsilon$ .

Therefore, we have geometric interpretation of limit. If we take any segment of length ${2}\epsilon$ with center a, then all points ${x}_{{n}}$ starting with some number should lie within this segment (only finite number of points can lie outside the interval).

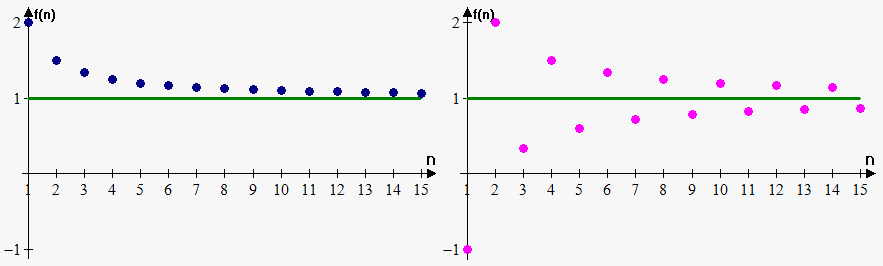
Also sequences can approach same value but approach it in different manner.

Consider two sequences: ${x}_{{n}}={1}-\frac{{1}}{{n}}$ (corresponding list of members is ${\left\{{0},\frac{{1}}{{2}},\frac{{2}}{{3}},\frac{{3}}{{4}},\frac{{4}}{{5}},\ldots\right\}}$ )and ${y}_{{n}}={1}+{2}\frac{{{{\left(-{1}\right)}}^{{n}}}}{{n}}$ (corresponding list of members is ${\left\{-{1},{2},\frac{{1}}{{3}},\frac{{3}}{{2}},\ldots\right\}}$ ).

See how, closer becomes point to line ${y}={1}$ when n becomes larger. Thus, it is natural to suggest that both sequences have limit 1. But they approach it differently: if we on x-axis set natural numbers and on y-axis values that sequence will take then we will obtain following graph (see figure below). But we are not interested how sequence behaves from the "start", we are interested how it behaves when ${n}$ becomes very large.

different approach to the limit

Example 1. Show that limit of ${x}_{{n}}=\frac{{1}}{{n}}+{1}$ equals 1.

To prove this by definition we need for every $\epsilon>{0}$ find such natural number ${N}$ that for every ${n}>{N}$ ${\left|{x}_{{n}}-{1}\right|}<\epsilon$ .

So, ${\left|{x}_{{n}}-{1}\right|}={\left|\frac{{1}}{{n}}+{1}-{1}\right|}={\left|\frac{{1}}{{n}}\right|}$ .

Thus, ${\left|\frac{{1}}{{n}}\right|}<\epsilon$ when ${n}>\frac{{1}}{\epsilon}$ . Therefore, we can take ${N}_{\epsilon}={\left[\frac{{1}}{\epsilon}\right]}$ , where ${\left[{x}\right]}$ is a floor function.

If we take $\epsilon={0.01}$ then ${N}_{\epsilon}={\left[\frac{{1}}{{0.01}}\right]}={100}$ . So, members starting with 101-th number will be different from 1 on less than $\epsilon$ : Indeed, ${x}_{{{101}}}=\frac{{1}}{{101}}+{1}={1.0099}$ and ${\left|{1.0099}-{1}\right|}<{0.01}$ .

If we take $\epsilon={0.5}$ then ${N}_{\epsilon}={\left[\frac{{1}}{{0.5}}\right]}={2}$ . So, members starting with 3-rd number will be different from 1 on less than $\epsilon$ : Indeed, ${x}_{{{3}}}=\frac{{1}}{{3}}+{1}=\frac{{4}}{{3}}\approx{1.3333}$ and ${\left|{1.3333}-{1}\right|}<{0.5}$ .

As can be seen for different $\epsilon$ there are different values of ${N}_{\epsilon}$ . Limit exists when for any $\epsilon$ we can find corresponding ${N}_{\epsilon}$ .

Therefore, $\lim_{{{n}\to\infty}}{x}_{{n}}=\lim_{{{n}\to\infty}}{\left({1}+\frac{{1}}{{n}}\right)}={1}$ .

Example 2. Show that sequence ${x}_{{n}}={{\left(-{1}\right)}}^{{n}}$ doesn't have limit.

This sequence is represented by list ${\left\{-{1},{1},-{1},{1},-{1},{1},\ldots\right\}}$ .

If we take $\epsilon={0.01}$ then we can't find ${N}$ such that for ${n}>{N}$ members will be close to some number (limit), because members oscillate: sequence takes by turn values 1 or -1. Thus, this sequence doesn't have a limit.

Following fact closes this note.

Fact. A sequence can't have more than one limit.

This means that sequence either doesn't have limit or has exactly one limit.