Absolute Value

Absolute value makes any number positive.

On a number line we saw positive (to the right of zero) and negative (to the left of zero) numbers. There direction matters.

Absolute value doesn't care about direction. It only shows how far from zero number is.

Notation for absolute value: $$$\color{red}{\left|a\right|}$$$.

Keep in mind that absolute value is denoted by vertical bars, not square brackets or something else.

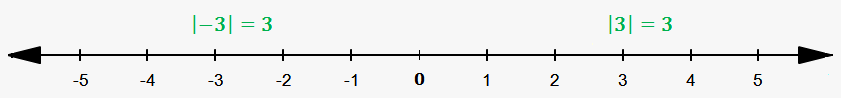
Let's do a couple of examples.

Example 1. $$${\left|{5}\right|}={5}$$$ (already positive number, so absolute value does nothing).

Example 2. $$${\left|-{10}\right|}={10}$$$ (negative number becomes positive).

Be careful with minus sign.

Example 3. $$$-{\left|{7}\right|}=-{7}$$$ (absolute value contains positive number, minus is outside).

Example 4. $$$-{\left|-{18}\right|}=-{18}$$$ (absolute value "eats" inner minus, but doesn't influence outer one).

Example 5. $$$-{\left|{5}-{7}\right|}=-{\left|-{2}\right|}=-{2}$$$ (we can perform operations inside absolute value as well).

Try to solve a couple of problems.