Differentials
Suppose that we are given a function $$$y={f{{\left({x}\right)}}}$$$. Consider the interval $$${\left[{a},{a}+\Delta{x}\right]}$$$. The corresponding change in $$${y}$$$ is $$$\Delta{y}={f{{\left({a}+\Delta{x}\right)}}}-{f{{\left({a}\right)}}}$$$.
We are interested in the following question: is there a constant $$$C$$$ such that $$$\Delta{y}\approx{C}\Delta{x}$$$ when $$$\Delta{x}\to{0}$$$?
Let's go through a couple of examples.
Example 1. The area of a circle with the radius $$$r$$$ is $$$A=\pi{{r}}^{{2}}$$$.
If we increase $$$r$$$ by $$$\Delta{r}$$$, then the corresponding increase in $$${A}$$$ is $$$\Delta{A}=\pi{{\left({r}+\Delta{r}\right)}}^{{2}}-\pi{{r}}^{{2}}={2}\pi{r}\Delta{r}+{{\left(\Delta{r}\right)}}^{{2}}$$$.
When $$$\Delta{r}\to{0}$$$, we have that $$${{\left(\Delta{r}\right)}}^{{2}}$$$ becomes very small, so we can write that $$$\Delta{A}\approx{2}\pi{r}\Delta{r}$$$.
Let's move on.
Example 2. The volume of a sphere with the radius $$${r}$$$ is $$${V}=\frac{{4}}{{3}}\pi{{r}}^{{3}}$$$.
If we increase $$${r}$$$ by $$$\Delta{r}$$$, then the corresponding increase in $$${V}$$$ is $$$\Delta{V}=\frac{{4}}{{3}}\pi{{\left({r}+\Delta{r}\right)}}^{{3}}-\frac{{4}}{{3}}\pi{{r}}^{{3}}={4}\pi{{r}}^{{2}}\Delta{r}+{4}\pi{r}{{\left(\Delta{r}\right)}}^{{2}}+\frac{{4}}{{3}}\pi{{\left(\Delta{r}\right)}}^{{3}}$$$.
When $$$\Delta{r}\to{0}$$$, we have that both $$${{\left(\Delta{r}\right)}}^{{2}}$$$ and $$${{\left(\Delta{r}\right)}}^{{3}}$$$ become very small, so we can write that $$$\Delta{V}\approx{4}\pi{{r}}^{{2}}\Delta{r}$$$.
In the above examples, we can see the same thing.
In Example 1, when $$${A}=\pi{{r}}^{{2}}$$$, we have that $$$\Delta{A}\approx{2}\pi{r}\Delta{r}$$$, but $$${2}\pi{r}$$$ is the derivative of $$$\pi{{r}}^{{2}}$$$ with respect to $$${r}$$$.
In Example 2, when $$${V}=\frac{{4}}{{3}}\pi{{r}}^{{3}}$$$, we have that $$$\Delta{V}\approx{4}\pi{{r}}^{{2}}\Delta{r}$$$, but again, $$${4}\pi{{r}}^{{2}}$$$ is the derivative of $$$\frac{{4}}{{3}}\pi{{r}}^{{3}}$$$ with respect to $$${r}$$$.
In fact, this is true for any function in general.
Definition. A function $$${y}={f{{\left({x}\right)}}}$$$ is called differentiable at the point $$${a}$$$ if and only if it has a finite derivative $$${f{'}}{\left({a}\right)}$$$.
Fact. If the function $$${y}={f{{\left({x}\right)}}}$$$ is differentiable, then $$$\Delta{y}\approx{f{'}}{\left({x}\right)}\Delta{x}$$$, or $$${d}{y}\approx\Delta{y}$$$. The expression $$${f{'}}{\left({x}\right)}\Delta{x}$$$ is called the differential of the function $$${f{{\left({x}\right)}}}$$$ and is denoted by $$${d}{y}$$$. So, $$${d}{y}={f{'}}{\left({x}\right)}\Delta{x}$$$.
The differential of the independent variable $$${x}$$$ is just its increase, i.e. $$${d}{x}=\Delta{x}$$$.
Thus, the differential of the function can be rewritten as $$${d}{y}={f{'}}{\left({x}\right)}{d}{x}$$$, or $$${f{'}}{\left({x}\right)}=\frac{{{d}{y}}}{{{d}{x}}}$$$.
We can now treat $$$\frac{{{d}{y}}}{{{d}{x}}}$$$ as a ratio, not just as a symbol.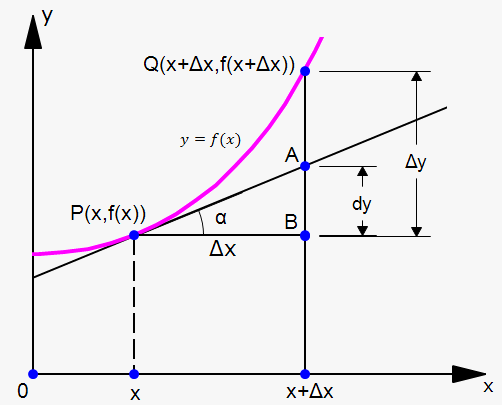
Now, let's see the geometric meaning of the differential.
Let $$${P}={\left({x},{f{{\left({x}\right)}}}\right)}$$$ and $$${Q}={\left({x}+\Delta{x},{f{{\left({x}+\Delta{x}\right)}}}\right)}$$$ be points on the graph $$${f{}}$$$ and let $$$\Delta{x}={d}{x}$$$. The corresponding change in $$${y}$$$ is $$$\Delta{y}={f{{\left({x}+\Delta{x}\right)}}}-{f{{\left({x}\right)}}}$$$.
The slope of the tangent line $$${P}{A}$$$ is the derivative $$${f{'}}{\left({x}\right)}$$$. Thus, the directed distance from $$$A$$$ to $$$B$$$ is $$${f{'}}{\left({x}\right)}{d}{x}={d}{y}$$$. Therefore, $$${d}{y}$$$ represents the amount by which the tangent line rises or falls (the change in linearization), whereas $$$\Delta{y}$$$ represents the amount by which the curve $$${y}={f{{\left({x}\right)}}}$$$ rises or falls when $$${x}$$$ changes by the amount $$${d}{x}$$$. Notice that the approximation $$$\Delta{y}\approx{d}{y}$$$ becomes better as $$$\Delta{x}$$$ becomes smaller.
Since $$$\Delta{y}={f{{\left({a}+\Delta{x}\right)}}}-{f{{\left({a}\right)}}}$$$, we can write that $$${f{{\left({a}+{d}{x}\right)}}}-{f{{\left({a}\right)}}}\approx{d}{y}$$$.
This can be rewritten as $$${f{{\left({a}+{d}{x}\right)}}}\approx{f{{\left({a}\right)}}}+{d}{y}$$$.
This formula is used for approximating the values of functions.
Example 3. Approximate the value of $$$\sqrt{{{16.05}}}$$$ using the function $$${f{{\left({x}\right)}}}=\sqrt{{{x}+{4}}}$$$.
$$${d}{y}={f{'}}{\left({x}\right)}{d}{x}=\frac{{1}}{{{2}\sqrt{{{x}+{4}}}}}{d}{x}$$$
If $$${a}={12}$$$ and $$${d}{x}=\Delta{x}={0.05}$$$, then
$$${d}{y}=\frac{{1}}{{{2}\sqrt{{{12}+{4}}}}}{0.05}={0.00625}$$$.
Now, $$$\sqrt{{{16.05}}}={f{{\left({12.05}\right)}}}={f{{\left({12}+{0.05}\right)}}}\approx{f{{\left({12}\right)}}}+{d}{y}={4}+{0.00625}={4.00625}$$$.
