Theorems involving Continuous Functions

Intermediate Value Theorem. Suppose that $f$ is continuous on closed interval ${\left[{a},{b}\right]}$ and let ${N}$ is any number between ${f{{\left({a}\right)}}}$ and ${f{{\left({b}\right)}}}$ (or ${f{{\left({b}\right)}}}$ and ${f{{\left({a}\right)}}}$ ; depends what is bigger). Then there exists number ${c}$ in ${\left({a},{b}\right)}$ such that ${f{{\left({c}\right)}}}={N}$ .

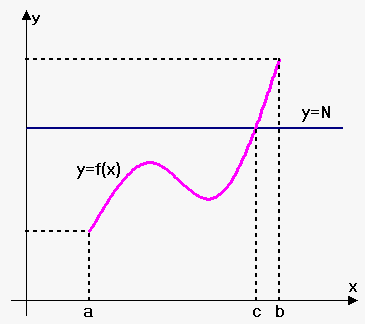The Intermediate Value Theorem states that a continuous function takes on every intermediate value between the function values ${f{{\left({a}\right)}}}$ and ${f{{\left({b}\right)}}}$ .

Note that the value ${N}$ can be taken one or more times.

In geometric terms Intermediate Value Theorem states that if any horizontal line ${y}=$ is given between ${f{{\left({a}\right)}}}$ and ${f{{\left({b}\right)}}}$ then the graph of ${f{}}$ should intersect ${y}={N}$ somewhere.

Corollary. Suppose that ${f{}}$ is continuous on closed interval ${\left[{a},{b}\right]}$ such that ${f{{\left({a}\right)}}}$ and ${f{{\left({b}\right)}}}$ have different signs. Then there exists number ${c}$ in ${\left({a},{b}\right)}$ such that ${f{{\left({c}\right)}}}={0}$ .

Proof of this fact is straightforward. Since ${f{{\left({a}\right)}}}$ and ${f{{\left({b}\right)}}}$ have different signs then either ${f{{\left({a}\right)}}}<{0}<{f{{\left({b}\right)}}}$ or ${f{{\left({b}\right)}}}<{0}<{f{{\left({a}\right)}}}$ , so, we take ${N}={0}$ in intermediate value theorem.

Note, that Intermediate Value Theorem is general false for discontinuous functions.

One use of the Intermediate Value Theorem is in locating roots of equations.

Example 1. Function ${{2}}^{{x}}-{4}{x}={0}$ clearly has root 4, but it is harder to locate another root. However, for function ${f{{\left({x}\right)}}}={{2}}^{{x}}-{4}{x}$ ${f{{\left({0}\right)}}}={{2}}^{{0}}-{4}\cdot{0}={1}>{0}$ and ${f{{\left(\frac{{1}}{{2}}\right)}}}={{2}}^{{\frac{{1}}{{2}}}}-{4}\cdot{2}=\sqrt{{{2}}}-{8}<{0}$ .

Thus, by corollary (because function ${f{{\left({x}\right)}}}={{2}}^{{x}}-{4}{x}$ is continuous) there exists number ${c}$ in interval ${\left({0},\frac{{1}}{{2}}\right)}$ such that ${f{{\left({c}\right)}}}={0}$ .

Example 2. Show that the root of equation ${\cos{{\left({x}\right)}}}-{x}={0}$ is within interval [0,1].

Let ${f{{\left({x}\right)}}}={\cos{{\left({x}\right)}}}-{x}$ . Clearly it is continuous on [0,1].

We are looking for the solution of the equation, that is a number ${c}$ between 0 and 1 such that ${f{{\left({c}\right)}}}={0}$ .

Since ${f{{\left({0}\right)}}}={\cos{{\left({0}\right)}}}-{0}={1}>{0}$ and ${f{{\left({1}\right)}}}={\cos{{\left({1}\right)}}}-{1}<{0}$ then ${f{{\left({1}\right)}}}<{0}<{f{{\left({0}\right)}}}$ .

Thus, according to corollary there exists number ${c}$ on interval ${\left({0},{1}\right)}$ such that ${f{{\left({c}\right)}}}={0}$ . Therefore, ${f{{\left({x}\right)}}}$ has at least one root in (0,1).

Boundedness of a function. Suppose that function ${f{}}$ is continuous on closed interval ${\left[{a},{b}\right]}$ then exist such constant finite numbers ${m}$ and ${M}$ that ${m}\le{f{{\left({x}\right)}}}\le{M}$ for all ${a}\le{x}\le{b}$ .

Note that this theorem doesn't hold if interval is not closed.

For example, let ${f{{\left({x}\right)}}}={\left\{\begin{array}{c}\frac{{1}}{{x}}{\quad\text{if}\quad}{0}<{x}\le{1}\\{0}{\quad\text{if}\quad}{x}={0}\\ \end{array}\right.}$ .

This function can take only finite values, but it grows without a bound when ${x}$ approaches 0.