One-Sided Continuity. Classification of Discontinuities

Similarly to the one-sided limits, we can define one-sided continuity.

Definition. Function ${f{{\left({x}\right)}}}$ is continuous from the right at point ${a}$ if $\lim_{{{x}\to{{a}}^{+}}}={f{{\left({a}\right)}}}$ . Function ${f{{\left({x}\right)}}}$ is continuous from the left at point ${a}$ if $\lim_{{{x}\to{{a}}^{{-}}}}{f{{\left({x}\right)}}}={f{{\left({a}\right)}}}$ .

Clearly, if function is continuous from the left and from the right at point ${a}$ , then it is continuous at point ${a}$ .

Definition. Function ${f{}}$ is discontinuous at ${a}$ if it is not continuous.

There are three kinds of discontinuity at ${a}$ :

Removable Discontinuity: if $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}$ exists and finite, but function is either undefined at point ${a}$ or $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}\ne{f{{\left({a}\right)}}}$ . It is called removable because this discontinuity can be removed by redefining function as ${g{{\left({x}\right)}}}={\left\{\begin{array}{c}{f{{\left({x}\right)}}}{\quad\text{if}\quad}{x}\ne{a}\\\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}{\quad\text{if}\quad}{x}={a}\\ \end{array}\right.}$
Jump or Step Discontinuity: if one-sided limits exist and finite but not equal.
Infinite or Essential Discontinuity: if one or both of the one-sided limits don't exist or are infinite.

Let's go through a couple of examples of these discontinuities.

Example 1. Find where function ${f{{\left({x}\right)}}}=\frac{{{{x}}^{{2}}+{2}{x}-{3}}}{{{x}-{1}}}$ is discontinuous and classify this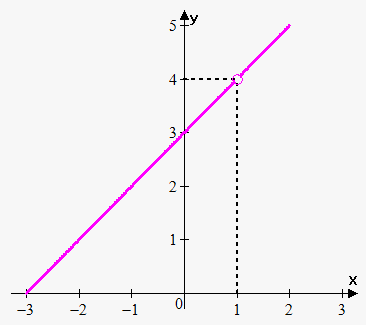 removable discontinuity and function is not defined discontinuity.

This function is rational, so it is continuous everywhere, except where denominator equals 0, i.e. where ${x}-{1}={0}$ . So, functions is not defined (and not continuous) when ${x}={1}$ .

Now, $\lim_{{{x}\to{1}}}\frac{{{{x}}^{{2}}+{2}{x}-{3}}}{{{x}-{1}}}=\lim_{{{x}\to{1}}}\frac{{{\left({x}+{3}\right)}{\left({x}-{1}\right)}}}{{{x}-{1}}}=$

$=\lim_{{{x}\to{1}}}{\left({x}+{3}\right)}={4}$ .

Thus, limit exists and finite, but ${f{{\left({1}\right)}}}$ is not defined, so ${x}={1}$ is removable discontinuity.

Example 2. Find where function ${f{{\left({x}\right)}}}={\left\{\begin{array}{c}\frac{{{{x}}^{{2}}+{2}{x}-{3}}}{{{x}-{1}}}{\quad\text{if}\quad}{x}\ne{1}\\{2}{\quad\text{if}\quad}{x}={1}\\ \end{array}\right.}$ is discontinuous and classify this discontinuity.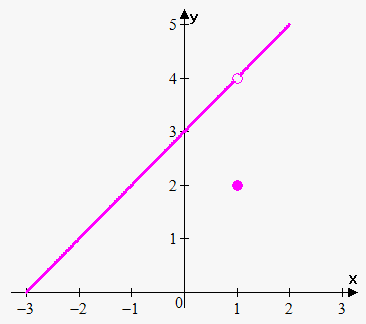 removable discontinuity and function is defined

This is actually same example as example 1, except that function is defined at ${x}={1}$ .

Again $\lim_{{{x}\to{1}}}\frac{{{{x}}^{{2}}+{2}{x}-{3}}}{{{x}-{1}}}={4}$ , but ${f{{\left({1}\right)}}}={2}$ , so $\lim_{{{x}\to{1}}}\frac{{{{x}}^{{2}}+{2}{x}-{3}}}{{{x}-{1}}}\ne{f{{\left({1}\right)}}}$ .

Thus, ${x}={1}$ is point of removable discontinuity.

As in example 1 we can make function continuous by redefining function as ${f{{\left({x}\right)}}}={\left\{\begin{array}{c}\frac{{{{x}}^{{2}}+{2}{x}-{3}}}{{{x}-{1}}}{\quad\text{if}\quad}{x}\ne{1}\\{4}{\quad\text{if}\quad}{x}={1}\\ \end{array}\right.}$ .

Example 3. Find where function ${f{{\left({x}\right)}}}={\left\{\begin{array}{c}{x}+{1}{\quad\text{if}\quad}{x}\le{2}\\{4}-{x}{\quad\text{if}\quad}{x}>{2}\\ \end{array}\right.}$ is discontinuous and classify 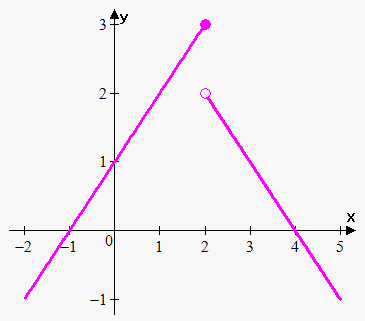jump discontinuity this discontinuity.

Clearly linear functions are continuous everywhere, but since $\lim_{{{x}\to{{2}}^{{-}}}}{f{{\left({x}\right)}}}=\lim_{{{x}\to{{2}}^{{-}}}}{\left({x}+{1}\right)}={3}$ and $\lim_{{{x}\to{{2}}^{+}}}{f{{\left({x}\right)}}}=\lim_{{{x}\to{{2}}^{+}}}{\left({4}-{x}\right)}={2}$ then $\lim_{{{x}\to{{2}}^{{-}}}}{f{{\left({x}\right)}}}\ne\lim_{{{x}\to{{2}}^{+}}}{f{{\left({x}\right)}}}$ .

This means that at ${x}={2}$ there is jump discontinuity.

Also note, that $\lim_{{{x}\to{{2}}^{{-}}}}{f{{\left({x}\right)}}}={3}={f{{\left({1}\right)}}}$ , this means that function is continuous from the left at ${x}={2}$ .

Example 4. Find where function ${f{{\left({x}\right)}}}=\frac{{1}}{{{x}-{1}}}$ is discontinuous and classify this discontinuity. infinite discontinuity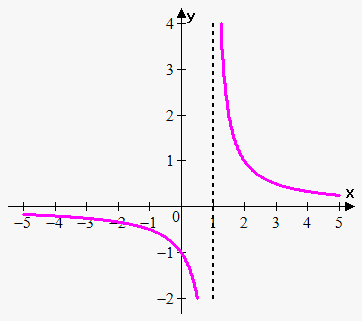

This function is rational, so it is continuous everywhere, except where denominator equals 0, i.e. where ${x}-{1}={0}.$ So, functions is not continuous when ${x}={1}$ .

Now, $\lim_{{{x}\to{{1}}^{+}}}\frac{{1}}{{{x}-{1}}}=\infty$ .

This means that at ${x}={1}$ there is infinite discontinuity.

Actually infinite discontinuity occurs when we have vertical asymptote.

Example 5. Find points where function ${f{}}$ is discontinuous and classify these points: 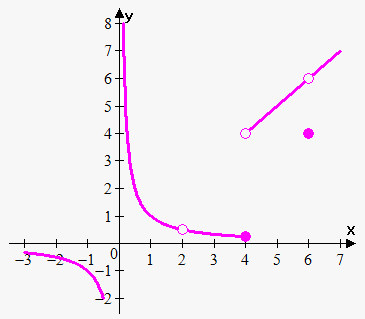all types of discontinuities ${f{{\left({x}\right)}}}={\left\{\begin{array}{c}\frac{{1}}{{x}}{\quad\text{if}\quad}{x}<{2}\\\frac{{1}}{{x}}{\quad\text{if}\quad}{2}<{x}\le{4}\\{x}{\quad\text{if}\quad}{4}<{x}<{6}\\{4}{\quad\text{if}\quad}{x}={6}\\{x}{\quad\text{if}\quad}{x}>{6}\\ \end{array}\right.}$

Function is discontinuous at 0 because $\lim_{{{x}\to{{0}}^{+}}}{f{{\left({x}\right)}}}=\lim_{{{x}\to{{0}}^{+}}}\frac{{1}}{{x}}=\infty$ . So, at function ${x}={0}$ we have infinite discontinuity.

Function is dicontinuous at 2 because ${f{{\left({2}\right)}}}$ is simply not defined. Since $\lim_{{{x}\to{{2}}^{{-}}}}\frac{{1}}{{x}}=\lim_{{{x}\to{{2}}^{+}}}\frac{{1}}{{x}}=\frac{{1}}{{2}}$ then $\lim_{{{x}\to{2}}}\frac{{1}}{{x}}=\frac{{1}}{{2}}$ and so ${x}={2}$ is removable discontinuity.

Since $\lim_{{{x}\to{{4}}^{{-}}}}{f{{\left({x}\right)}}}=\lim_{{{x}\to{{4}}^{{-}}}}\frac{{1}}{{x}}=\frac{{1}}{{4}}$ and $\lim_{{{x}\to{{4}}^{+}}}{f{{\left({x}\right)}}}=\lim_{{{x}\to{{4}}^{+}}}{x}={4}$ then $\lim_{{{x}\to{4}}}{f{{\left({x}\right)}}}$ doesn't exist because one-sided limits are not equal.

This means that ${x}={4}$ is jump discontinuity.

Since $\lim_{{{x}\to{{6}}^{{-}}}}{f{{\left({x}\right)}}}=\lim_{{{x}\to{{6}}^{{-}}}}{x}={6}$ and $\lim_{{{x}\to{{6}}^{+}}}{f{{\left({x}\right)}}}=\lim_{{{x}\to{{6}}^{+}}}{x}={6}$ then $\lim_{{{x}\to{6}}}{f{{\left({x}\right)}}}={6}$ but ${f{{\left({6}\right)}}}={4}\ne{6}$ , so $\lim_{{{x}\to{6}}}{f{{\left({x}\right)}}}\ne{f{{\left({6}\right)}}}$ .

This means that ${x}={6}$ is removable discontinuity.

Example 6. Conside function ${f{{\left({x}\right)}}}={\left[{x}\right]}$ where ${\left[{x}\right]}$ is a floor function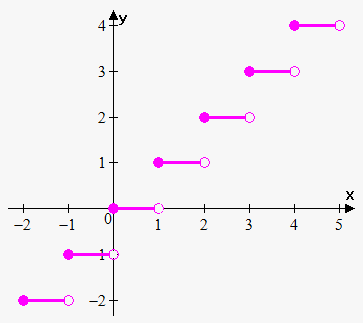 infinite number of jump discontinuities .

This function is discontinuous at every integer point ${x}={n}$ , because $\lim_{{{x}\to{{n}}^{{-}}}}{\left[{x}\right]}={n}-{1}$ and $\lim_{{{x}\to{{n}}^{+}}}{\left[{x}\right]}={n}$ .

So one-sided limits are finite but not equal. This means that at every integer point ${x}={n}$ there is jump discontinuity.

Also, note that ${f{{\left({n}\right)}}}={n}=\lim_{{{x}\to{{n}}^{+}}}{f{{\left({x}\right)}}}$ that's why at every integer point ${x}={n}$ function is continuous from the right.