Logarithmic Functions

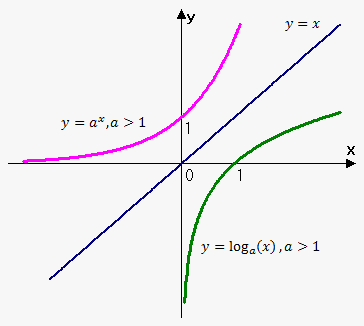logarithmic function Since exponential function ${y}={{a}}^{{x}}$ is monotonic (i.e. either increasing or decreasing) then it passes horizontal line test. Thus, it has inverse function. To find this function we use algorithm for finding inverse.

Interchange ${x}$ and ${y}$ : ${x}={{a}}^{{y}}$ . To write this in terms of ${y}$ we introduce new record: ${y}={\log}_{{a}}{\left({x}\right)}$ .

So, ${x}={{a}}^{{y}}$ is equivalent to ${y}={\log}_{{a}}{\left({x}\right)}$ . For example, ${\log}_{{2}}{\left({8}\right)}={3}$ because ${{2}}^{{3}}={8}$ .

Function ${y}={\log}_{{a}}{\left({x}\right)}$ is called logarithmic function. Its domain is ${\left({0},\infty\right)}$ and range is ${\left(-\infty,\infty\right)}$ .

Since ${y}={\log}_{{a}}{\left({x}\right)}$ is inverse of ${y}={{a}}^{{x}}$ then their graphs are symmetric about line ${y}={x}$ .

Properties of Logarithms

If ${x}$ and ${y}$ are positive numbers then

${{a}}^{{{\log}_{{a}}{\left({x}\right)}}}={x}$ , for any ${x}$ ,
${\log}_{{a}}{\left({{a}}^{{x}}\right)}={x}$ , for ${x}>{0}$ ,
${\log}_{{a}}{\left({x}{y}\right)}={\log}_{{a}}{\left({x}\right)}+{\log}_{{a}}{\left({y}\right)}$ ,
${\log}_{{a}}{\left(\frac{{x}}{{y}}\right)}={\log}_{{a}}{\left({x}\right)}-{\log}_{{a}}{\left({y}\right)}$ ,
${\log}_{{a}}{\left({{x}}^{{b}}\right)}={b}{\log}_{{a}}{\left({x}\right)}$ (where ${b}$ is any real number)

First two properties follow from definition of inverse, last three properties follow from corresponding properties of exponentials.

Example 1. Evaluate ${\log}_{{2}}{\left({3}\right)}+{\log}_{{2}}{\left({20}\right)}-{\log}_{{2}}{\left({15}\right)}$ .

Using properties of logarithms we can write that ${\log}_{{2}}{\left({3}\right)}+{\log}_{{2}}{\left({20}\right)}-{\log}_{{2}}{\left({15}\right)}={\log}_{{2}}{\left({3}\cdot{20}\right)}-{\log}_{{2}}{\left({15}\right)}={\log}_{{2}}{\left({60}\right)}-{\log}_{{2}}{\left({15}\right)}={\log}_{{2}}{\left(\frac{{60}}{{15}}\right)}={\log}_{{2}}{\left({4}\right)}={2}$

because ${{2}}^{{2}}={4}$ .

Natural logarithm

Of all possible bases ${a}$ the most convenient when working with logarithms is base ${e}$ (number ${e}\approx{2.718}$ ). We will talk why is this so in next notes.

So, logarithm with base ${e}$ is called natural logarithm and is denoted as ${\ln{{\left({x}\right)}}}$ : ${\log}_{{e}}{\left({x}\right)}={\ln{{\left({x}\right)}}}$ .

From definition of inverse it follows that ${\ln{{\left({x}\right)}}}={y}\ \Leftrightarrow\ {{e}}^{{y}}={x}$ .

Also, ${\ln{{\left({{e}}^{{x}}\right)}}}={x}$ for ${x}\in{\left(-\infty,\ \infty\right)}$ and ${{e}}^{{{\ln{{\left({x}\right)}}}}}={x}$ for ${x}>{0}$ .

In particular ${\ln{{\left({e}\right)}}}={1}$ .

Example 2. Solve equation ${{e}}^{{{3}{x}+{5}}}={4}$ .

Take natural logaritms of both sides: ${\ln{{\left({{e}}^{{{3}{x}+{5}}}\right)}}}={\ln{{\left({4}\right)}}}$ or ${3}{x}+{5}={\ln{{\left({4}\right)}}}$ , so ${x}=\frac{{{\ln{{\left({4}\right)}}}-{5}}}{{3}}$ .

Example 3. Solve ${\ln{{\left({{x}}^{{3}}+{1}\right)}}}={2}$ .

Apply exponential function to both sides of equation: ${{e}}^{{{\ln{{\left({{x}}^{{3}}+{1}\right)}}}}}={{e}}^{{2}}$ or ${{x}}^{{3}}+{1}={{e}}^{{2}}$ .

So, ${x}={\sqrt[{{3}}]{{{{e}}^{{2}}-{1}}}}$ .

Example 4. Simplify ${2}{\ln{{\left({x}\right)}}}-\frac{{1}}{{3}}{\ln{{\left({y}\right)}}}$ .

Using properties of logarithms we can write that ${2}{\ln{{\left({x}\right)}}}-\frac{{1}}{{3}}{\ln{{\left({y}\right)}}}={\ln{{\left({{x}}^{{2}}\right)}}}-{\ln{{\left({{y}}^{{\frac{{1}}{{3}}}}\right)}}}={\ln{{\left(\frac{{{{x}}^{{2}}}}{{{{y}}^{{\frac{{1}}{{3}}}}}}\right)}}}$ .

Now, let's see how can we express logaritm with one base through logarithm with another base.

Let ${y}={\log}_{{a}}{\left({x}\right)}$ . This means that ${{a}}^{{y}}={x}$ .

Taking logarithms with base ${b}$ we have that ${\log}_{{b}}{\left({{a}}^{{y}}\right)}={\log}_{{b}}{\left({x}\right)}$ or ${y}{\log}_{{b}}{\left({a}\right)}={\log}_{{b}}{\left({x}\right)}$ .

Thus, ${y}=\frac{{{\log}_{{b}}{\left({x}\right)}}}{{{\log}_{{b}}{\left({a}\right)}}}$ . From another side ${y}={\log}_{{a}}{\left({x}\right)}$ .

Finally, ${\log}_{{a}}{\left({x}\right)}=\frac{{1}}{{{\log}_{{b}}{\left({a}\right)}}}{\log}_{{b}}{\left({x}\right)}$ .

Change of base formula. ${\log}_{{a}}{\left({x}\right)}=\frac{{{\log}_{{b}}{\left({x}\right)}}}{{{\log}_{{b}}{\left({a}\right)}}}$ .

In case when ${b}={e}$ we can write equation as ${\color{blue}{{{\log}_{{a}}{\left({x}\right)}=\frac{{\ln{{\left({x}\right)}}}}{{\ln{{\left({a}\right)}}}}}}}$ .