Exponential Function

A function of the form ${f{{\left({x}\right)}}}={{a}}^{{x}}$ , where ${a}>{0}$ , is called an exponential function.

Do not confuse it with the power function ${f{{\left({x}\right)}}}={{x}}^{{a}}$ in which the variable is the base.

The domain of the exponential function is ${\left(-\infty,\infty\right)}$ , and the range is ${\left({0},\infty\right)}$ , provided ${a}\ne{1}$ .

If ${a}={1}$ , we have that ${f{{\left({x}\right)}}}={{1}}^{{x}}={1}$ .

Exponential functions are useful for modeling many natural phenomena such as population growth (if ${a}>{1}$ ) and radioactive decay (if ${0}<{a}<{1}$ ).

Let's see what is meant under ${f{{\left({x}\right)}}}={{a}}^{{x}}$ .

If ${x}={n}$ , where ${n}$ is a postive integer, we have that ${{a}}^{{n}}=\underbrace{\left({a}\cdot{a}\cdot\ldots\cdot{a}\right)}_{{{n}}}$ .

If ${x}={0}$ , it can be stated that ${{a}}^{{0}}={1}$ , and if ${x}=-{n}$ , where ${n}$ is a positive integer, we have that ${{a}}^{{-{n}}}=\frac{{1}}{{{{a}}^{{n}}}}$ .

If ${x}$ is a rational number, ${x}=\frac{{p}}{{q}}$ , where ${p}$ and ${q}$ are integers, it can be stated that ${{a}}^{{x}}={{a}}^{{\frac{{p}}{{q}}}}={\sqrt[{{q}}]{{{{a}}^{{p}}}}}={{\left({\sqrt[{{q}}]{{a}}}\right)}}^{{p}}$ .

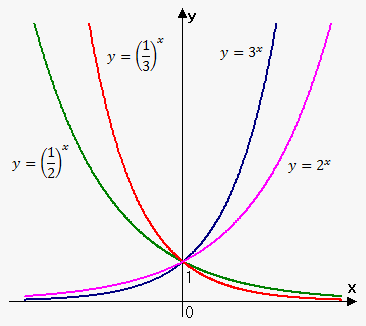
There are three kinds of exponential functions:

If ${0}<{a}<{1}$ , the exponential function decreases.
If ${a}={1}$ , the exponential function is constant.
If ${a}>{1}$ , it increases (the bigger ${a}$ , the more rapidly it increases).

exponential function

Properties of exponents.

If ${a}$ and ${b}$ are positive numbers, and ${x}$ and ${y}$ are any real numbers, it can be stated that:

${{a}}^{{{x}+{y}}}={{a}}^{{x}}{{a}}^{{y}}$
${{a}}^{{{x}-{y}}}=\frac{{{{a}}^{{x}}}}{{{{a}}^{{y}}}}$
${{\left({{a}}^{{x}}\right)}}^{{{y}}}={{a}}^{{{x}{y}}}$
${{\left({a}{b}\right)}}^{{x}}={{a}}^{{x}}{{b}}^{{x}}$

Applications of exponential functions.

As stated above, exponential functions are widely used in growth/decay problems.

Example 1. Suppose that the initial population of some bacteria is 100. It is known that every 1 hour the population triples. Find the population after 10 hours.

If the number of bacteria at a time ${t}$ is ${p}{\left({t}\right)}$ , where ${t}$ is measured in hours, and ${p}{\left({0}\right)}={100}$ is the initial population, we have that

${p}{\left({1}\right)}={3}{p}{\left({0}\right)}={300}$

${p}{\left({2}\right)}={3}{p}{\left({1}\right)}={3}\cdot{3}\cdot{p}{\left({0}\right)}={{3}}^{{2}}{p}{\left({0}\right)}={900}$

${p}{\left({3}\right)}={3}{p}{\left({2}\right)}={3}\cdot{3}\cdot{3}\cdot{p}{\left({0}\right)}={{3}}^{{3}}{p}{\left({0}\right)}={2700}$

${p}{\left({4}\right)}={3}{p}{\left({3}\right)}={3}\cdot{3}\cdot{3}\cdot{3}\cdot{p}{\left({0}\right)}={{3}}^{{4}}{p}{\left({0}\right)}={8100}$ .

Do you see the pattern? It seems that ${p}{\left({t}\right)}={100}\cdot{{3}}^{{n}}$ .

So, ${p}{\left({10}\right)}={100}\cdot{{3}}^{{{10}}}={5904900}$ .

Now, let's proceed to another example.

Example 2. Suppose that the half-life of some radioactive element is 3 years (recall that the half-life is the amount of time needed to disintegrate a half of any quantity initially presented). Suppose that the initially presented mass is 1000 mg. Find the mass after 10 years.

If ${m}{\left({t}\right)}$ is the mass of the element at any time ${t}$ measured in years, we have that

${m}{\left({0}\right)}={1000}$

${m}{\left({3}\right)}=\frac{{1}}{{2}}{m}{\left({0}\right)}={500}$

${m}{\left({6}\right)}=\frac{{1}}{{2}}{m}{\left({3}\right)}=\frac{{1}}{{{2}}^{{2}}}{m}{\left({0}\right)}={250}$

From this pattern, we can conclude that

${m}{\left({t}\right)}=\frac{{1}}{{{{2}}^{{\frac{{t}}{{3}}}}}}\cdot{1000}={1000}\cdot{{2}}^{{-\frac{{t}}{{3}}}}$ .

So, in 10 years, there will be ${m}{\left({10}\right)}={1000}\cdot{{2}}^{{-\frac{{10}}{{3}}}}\approx{99.21}$ mg.