Related Rates
Suppose that we are given one quantity $$$x$$$ that depends on another quantity $$$y$$$. If the rate of change of the quantity $$$x$$$ with respect to the time $$$t$$$ is given, how do we find the rate of change of $$$y$$$ with respect to time? We need to do it because in real-world problems it is often easier to calculate the rate of change of $$$x$$$ than the rate of change of $$$y$$$.
In fact, it can be easily done using the chain rule and other differentiation rules.
Example 1. Air is being pumped into a spherical balloon so that its volume is increasing at a rate of 200 $$$\frac{{{c}{{m}}^{{3}}}}{{s}}$$$. How fast is the radius of the balloon increasing when the diameter is 60 cm?
Let $$${V}$$$ be the volume of the balloon and $$${r}$$$ be its radius; then, we need to find $$$\frac{{{d}{r}}}{{{d}{t}}}$$$ at $$${r}=\frac{{60}}{{2}}={30}$$$ given $$$\frac{{{d}{V}}}{{{d}{t}}}={200}$$$.
We know that the volume of a spherical balloon is $$${V}=\frac{{4}}{{3}}\pi{{r}}^{{3}}$$$.
Differentiating with respect to $$${t}$$$ gives (using the chain rule) $$$\frac{{{d}{V}}}{{{d}{t}}}=\frac{{{d}{V}}}{{{d}{r}}}\cdot\frac{{{d}{r}}}{{{d}{t}}}$$$.
The derivative of $$${V}$$$ with respect to $$${r}$$$ is $$$\frac{{{d}{V}}}{{{d}{r}}}={4}\pi{{r}}^{{2}}$$$.
So, $$$\frac{{{d}{V}}}{{{d}{t}}}={4}\pi{{r}}^{{2}}\frac{{{d}{r}}}{{{d}{t}}}$$$.
Plugging in the known quantities gives $$${200}={4}\pi\cdot{{30}}^{{2}}\frac{{{d}{r}}}{{{d}{t}}}$$$, or $$$\frac{{{d}{r}}}{{{d}{t}}}=\frac{{200}}{{{4}\pi\cdot{900}}}=\frac{{1}}{{{18}\pi}}$$$.
So, the radius of the balloon is increasing at a rate of $$$\frac{{1}}{{{18}\pi}}\ \frac{{{c}{m}}}{{s}}$$$.
If that is clear, let's do some more work.
Example 2. The car $$$A$$$ is traveling west at 60 $$$\frac{{{m}{i}}}{{h}}$$$, and the car $$$B$$$ is traveling north at 40 $$$\frac{{{m}{i}}}{{h}}$$$. They are both approaching the intersection of the roads. At what rate are the cars approaching each other when the car $$$A$$$ is 0.4 mi and the car $$$B$$$ is 0.3 mi from the intersection?
Let $$$C$$$ be the intersection of the roads.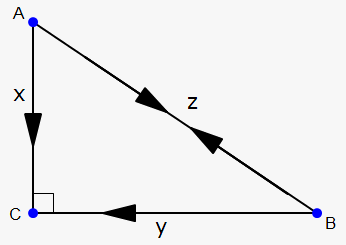
At a given time $$${t}$$$, let $$${x}$$$ be the distance from the car $$$A$$$ to $$$C$$$, $$${y}$$$ be the distance from the car $$$B$$$ to $$$C$$$, and $$${z}$$$ be the distance between the cars, where $$${x}$$$, $$${y}$$$, and $$${z}$$$ are measured in miles.
We are given that $$$\frac{{{d}{x}}}{{{d}{t}}}=-{60}$$$ and $$$\frac{{{d}{y}}}{{{d}{t}}}=-{40}$$$. (The derivatives are negative because $$${x}$$$ and $$${y}$$$ are decreasing.) We are asked to find $$$\frac{{{d}{z}}}{{{d}{t}}}$$$.
$$${x}$$$, $$${y}$$$, and $$${z}$$$ are related by the Pythagorean theorem:
$$${{z}}^{{2}}={{x}}^{{2}}+{{y}}^{{2}}$$$.
Differentiating each side with respect to $$${t}$$$, we have following:
$$${2}{z}\frac{{{d}{z}}}{{{d}{t}}}={2}{x}\frac{{{d}{x}}}{{{d}{t}}}+{2}{y}\frac{{{d}{y}}}{{{d}{t}}}$$$, or $$$\frac{{{d}{z}}}{{{d}{t}}}=\frac{{1}}{{z}}{\left({x}\frac{{{d}{x}}}{{{d}{t}}}+{y}\frac{{{d}{y}}}{{{d}{t}}}\right)}$$$.
When $$${x}={0.4}$$$ and $$${y}={0.3}$$$, the Pythagorean theorem tells that $$${z}=\sqrt{{{{x}}^{{2}}+{{y}}^{{2}}}}=\sqrt{{{{\left({0.4}\right)}}^{{2}}+{{\left({0.3}\right)}}^{{2}}}}={0.5}$$$.
Therefore, $$$\frac{{{d}{z}}}{{{d}{t}}}=\frac{{1}}{{{0.5}}}{\left({0.4}\cdot{\left(-{60}\right)}+{0.3}\cdot{\left(-{40}\right)}\right)}=-{72}$$$.
The cars are approaching each other at a rate of $$$-{72}\frac{{{m}{i}}}{{h}}$$$.
Let's move on to the next example.
Example 3. A water tank has the shape of an inverted circular cone with a base radius of 3 m and a height of 9 m. If water is being pumped into the tank at a rate of 2 $$$\frac{{{m}}^{{3}}}{\min}$$$, find the rate at which the water level is rising when the water is 4 m deep.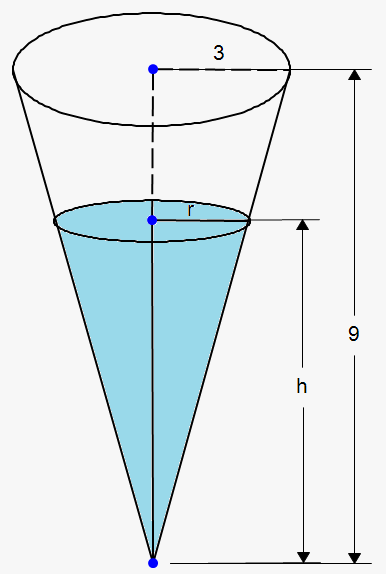
Let $$${V}$$$, $$${r}$$$, and $$${h}$$$ be the volume of the water, the radius of the surface, and the height at a time $$${t}$$$, where $$${t}$$$ is measured in minutes.
We are given that $$$\frac{{{d}{V}}}{{{d}{t}}}={2}\frac{{{m}}^{{3}}}{\min}$$$ and we are asked to find $$$\frac{{{d}{h}}}{{{d}{t}}}$$$ when $$${h}$$$ is 4 m. The quantities $$${V}$$$ and $$${h}$$$ are related by the equation $$${V}=\frac{{1}}{{3}}\pi{{r}}^{{2}}{h}$$$.
From the similarity of triangles, we make a conclusion that $$$\frac{{r}}{{3}}=\frac{{h}}{{9}}$$$, or $$${r}=\frac{{h}}{{3}}$$$.
Plugging into the equation gives $$${V}=\frac{{1}}{{3}}\pi{{\left(\frac{{h}}{{3}}\right)}}^{{2}}{h}=\frac{{1}}{{27}}\pi{{h}}^{{3}}$$$.
Now, differentiate both sides with respect to the time $$${t}$$$:
$$$\frac{{{d}{V}}}{{{d}{t}}}=\frac{{{d}{V}}}{{{d}{h}}}\frac{{{d}{h}}}{{{d}{t}}}=\frac{{1}}{{9}}\pi{{h}}^{{2}}\frac{{{d}{h}}}{{{d}{t}}}$$$, or $$$\frac{{{d}{h}}}{{{d}{t}}}=\frac{{9}}{{\pi{{h}}^{{2}}}}\frac{{{d}{V}}}{{{d}{t}}}$$$.
Substituting the given values gives $$$\frac{{{d}{h}}}{{{d}{t}}}=\frac{{9}}{{\pi\cdot{{4}}^{{2}}}}\cdot{2}=\frac{{9}}{{{8}\pi}}\approx{0.358}\frac{{m}}{\min}$$$.
That's clear. Let's do some more work.
Example 4. A man is walking along a straight path at a speed of 3 $$$\frac{{{f{{t}}}}}{{s}}$$$. A searchlight is located on the ground 20 ft from the path and is kept focused on the man. At what rate is the searchlight rotating when the man is 15 ft from the point on the path closest to the searchlight?
Let $$${x}$$$ be the distance from the man to the point on the path closest to the searchlight and $$${L}$$$ be the distance between the searchlight and the man. Let $$$\theta$$$ be the angle between the beam of the searchlight and the perpendicular to the path.
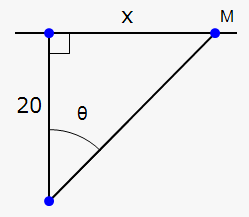
We are given that $$$\frac{{{d}{x}}}{{{d}{t}}}={3}$$$ and we need to find $$$\frac{{{d}\theta}}{{{d}{t}}}$$$ when $$${x}={15}$$$.
We need to connect $$${x}$$$ and $$$\theta$$$. This relation can be found easily. From the right-angled triangle, $$${\tan{{\left(\theta\right)}}}=\frac{{x}}{{20}}$$$.
Differentiating both sides with respect to time gives
$$${{\sec}}^{{2}}{\left(\theta\right)}\frac{{{d}\theta}}{{{d}{t}}}=\frac{{1}}{{20}}\frac{{{d}{x}}}{{{d}{t}}}$$$, or $$$\frac{{{d}\theta}}{{{d}{t}}}=\frac{{1}}{{20}}{{\cos}}^{{2}}{\left(\theta\right)}\frac{{{d}{x}}}{{{d}{t}}}$$$.
When $$${x}={15}$$$, the Pythagorean theorem tells that $$${L}=\sqrt{{{{20}}^{{2}}+{{x}}^{{2}}}}=\sqrt{{{{20}}^{{2}}+{{15}}^{{2}}}}={25}$$$.
Therefore, $$${\cos{{\left(\theta\right)}}}=\frac{{20}}{{L}}=\frac{{20}}{{25}}=\frac{{4}}{{5}}$$$.
Thus, $$$\frac{{{d}\theta}}{{{d}{t}}}=\frac{{1}}{{20}}{{\left(\frac{{4}}{{5}}\right)}}^{{2}}\cdot{3}=\frac{{12}}{{125}}={0.096}$$$.
The searchlight is rotating at a rate of $$${0.096}\frac{{{r}{a}{d}}}{{s}}$$$.
We can now proceed to the last example.
Example 5. A ladder whose length is 5 feet rests against a vertical wall. If the bottom of the ladder is sliding away from the wall at a rate of $$${2}\ \frac{{f{{t}}}}{{s}}$$$, how fast is the top of the ladder sliding down the wall when the bottom of the ladder is 4 feet from the wall?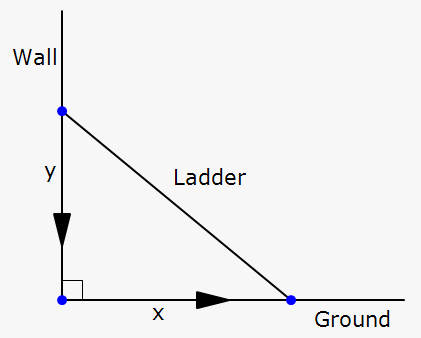
Let $$${x}$$$ feet be the distance from the bottom of the ladder to the wall and $$${y}$$$ feet be the distance from the top of the ladder to the ground.
We have that $$$\frac{{{d}{x}}}{{{d}{t}}}={2}$$$. We need to find $$$\frac{{{d}{y}}}{{{d}{t}}}$$$ when $$${x}={4}$$$.
$$${x}$$$ and $$${y}$$$ are connected by the Pythagorean theorem as follows: $$${{x}}^{{2}}+{{y}}^{{2}}={{5}}^{{2}}={25}$$$.
Differentiating this equality with respect to $$${t}$$$ gives the following:
$$${2}{x}\frac{{{d}{x}}}{{{d}{t}}}+{2}{y}\frac{{{d}{y}}}{{{d}{t}}}={0}$$$, or $$$\frac{{{d}{y}}}{{{d}{t}}}=-\frac{{x}}{{y}}\frac{{{d}{x}}}{{{d}{t}}}$$$.
From the Pythagorean theorem, when $$${x}={4}$$$, we have that $$${{y}}^{{2}}={25}-{{x}}^{{2}}={25}-{16}={9}$$$, or $$${y}={3}$$$.
So, $$$\frac{{{d}{y}}}{{{d}{t}}}=-\frac{{4}}{{3}}\cdot{2}=-\frac{{8}}{{3}}\ \frac{{f{{t}}}}{{s}}$$$.
