1. Home
  2. Math Notes
  3. Calculus II
  4. Definite Integral

Concept of Definite Integral

Related calculators: Definite and Improper Integral Calculator , Riemann Sum Calculator for a Function

In the Area Problem note, we saw that the limit of the form lim⁡n→∞f(xi⋆)Δx\lim_{{{n}\to\infty}}{f{{\left({{x}_{{i}}^{{\star}}}\right)}}}\Delta{x} arises when we compute an area.

It turns out that the same type of limit occurs in a wide variety of situations even when f{f{}} is not necessarily a positive function.

Thus, this limit has a special name and notation.

Definition of Definite Integral. If ff is a continuous function defined for a≤x≤b{a}\le{x}\le{b}, we divide the interval [a,b]{\left[{a},{b}\right]} into n{n} subintervals of equal width Δx=b−an\Delta{x}=\frac{{{b}-{a}}}{{n}}. We let x0(=a),x1,x2,…,xn(=b){x}_{{0}}{\left(={a}\right)},{x}_{{1}},{x}_{{2}},\ldots,{x}_{{n}}{\left(={b}\right)} be the endpoints of these subintervals and we choose the sample points x1⋆,x2⋆,…,xn⋆{{x}_{{1}}^{{\star}}},{{x}_{{2}}^{{\star}}},\ldots,{{x}_{{n}}^{{\star}}} in these subintervals, so that xi⋆{{x}_{{i}}^{{\star}}} lies in the ii-th subinterval [xi−1,xi]{\left[{x}_{{{i}-{1}}},{x}_{{i}}\right]}. Then, the definite integral of f{f{}} from a{a} to b{b} is ∫abf(x)dx=lim⁡n→∞∑i=1nf(xi⋆)Δx{\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}=\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{f{{\left({{x}_{{i}}^{{\star}}}\right)}}}\Delta{x}.

As with the indefinite integral, f(x){f{{\left({x}\right)}}} is called the integrand.

a{a} is the lower limit, and b{b} is the upper limit.

Note that the definite integral is a number, it doesn't depend on x{x}. We can choose another variable: ∫abf(x)dx=∫abf(t)dt=∫abf(u)du{\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}={\int_{{a}}^{{b}}}{f{{\left({t}\right)}}}{d}{t}={\int_{{a}}^{{b}}}{f{{\left({u}\right)}}}{d}{u}.

The sum ∑i=1nf(xi⋆)Δx{\sum_{{{i}={1}}}^{{n}}}{f{{\left({{x}_{{i}}^{{\star}}}\right)}}}\Delta{x} is called the Riemann sum.

If the sample points xi⋆{{x}_{{i}}^{\star}} are the left endpoints, then the sum is called the left Riemann sum; if they are the right endpoints, the sum is called the right Riemann sum.

Now, let's see what will be if f{f{}} can take both positive and negative values.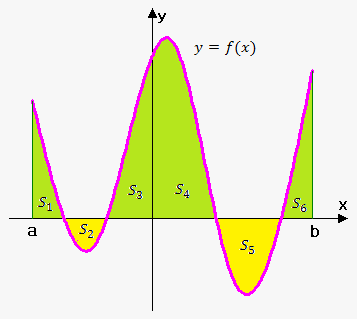net area

If f{f{}} takes on both positive and negative values, then the Riemann sum is the sum of the areas of the rectangles that lie above the x-axis minus the sum of the areas of the rectangles that lie below the x-axis.

Thus, the definite integral is the net area: the area above the x-axis minus the area below the x-axis:

∫abf(x)dx=S1−S2+S3+S4−S5+S6{\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}={S}_{{1}}-{S}_{{2}}+{S}_{{3}}+{S}_{{4}}-{S}_{{5}}+{S}_{{6}}.

Note that, although we defined ∫abf(x)dx{\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x} by dividing the interval [a,b]{\left[{a},{b}\right]} into n{n} intervals of equal width, it is sometimes advantageous to work with intervals of unequal width. If the subinterval widths are Δx1,Δx2,…,Δxn\Delta{x}_{{1}},\Delta{x}_{{2}},\ldots,\Delta{x}_{{n}} then we have to ensure that all these widths approach 00 in the limiting process. This happens if the largest width, max⁡Δxi\max\Delta{x}_{{i}}, approaches 00. So, in this case, the definition of integral becomes ∫abf(x)dx=lim⁡max⁡Δxi→0∑i=1nf(xi⋆)Δxi{\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}=\lim_{{\max\Delta{x}_{{i}}\to{0}}}{\sum_{{{i}={1}}}^{{n}}}{f{{\left({{x}_{{i}}^{{\star}}}\right)}}}\Delta{x}_{{i}}.

Now, let's go through a couple of examples.

Example 1. Express lim⁡n→∞∑i=1n[3xi2−cos⁡(xi5)]Δx\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{\left[{3}{{x}_{{i}}^{{2}}}-{\cos{{\left({{x}_{{i}}^{{5}}}\right)}}}\right]}\Delta{x} as an integral on the interval [0,π]{\left[{0},\pi\right]}.

Comparing the given limit with the limit in the definition of integral, we see that they will be identical if we choose f(x)=3x2−cos⁡(x5){f{{\left({x}\right)}}}={3}{{x}}^{{2}}-{\cos{{\left({{x}}^{{5}}\right)}}} and xi⋆=xi{{x}_{{i}}^{{\star}}}={x}_{{i}} (so that the sample points are the right endpoints). We are given that a=0{a}={0} and b=π{b}=\pi; therefore, lim⁡n→∞∑i=1n[3xi2−cos⁡(xi5)]Δx=∫0π(3x2−cos⁡(x5))dx\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{\left[{3}{{x}_{{i}}^{{2}}}-{\cos{{\left({{x}_{{i}}^{{5}}}\right)}}}\right]}\Delta{x}={\int_{{0}}^{\pi}}{\left({3}{{x}}^{{2}}-{\cos{{\left({{x}}^{{5}}\right)}}}\right)}{d}{x}.

It is very important to recognize the limits of sums as integrals. In general, if lim⁡n→∞∑i=1nf(xi⋆)Δx=∫abf(x)dx\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{f{{\left({{x}_{{i}}^{{\star}}}\right)}}}\Delta{x}={\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}, we replace lim⁡∑\lim\sum by ∫\int, xi⋆{{x}_{{i}}^{{\star}}} by x{x} and Δx\Delta{x} by dx{d}{x}.

Once it is clear, let's move on.

Example 2. Evaluate ∫02(3x2−x3)dx{\int_{{0}}^{{2}}}{\left({3}{{x}}^{{2}}-{{x}}^{{3}}\right)}{d}{x}.

Divide interval [0,2]{\left[{0},{2}\right]} into n{n} subintervals of the width Δx=2−0n=2n\Delta{x}=\frac{{{2}-{0}}}{{n}}=\frac{{2}}{{n}}.

Since we can use any point within a subinterval, let's use the right endpoints.

The right endpoint of the ii-th subinterval is 2in\frac{{{2}{i}}}{{n}}; so,

∫02(3x2−x3)dx=lim⁡n→∞∑i=1nf(in)2n=lim⁡n→∞∑i=1n(3(2in)2−(2in)3)2n=lim⁡n→∞∑i=1n(24i2n2−16i3n3)1n={\int_{{0}}^{{2}}}{\left({3}{{x}}^{{2}}-{{x}}^{{3}}\right)}{d}{x}=\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{f{{\left(\frac{{{i}}}{{n}}\right)}}}\frac{{2}}{{n}}=\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{\left({3}{{\left(\frac{{{2}{i}}}{{n}}\right)}}^{{2}}-{{\left(\frac{{{2}{i}}}{{n}}\right)}}^{{3}}\right)}\frac{{2}}{{n}}=\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{\left({24}\frac{{{i}}^{{2}}}{{{n}}^{{2}}}-{16}\frac{{{i}}^{{3}}}{{{n}}^{{3}}}\right)}\frac{{1}}{{n}}=

=lim⁡n→∞∑i=1n(24n3i2−16n4i3)=lim⁡n→∞(∑i=1n(24n3i2)−∑i=1n(16n4i3))=lim⁡n→∞(24n3∑i=1ni2−16n4∑i=1ni3)==\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{\left(\frac{{24}}{{{n}}^{{3}}}{{i}}^{{2}}-\frac{{16}}{{{n}}^{{4}}}{{i}}^{{3}}\right)}=\lim_{{{n}\to\infty}}{\left({\sum_{{{i}={1}}}^{{n}}}{\left(\frac{{24}}{{{n}}^{{3}}}{{i}}^{{2}}\right)}-{\sum_{{{i}={1}}}^{{n}}}{\left(\frac{{16}}{{{n}}^{{4}}}{{i}}^{{3}}\right)}\right)}=\lim_{{{n}\to\infty}}{\left(\frac{{24}}{{{n}}^{{3}}}{\sum_{{{i}={1}}}^{{n}}}{{i}}^{{2}}-\frac{{16}}{{{n}}^{{4}}}{\sum_{{{i}={1}}}^{{n}}}{{i}}^{{3}}\right)}=

On this stage, we need the following two formulas:

∑i=1ni2=n(n+1)(2n+1)6{\sum_{{{i}={1}}}^{{n}}}{{i}}^{{2}}=\frac{{{n}{\left({n}+{1}\right)}{\left({2}{n}+{1}\right)}}}{{6}}.

∑i=1ni3=(n(n+1)2)2{\sum_{{{i}={1}}}^{{n}}}{{i}}^{{3}}={{\left(\frac{{{n}{\left({n}+{1}\right)}}}{{2}}\right)}}^{{2}}.

So, ∫02(3x2−x3)dx=lim⁡n→∞(24n3n(n+1)(2n+1)6−16n4(n(n+1)2)2)={\int_{{0}}^{{2}}}{\left({3}{{x}}^{{2}}-{{x}}^{{3}}\right)}{d}{x}=\lim_{{{n}\to\infty}}{\left(\frac{{24}}{{{n}}^{{3}}}\frac{{{n}{\left({n}+{1}\right)}{\left({2}{n}+{1}\right)}}}{{6}}-\frac{{16}}{{{n}}^{{4}}}{{\left(\frac{{{n}{\left({n}+{1}\right)}}}{{2}}\right)}}^{{2}}\right)}=

=lim⁡n→∞(4(n+1)(2n+1)n2−4(n+1)2n2)==\lim_{{{n}\to\infty}}{\left(\frac{{{4}{\left({n}+{1}\right)}{\left({2}{n}+{1}\right)}}}{{{n}}^{{2}}}-\frac{{{4}{{\left({n}+{1}\right)}}^{{2}}}}{{{n}}^{{2}}}\right)}=

=lim⁡n→∞(4(1+1n)(2+1n)−4(1+2n+1n2))=4(1+0)(2+0)−4(1+2⋅0+0)=4=\lim_{{{n}\to\infty}}{\left({4}{\left({1}+\frac{{1}}{{n}}\right)}{\left({2}+\frac{{1}}{{n}}\right)}-{4}{\left({1}+\frac{{2}}{{n}}+\frac{{1}}{{{n}}^{{2}}}\right)}\right)}={4}{\left({1}+{0}\right)}{\left({2}+{0}\right)}-{4}{\left({1}+{2}\cdot{0}+{0}\right)}={4}

Thus, ∫02(3x2−x3)dx=4{\int_{{0}}^{{2}}}{\left({3}{{x}}^{{2}}-{{x}}^{{3}}\right)}{d}{x}={4}.

This is going to become clearer with some more practice.

Example 3. Evaluate the following integral by interpreting it in terms of areas: ∫−224−x2dx{\int_{{-{2}}}^{{2}}}\sqrt{{{4}-{{x}}^{{2}}}}{d}{x}.

Since f(x)=4−x2≥0{f{{\left({x}\right)}}}=\sqrt{{{4}-{{x}}^{{2}}}}\ge{0}, we can interpret this integral as the area under the curve y=4−x2{y}=\sqrt{{{4}-{{x}}^{{2}}}} from −2-2 to 22.

Squaring both sides gives y2=4−x2{{y}}^{{2}}={4}-{{x}}^{{2}}; then, x2+y2=4{{x}}^{{2}}+{{y}}^{{2}}={4}, and the required area is the area of the semicircle with the radius 22.

Therefore, ∫−224−x2dx=12π⋅(2)2=2π{\int_{{-{2}}}^{{2}}}\sqrt{{{4}-{{x}}^{{2}}}}{d}{x}=\frac{{1}}{{2}}\pi\cdot{{\left({2}\right)}}^{{2}}={2}\pi.

Now, let's see our final example.

Example 4. Evaluate the following integral by interpreting it in terms of areas: ∫−12(2∣x∣−1)dx{\int_{{-{{1}}}}^{{2}}}{\left({2}{\left|{x}\right|}-{1}\right)}{d}{x}.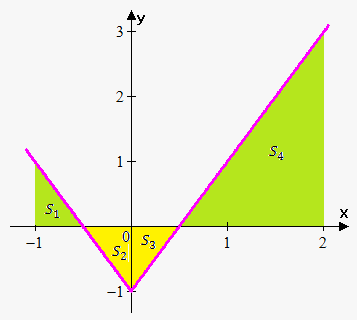example of net area

First, we draw the graph of the function y=2∣x∣−1{y}={2}{\left|{x}\right|}-{1} on the interval [−1,2]{\left[-{1},{2}\right]}.

Recall that the definite integral is the net area: ∫−12(2∣x∣−1)dx=S1−S2−S3+S4{\int_{{-{1}}}^{{2}}}{\left({2}{\left|{x}\right|}-{1}\right)}{d}{x}={S}_{{1}}-{S}_{{2}}-{S}_{{3}}+{S}_{{4}}.

Now, the area S1{S}_{{1}} is the area of a right-angled triangle with the legs 12\frac{{1}}{{2}} and 11; so, S1=12⋅12⋅1=14{S}_{{1}}=\frac{{1}}{{2}}\cdot\frac{{1}}{{2}}\cdot{1}=\frac{{1}}{{4}}.

Similarly, S2=12⋅12⋅1=14{S}_{{2}}=\frac{{1}}{{2}}\cdot\frac{{1}}{{2}}\cdot{1}=\frac{{1}}{{4}}, S3=12⋅12⋅1=14{S}_{{3}}=\frac{{1}}{{2}}\cdot\frac{{1}}{{2}}\cdot{1}=\frac{{1}}{{4}}, and S4=12⋅32⋅3=94{S}_{{4}}=\frac{{1}}{{2}}\cdot\frac{{3}}{{2}}\cdot{3}=\frac{{9}}{{4}}.

So, ∫−12(2∣x∣−1)dx=14−14−14+94=2{\int_{{-{1}}}^{{2}}}{\left({2}{\left|{x}\right|}-{1}\right)}{d}{x}=\frac{{1}}{{4}}-\frac{{1}}{{4}}-\frac{{1}}{{4}}+\frac{{9}}{{4}}={2}.