Definition of Continuous Function

Definition. A function $$$f$$$ is continuous at $$${a}$$$ if $$$\lim_{{{x}\to{a}}}={f{{\left({a}\right)}}}$$$.

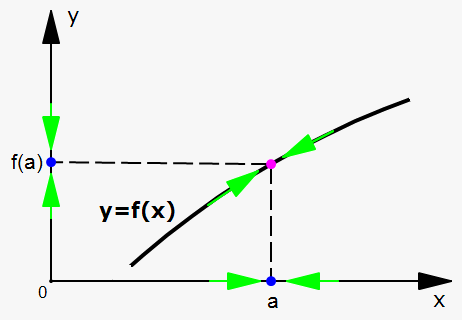continuous function Continuity implies three things:

$$${f{{\left({a}\right)}}}$$$ is defined (i.e. $$${a}$$$ is in the domain of $$${f{}}$$$);
$$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}$$$ exists;
$$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={f{{\left({a}\right)}}}$$$.

Geometrically, continuity means that you can draw a function without taking your pen off the paper.

Also, continuity means that small changes in $$${x}$$$ produce small changes in $$${y}$$$, i.e. a function is continuous at $$${a}$$$ if for any $$$\epsilon>{0}$$$ there exists $$$\delta>{0}$$$ such that $$${\left|{f{{\left({x}\right)}}}-{f{{\left({a}\right)}}}\right|}<\epsilon$$$ when $$${\left|{x}-{a}\right|}<\delta$$$.

If a function is not continuous at $$${a}$$$, we say that $$${f{}}$$$ is discontinuous at $$${a}$$$, or $$${f{}}$$$ has a discontinuity at $$${a}$$$.

Definition. The function $$${y}={f{{\left({x}\right)}}}$$$ is continuous on an interval if it is continuous at every point of the interval.

Example 1. Show that $$${f{{\left({x}\right)}}}=\sqrt{{{4}-{{x}}^{{2}}}}+{1}$$$ is continuous on the interval $$${\left(-{2},{2}\right)}$$$.

If $$$-{2}<{a}<{2}$$$, using the properties of the limits, we obtain that

$$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\lim_{{{x}\to{a}}}{\left(\sqrt{{{4}-{{x}}^{{2}}}}+{1}\right)}=$$$

$$$=\lim_{{{x}\to{a}}}\sqrt{{{4}-{{x}}^{{2}}}}+\lim_{{{x}\to{a}}}{1}=$$$ according to law 2

$$$=\sqrt{{\lim_{{{x}\to{a}}}{\left({4}-{{x}}^{{2}}\right)}}}+{1}=$$$ according to laws 7 and 8

$$$=\sqrt{{{4}-{{a}}^{{2}}}}+{1}=$$$ according to laws 2, 7, and 8

$$$={f{{\left({a}\right)}}}$$$.

Thus, $$${f{}}$$$ is continuous on $$$\left(-2, 2\right)$$$.

Actually, we can generalize the above example for any elementary function.

Continuity of Combinations of Functions. Suppose that $$${f{{\left({x}\right)}}}$$$ and $$${g{{\left({x}\right)}}}$$$ are both continuous at $$${a}$$$ and $$${c}$$$ is some arbitrary constant; then, the following functions are also continuous at $$${a}$$$:

$$${f{{\left({x}\right)}}}+{g{{\left({x}\right)}}}$$$;
$$${f{{\left({x}\right)}}}-{g{{\left({x}\right)}}}$$$;
$$${c}{f{{\left({x}\right)}}}$$$;
$$${f{{\left({x}\right)}}}{g{{\left({x}\right)}}}$$$;
$$$\frac{{{f{{\left({x}\right)}}}}}{{{g{{\left({x}\right)}}}}}$$$, if $$${g{{\left({a}\right)}}}\ne{0}$$$.

Fact. The inverse of a continuous function is also continuous.

Continuity of Elementary Functions. All elementary functions, i.e. linear, polynomial,rational, power, exponential, logarithmic, trigonometric, inverse trigonometric, hyperbolic, inverse hyperbolic, are continuous at every point of their domain.

Actually, we used this fact in previous notes. For example, since $$${y}={\cos{{\left({x}\right)}}}$$$ is continuous at $$$0$$$, we can say that $$$\lim_{{{x}\to{0}}}{\cos{{\left({x}\right)}}}={\cos{{\left({0}\right)}}}={1}$$$.

Fact. If $$${f{{\left({x}\right)}}}$$$ is continuous at $$${b}$$$ and $$$\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}={b}$$$, we have that $$$\lim_{{{x}\to{a}}}{f{{\left({g{{\left({x}\right)}}}\right)}}}={f{{\left({b}\right)}}}$$$. In other words, $$$\lim_{{{x}\to{a}}}{f{{\left({g{{\left({x}\right)}}}\right)}}}={f{{\left(\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}\right)}}}$$$.

This fact seems reasonable because if $$${x}$$$ is close to $$${a}$$$, $$${g{{\left({x}\right)}}}$$$ is close to $$${b}$$$, and, since $$${f{}}$$$ is continuous at $$${b}$$$, if $$${g{{\left({x}\right)}}}$$$ is close to $$${b}$$$, it can be stated that $$${f{{\left({g{{\left({x}\right)}}}\right)}}}$$$ is close to $$${f{{\left({b}\right)}}}$$$.

From this conclusion, we obtain the following fact:

Continuity of Composite Function. Suppose that $$${g{{\left({x}\right)}}}$$$ is continuous at $$${a}$$$ and $$${f{{\left({x}\right)}}}$$$ is continuous at $$${g{{\left({a}\right)}}}$$$; then, $$${\left({f{\circ}}{g}\right)}{\left({x}\right)}={f{{\left({g{{\left({x}\right)}}}\right)}}}$$$ is continuous at $$${a}$$$.

All the above facts allow us to easily calulate the limits of the functions that are continuous at the point $$${a}$$$.

Example 2. Find $$$\lim_{{{x}\to{1}}}\frac{{{{x}}^{{2}}+{3}{x}+{6}}}{{{2}{x}-{1}}}$$$.

Since $$${f{{\left({x}\right)}}}$$$ is a rational function, it is continuous on its domain, which in this case is $$${\left\{{x}{\mid}{x}\ne\frac{{1}}{{2}}\right\}}$$$. Thus, it is continuous at the point $$$x=1$$$.

Therefore, $$$\lim_{{{x}\to{1}}}\frac{{{{x}}^{{2}}+{3}{x}+{6}}}{{{2}{x}-{1}}}=\frac{{{{1}}^{{2}}+{3}\cdot{1}+{6}}}{{{2}\cdot{1}-{1}}}={10}$$$.

Let's work another example.

Example 3. Where is $$$\frac{{{\ln{{\left({x}\right)}}}+\sqrt{{{4}-{{x}}^{{2}}}}}}{{{{x}}^{{2}}-{1}}}$$$ continuous?

We know that $$${\ln{{\left({x}\right)}}}$$$ is continuous for $$${x}>{0}$$$ (its domain), $$$\sqrt{{{4}-{{x}}^{{2}}}}$$$ is continuous on the interval $$${\left[-{2},{2}\right]}$$$ (its domain), and the denominator is polynomial; so, it is continuous everywhere.

Thus, the function is continuous on the interval $$${\left({0},{2}\right]}$$$ where the denominator does not equal 0, or $$${x}\ne\pm{1}$$$. Therefore, the function is continuous on $$${\left({0},{1}\right)}\cup{\left({1},{2}\right]}$$$.

And one more useful example.

Example 4. Find $$$\lim_{{{x}\to\pi}}\frac{{{\cos{{\left({x}\right)}}}}}{{{1}+{\sin{{\left({x}\right)}}}}}$$$.

In the numerator, we have a continuous function $$${\cos{{\left({x}\right)}}}$$$. In the denominator, we have the sum of two continuous functions; so, the denominator is also continuous.

Thus, the ratio is continuous everywhere except where the denominator equals $$$0$$$, i.e. where $$${\sin{{\left({x}\right)}}}=-{1}$$$.

But $$${\sin{{\left(\pi\right)}}}={0}$$$; so, at this point the function is defined.

Thus, $$$\lim_{{{x}\to\pi}}\frac{{\cos{{\left({x}\right)}}}}{{{1}+{\sin{{\left({x}\right)}}}}}=\frac{{\cos{{\left(\pi\right)}}}}{{{1}+{\sin{{\left(\pi\right)}}}}}=-{1}$$$.

Memorize this and let's move on.

Example 5. Find $$$\lim_{{{x}\to{1}}}{\sin{{\left(\frac{{{{x}}^{{2}}-{1}}}{{{x}-{1}}}\right)}}}$$$.

Since the sine is a continuous function, we have that $$$\lim_{{{x}\to{1}}}{\sin{{\left(\frac{{{{x}}^{{2}}-{1}}}{{{x}-{1}}}\right)}}}={\sin{{\left(\lim_{{{x}\to{1}}}\frac{{{{x}}^{{2}}-{1}}}{{{x}-{1}}}\right)}}}=$$$

$$$={\sin{{\left(\lim_{{{x}\to{1}}}\frac{{{\left({x}-{1}\right)}{\left({x}+{1}\right)}}}{{{x}-{1}}}\right)}}}={\sin{{\left(\lim_{{{x}\to{1}}}{\left({x}+{1}\right)}\right)}}}={\sin{{\left({2}\right)}}}$$$.

Great, and now one last final example.

Example 6. Where is the function $$${h}{\left({x}\right)}={\ln{{\left(\sqrt{{{4}-{{x}}^{{2}}}}\right)}}}$$$ continuous?

Here, we have a composite function $$${h}{\left({x}\right)}={f{{\left({g{{\left({x}\right)}}}\right)}}}$$$, where $$${f{{\left({x}\right)}}}={\ln{{\left({x}\right)}}}$$$ and $$${g{{\left({x}\right)}}}=\sqrt{{{4}-{{x}}^{{2}}}}$$$.

We know that $$${\ln{{\left({x}\right)}}}$$$ is continuous for $$${x}>{0}$$$ and $$$\sqrt{{{4}-{{x}}^{{2}}}}$$$ is continuous on $$${\left[-{2},{2}\right]}$$$. Therefore, $$${h}{\left({x}\right)}$$$ is continuous on the interval $$${\left({0},{2}\right]}$$$.