Hydrostatic Pressure and Force

Suppose that a thin horizontal plate with area ${A}$ square meters is submerged in a fluid of density $\rho$ kilograms per cubic meter at a depth ${d}$ meters below the surface of the fluid.

The volume of fluid above plate is ${V}={A}{d}$, so its mass is ${m}=\rho{V}=\rho{A}{d}$.

The force exerted by the fluid on the plate is ${F}={m}{g{=}}\rho{g{{A}}}{d}$ where ${g{=}}{9.8}\frac{{m}}{{{s}}^{{2}}}$.

The pressure on the plate is defined to be the force per unit area: ${P}=\frac{{F}}{{A}}=\rho{g{{d}}}$.

The SI unit for measuring pressure is newtons per square meter, which is called a pascal $\left({1}\frac{{N}}{{{m}}^{{2}}}={1}{P}{a}\right)$. Since this is a small unit, the kilopascal (kPa) is often used.

For example, since density of water is $\rho={1000}\frac{{{k}{g}}}{{{m}}^{{3}}}$, the pressure at the bottom of a swimming pool 3 meters deep is ${P}=\rho{g{{d}}}={1000}\frac{{{k}{g}}}{{{m}}^{{3}}}\times{9.8}\frac{{m}}{{{s}}^{{2}}}\times{3}{m}={29400}{P}{a}={29.4}\ {k}{P}{a}$.

So we can determine the hydrostatic force against a vertical plate or wall or dam in a fluid. We again must use integrals, because the pressure is not constant but increases as the depth increases.

Example 1. Suppose we have a trapezoidal dam whose height is 15m. Lower base is 20 m and upper base is 30 m. Find the force on the dam due to hydrostatic pressure if the water level is 5 m from the top of the dam.

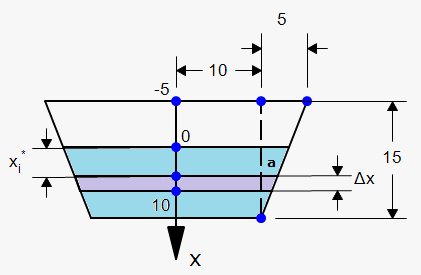
We need convention for ${x}$. Let ${x}={0}$ corresponds to the surface of water and ${x}={10}$ be bottom of the dam. Then water is in interval ${\left[{0},{10}\right]}$.

Now divide interval ${\left[{0},{10}\right]}$ into ${n}$ subintervals of equal length with endpoints ${x}_{{i}}$ and we choose ${{x}_{{i}}^{{\star}}}\in{\left[{x}_{{{i}-{1}}},{x}_{{i}}\right]}$. The i-th horizontal strip of the dam is approximated by a rectangle with height $\Delta{x}$ and width ${w}_{{i}}$,

To find ${w}_{{i}}$ we need to find ${a}$ first.

From similar triangle we have that $\frac{{a}}{{{10}-{{x}_{{i}}^{{\star}}}}}=\frac{{5}}{{15}}$ or ${a}=\frac{{10}}{{3}}-\frac{{1}}{{3}}{{x}_{{i}}^{{\star}}}$.

Therefore, ${w}_{{i}}={2}{\left({10}+{a}\right)}={2}{\left({10}+\frac{{10}}{{3}}-\frac{{1}}{{3}}{{x}_{{i}}^{{\star}}}\right)}=\frac{{80}}{{3}}-\frac{{2}}{{3}}{{x}_{{i}}^{{\star}}}$.

If ${A}_{{i}}$ is the area of the i-th strip then ${A}_{{i}}\approx{w}_{{i}}\Delta{x}={\left(\frac{{80}}{{3}}-\frac{{2}}{{3}}{{x}_{{i}}^{{\star}}}\right)}\Delta{x}$.

If $\Delta{x}$ is small then pressure ${P}_{{i}}$ is almost constant, so ${P}_{{i}}\approx\rho{{g{{x}}}_{{i}}^{{\star}}}={1000}\cdot{9.8}{{x}_{{i}}^{{\star}}}={9800}{{x}_{{i}}^{{\star}}}$.

The hydrostatic force acting on the i-th strip is the product of the pressure and the area: ${F}_{{i}}\approx{P}_{{i}}{A}_{{i}}\approx{9800}{{x}_{{i}}^{{\star}}}{\left(\frac{{80}}{{3}}-\frac{{2}}{{3}}{{x}_{{i}}^{{\star}}}\right)}\Delta{x}$.

Adding these forces and taking the limit as ${n}\to\infty$, we obtain the total hydrostatic force on the dam: ${F}=\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{9800}{{x}_{{i}}^{{\star}}}{\left(\frac{{80}}{{3}}-\frac{{2}}{{3}}{{x}_{{i}}^{{\star}}}\right)}\Delta{x}={9800}{\int_{{0}}^{{{10}}}}{x}{\left(\frac{{80}}{{3}}-\frac{{2}}{{3}}{x}\right)}{d}{x}={9800}{\int_{{0}}^{{{10}}}}{\left(\frac{{80}}{{3}}{x}-\frac{{2}}{{3}}{{x}}^{{2}}\right)}{d}{x}=$

$={9800}{\left(\frac{{40}}{{3}}{{x}}^{{2}}-\frac{{2}}{{9}}{{x}}^{{3}}\right)}{{\mid}_{{0}}^{{{10}}}}\approx{1.09}\times{{10}}^{{7}}\ {N}$.

Example 2. Find force due to hydrostatic pressure on circular plate of radius 4 that is 3 meters under water.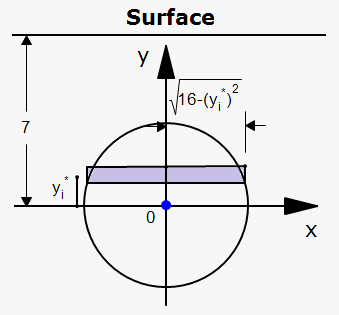

Again we need convention about ${x}$. This time we will take origin to be at the center of circle and ${x}$ pointing to the right (standard rectangular system).

Now we split plate by ${n}$ horizontal strips of heigth $\Delta{y}$ and choose sample point ${{y}_{{i}}^{\star}}$ from i-th strip.

We can approximate area of i-th strip by rectangle with height $\Delta{y}$ and width ${2}\sqrt{{{16}-{{\left({{y}_{{i}}^{\star}}\right)}}^{{2}}}}$: ${A}_{{i}}\approx{2}\sqrt{{{16}-{{\left({{y}_{{i}}^{\star}}\right)}}^{{2}}}}{d}{y}$.

i-strip is ${7}-{{y}_{{i}}^{\star}}$ meters under water the pressure on each strip is ${P}_{{i}}\approx\rho\cdot{g{\cdot}}{\left({7}-{{y}_{{i}}^{\star}}\right)}={9800}{\left({7}-{{y}_{{i}}^{\star}}\right)}$.

Now force that acts on each strip is ${F}_{{i}}\approx{P}_{{i}}{A}_{{i}}={19600}{\left({7}-{{y}_{{i}}^{\star}}\right)}\sqrt{{{16}-{{\left({{y}_{{i}}^{\star}}\right)}}^{{2}}}}{d}{y}$.

If we now add force that acts on each strip and take limit ${n}\to\infty$ then we will obtain that ${F}={19600}{\int_{{-{4}}}^{{4}}}{\left({7}-{y}\right)}\sqrt{{{16}-{{y}}^{{2}}}}{d}{y}={19600}{\left({\int_{{-{4}}}^{{4}}}{7}\sqrt{{{16}-{{y}}^{{2}}}}{d}{y}-{\int_{{-{4}}}^{{4}}}{y}\sqrt{{{16}-{{y}}^{{2}}}}\right)}{d}{y}$.

First interval requires trigonometric substitution ${y}={4}{\sin{{\left({u}\right)}}}$, second requires substitution ${v}={16}-{{y}}^{{2}}$.

So, ${F}={1097600}\pi$.