Rolle's Theorem

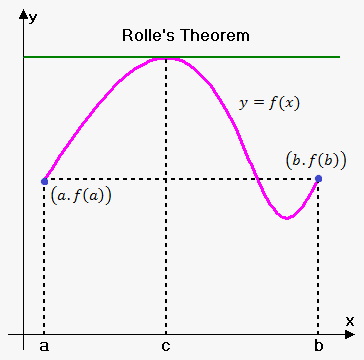Geometrically Rolle's theorem means the following: if $$${f{{\left({a}\right)}}}={f{{\left({b}\right)}}}$$$ then there exists point $$${c}$$$ at which tangent line is horizontal.

Note, that all three conditions are needed.

For function $$${f{{\left({x}\right)}}}={x}-{\left[{x}\right]}$$$ on interval $$${\left[{0},{1}\right]}$$$ first condition doesn't hold, because it is not continuous at $$${x}={1}$$$. And $$${f{'}}{\left({x}\right)}={1}$$$ on $$${\left({0},{1}\right)}$$$, so there are no point $$${c}$$$ from $$${\left({0},{1}\right)}$$$ such that $$${f{'}}{\left({c}\right)}={0}$$$.

For function $$${f{{\left({x}\right)}}}={\left\{\begin{array}{c}{x}{\quad\text{if}\quad}{0}\le{x}\le\frac{{1}}{{2}}\\{1}-{x}{\quad\text{if}\quad}\frac{{1}}{{2}}\le{x}\le{1}\\ \end{array}\right.}$$$ second condition doesn't hold, because derivative doesn't exist at $$${x}=\frac{{1}}{{2}}$$$. Aso $$${f{'}}{\left({x}\right)}={1}$$$ on $$${\left({0},\frac{{1}}{{2}}\right)}$$$ and $$${f{'}}{\left({x}\right)}=-{1}$$$ on $$${\left(\frac{{1}}{{2}},{1}\right)}$$$, so there are no point $$${c}$$$ from $$${\left({0},{1}\right)}$$$ such that $$${f{'}}{\left({c}\right)}={0}$$$.

For function $$${f{{\left({x}\right)}}}={x}$$$ on interval $$${\left[{0},{1}\right]}$$$ third condition doesn't hold, $$${f{{\left({0}\right)}}}\ne{f{{\left({1}\right)}}}$$$. And $$${f{'}}{\left({x}\right)}={1}$$$ everywhere, so there are no point $$${c}$$$ from $$${\left({0},{1}\right)}$$$ such that $$${f{'}}{\left({c}\right)}={0}$$$.