Mean Value Theorem

Mean Value Theorem (Lagrange Theorem). Suppose that function $y={f{{\left({x}\right)}}}$ is defined and continuous on closed interval ${\left[{a},{b}\right]}$ and exists finite derivative ${f{'}}{\left({x}\right)}$ on interval ${\left({a},{b}\right)}$ . Then there exists a point $c$ $\left({a}<{c}<{b}\right)$ such that $\frac{{{f{{\left({b}\right)}}}-{f{{\left({a}\right)}}}}}{{{b}-{a}}}={f{'}}{\left({c}\right)}$ .

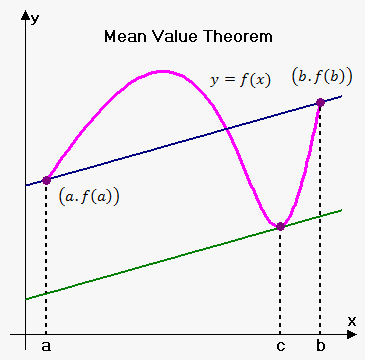mean value theorem Note, that there can be more than one such point.

Recall that $\frac{{{f{{\left({b}\right)}}}-{f{{\left({a}\right)}}}}}{{{b}-{a}}}$ is slope of line through points ${\left({a},{f{{\left({a}\right)}}}\right)}$ and ${\left({b},{f{{\left({b}\right)}}}\right)}$ .

So, a geometrical interpretation of the Mean Value Theorem is following: there exists such number $c$ between $a$ and $b$ that tangent line at this point is parallel to the line that passes through points ${\left({a},{f{{\left({a}\right)}}}\right)}$ and ${\left({b},{f{{\left({b}\right)}}}\right)}$ .

Example. If an object moves in a straight line with position function $s={f{{\left({t}\right)}}}$ , then the average velocity between $a$ and $b$ is $\frac{{{f{{\left({b}\right)}}}-{f{{\left({a}\right)}}}}}{{{b}-{a}}}$ and the velocity at $t=c$ is ${f{'}}{\left({c}\right)}$ . Thus, the Mean Value Theorem tells us that at some time ${t}={c}$ between ${a}$ and ${b}$ the instantaneous velocity is equal to that average velocity. For instance, if a car traveled 200 km in 2 hours, then the speedometer must have showed ${100}\frac{{{k}{m}}}{{h}}$ at least once.