Squeeze (Sandwich) Theorem for Sequences
Consider two sequences $$${x}_{{n}}$$$ and $$${y}_{{n}}$$$. When we write that $$${x}_{{n}}={y}_{{n}}$$$ we mean that corresponding values are equal, i.e. $$${x}_{{1}}={y}_{{1}}$$$, $$${x}_{{2}}={y}_{{2}}$$$ etc.
Fact 1. If two sequences $$${x}_{{n}}$$$ and $$${y}_{{n}}$$$ are equal: $$${x}_{{n}}={y}_{{n}}$$$, and each of them has limit (finite or infinite): $$$\lim{x}_{{n}}={a}$$$ and $$$\lim{y}_{{n}}={b}$$$ then $$${a}={b}$$$.
This fact is used in limiting process: from $$${x}_{{n}}={y}_{{n}}$$$ we conclude that $$$\lim{x}_{{n}}=\lim{y}_{{n}}$$$.
Fact 2. If for two sequences $$${x}_{{n}}$$$ and $$${y}_{{n}}$$$ we have that $$${x}_{{n}}\ge{y}_{{n}}$$$, and each of them has limit (finite or infinite): $$$\lim{x}_{{n}}={a}$$$ and $$$\lim{y}_{{n}}={b}$$$ then $$${a}\ge{b}$$$.
This fact is used in limiting process: from $$${x}_{{n}}\ge{y}_{{n}}$$$ we conclude that $$$\lim{x}_{{n}}\ge\lim{y}_{{n}}$$$.
Of course sign $$$\ge$$$ can be replaced by sign $$$\le$$$, i.e. from $$${x}_{{n}}\le{y}_{{n}}$$$ we conclude that $$$\lim{x}_{{n}}\le\lim{y}_{{n}}$$$.
CAUTION! Inequality $$${x}_{{n}}>{y}_{{n}}$$$ we can't conclude that $$$\lim{x}_{{n}}>\lim{y}_{{n}}$$$, we can only conclude that $$$\lim{x}_{{n}}\ge\lim{y}_{{n}}$$$.
For example, consider two sequences $$${x}_{{n}}=\frac{{1}}{{n}}$$$ and $$${y}_{{n}}=-\frac{{1}}{{n}}$$$. Clearly, $$${x}_{{n}}>{y}_{{n}}$$$ but $$$\lim\frac{{1}}{{n}}=\lim-\frac{{1}}{{n}}={0}$$$.
Fact 3 (Squeeze Theorem for Sequences). Consider three sequences $$${x}_{{n}},{y}_{{n}},{z}_{{n}}$$$. If we have that $$${x}_{{n}}\le{y}_{{n}}\le{z}_{{n}}$$$, and sequence $$${x}_{{n}}$$$ and $$${z}_{{n}}$$$ have same limit (finite or infinite), i.e. $$$\lim{x}_{{n}}=\lim{z}_{{n}}={a}$$$, then $$$\lim{y}_{{n}}={a}$$$.
This theorem tells us folowing: if there are three sequences, two of which have same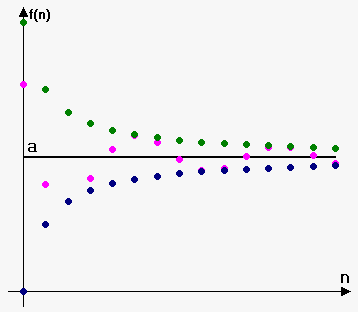 
limit and third is "squeezed" between them, then third will have same limit as first two.
Consider figure to the right. Let sequence drawn in green and sequence drawn in blue have same limit $$${a}$$$. Since sequence drawn in pink is "squeezed" between them, then it will also have limit $$${a}$$$.
From this theorem it follows that if for all $$${n}$$$ $$${a}\le{y}_{{n}}\le{z}_{{n}}$$$ and $$${z}_{{n}}\to{a}$$$ then $$${y}_{{n}}\to{a}$$$.