Sandwich Theorem

Fact. If ${f{{\left({x}\right)}}}\le{g{{\left({x}\right)}}}$ when ${x}$ is near ${a}$ (except possibly at ${a}$ ) then $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}\le\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}$ .

This fact means that if values of ${f{{\left({x}\right)}}}$ are not larger than values of ${g{{\left({x}\right)}}}$ near ${a}$ , then ${f{{\left({x}\right)}}}$ approaches not larger limit than ${g{{\left({x}\right)}}}$ as ${x}\to{a}$ .

Sandwich Theorem (or Squeeze Theorem). Consider three functions ${f{{\left({x}\right)}}},{g{{\left({x}\right)}}},{h}{\left({x}\right)}$ . If we have that ${f{{\left({x}\right)}}}\le{g{{\left({x}\right)}}}\le{h}{\left({x}\right)}$ , when ${x}$ near ${a}$ (except possibly at ${a}$ ) and $\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}=\lim_{{{x}\to{a}}}{h}{\left({x}\right)}={L}$ then $\lim_{{{x}\to{a}}}{g{{\left({x}\right)}}}={L}$ .

This theorem tells us folowing: if there are three functions, two of which have same
limit as ${x}$ approaches ${a}$ and third is "squeezed" between them, then third will have to approach same limit as ${x}$ approaches ${a}$ as first two.

Example. Find $\lim_{{{x}\to{0}}}{{x}}^{{2}}{\cos{{\left(\frac{{1}}{{x}}\right)}}}$ .

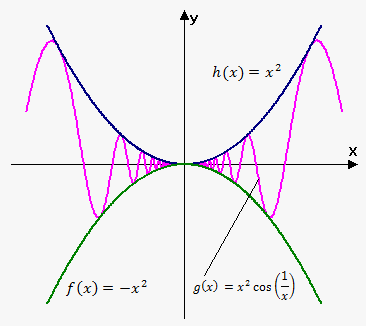squeeze theorem Since $-{1}\le{\cos{{\left(\frac{{1}}{{x}}\right)}}}\le{1}$ for all ${x}$ (actually we are interested only in ${x}$ near 0) then $-{{x}}^{{2}}\le{{x}}^{{2}}{\cos{{\left(\frac{{1}}{{x}}\right)}}}\le{{x}}^{{2}}$ . Since $\lim_{{{x}\to{0}}}{{x}}^{{2}}=\lim_{{{x}\to{0}}}-{{x}}^{{2}}={0}$ then by Squeeze theorem $\lim_{{{x}\to{0}}}{{x}}^{{2}}{\cos{{\left(\frac{{1}}{{x}}\right)}}}={0}$ .

On the figure you can see that ${{x}}^{{2}}{\cos{{\left(\frac{{1}}{{x}}\right)}}}$ is squeezed between ${{x}}^{{2}}$ and $-{{x}}^{{2}}$ .