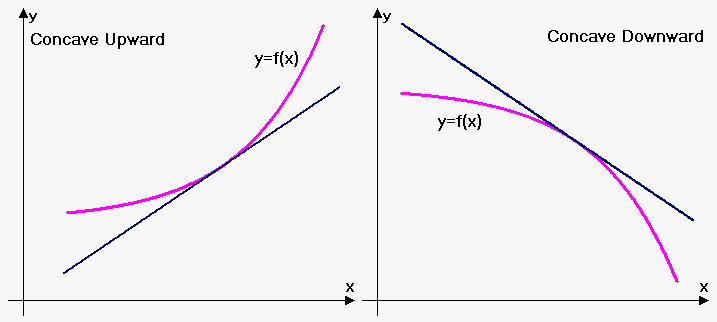
Conditions of Concavity (Convexity) of the Function
Often it is very hard to prove convexity (or concavity) of function through definition.
We need more powerful methods.
Fact 1. Suppose that function $$$y={f{{\left({x}\right)}}}$$$ is defined and continuous on interval $$${X}$$$, and has finite derivative $$${f{'}}{\left({x}\right)}$$$ inside it. Function $$$y={f{{\left({x}\right)}}}$$$ is concave upward (downward) on $$${X}$$$ if and only if derivative $$${f{'}}{\left({x}\right)}$$$ is non-decreasing (non-increasing). Function is strictly concave upward (downward) on $$${X}$$$ if and only if derivative $$${f{'}}{\left({x}\right)}$$$ is increasing (decreasing).
Geometrically this fact means the following: since derivative is slope of tangent line, then for concave upward function slopes of tangent line should increase and for concave downward function they should decrease.
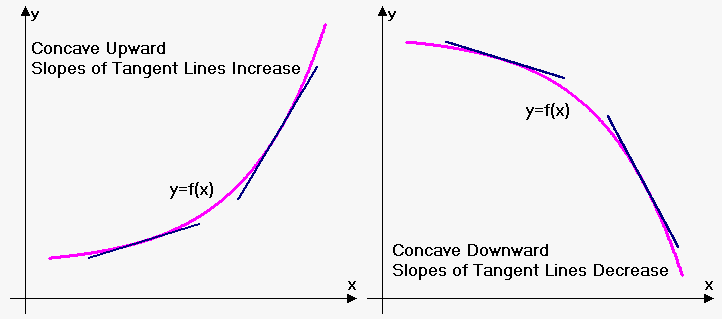On practice however, following fact is used, which is based on fact 1.
Fact 2. Suppose that function $$${y}={f{{\left({x}\right)}}}$$$ is defined and continuous together with its derivative $$${f{'}}{\left({x}\right)}$$$ on interval $$${X}$$$, and has finite second derivative $$${f{''}}{\left({x}\right)}$$$ inside it. Function $$${y}={f{{\left({x}\right)}}}$$$ is concave upward (downward) on $$${X}$$$ if and only if derivative $$${f{''}}{\left({x}\right)}\ge{0}$$$ $$$\left({f{''}}{\left({x}\right)}\le{0}\right)$$$. Function is strictly concave upward (downward) on $$${X}$$$ if and only if $$${f{''}}{\left({x}\right)}>{0}$$$ $$$\left({f{''}}{\left({x}\right)}<{0}\right)$$$.
Example 1. Function $$${y}={{x}}^{{2}}$$$ is strictly concave upward because $$${f{''}}{\left({x}\right)}={2}>{0}$$$ for all $$${x}$$$.
Example 2. Function $$${y}={{e}}^{{x}}$$$ is strictly concave upward because $$${f{''}}{\left({x}\right)}={{e}}^{{x}}>{0}$$$ for all $$${x}$$$.
Example 3. Function $$${y}={\ln{{\left({x}\right)}}}$$$ is strictly concave downward on $$${\left({0},\infty\right)}$$$ because $$${f{''}}{\left({x}\right)}=-\frac{{1}}{{{x}}^{{2}}}<{0}$$$ for all $$${x}$$$, but function is defined only for $$${x}>{0}$$$.
Example 4. Function $$${f{{\left({x}\right)}}}={x}{\ln{{\left({x}\right)}}}$$$ is concave upward because $$${f{'}}{\left({x}\right)}={\ln{{\left({x}\right)}}}+{1}$$$ and $$${f{''}}{\left({x}\right)}=\frac{{1}}{{x}}>{0}$$$ for $$${x}>{0}$$$ and function is defined for $$${x}>{0}$$$.
Example 5. Find where function $$${y}={{x}}^{{4}}-{4}{{x}}^{{3}}$$$ is concave upward and downward.
Let's find second derivative.
$$${f{'}}{\left({x}\right)}={4}{{x}}^{{3}}-{12}{{x}}^{{2}}$$$ and $$${f{''}}{\left({x}\right)}={12}{{x}}^{{2}}-{24}{x}={12}{x}{\left({x}-{2}\right)}$$$.
We use method of intervals to find where $$${f{''}}{\left({x}\right)}>{0}$$$ and where is $$${f{''}}{\left({x}\right)}<{0}$$$.
So $$${f{''}}{\left({x}\right)}={0}$$$ when $$${x}={0}$$$ and $$${x}={2}$$$.
These two values divide number line into three intervals:
First interval is $$${\left(-\infty,{0}\right)}$$$: here $$${x}<{0}$$$ and $$${x}-{2}<{0}$$$ so $$${f{''}}{\left({x}\right)}>{0}$$$.
Second interval is $$${\left({0},{2}\right)}$$$: here $$${x}>{0}$$$ and $$${x}-{2}<{0}$$$ so $$${f{''}}{\left({x}\right)}<{0}$$$.
Third interval is $$${\left({2},\infty\right)}$$$: here $$${x}>{0}$$$ and $$${x}-{2}>{0}$$$ so $$${f{''}}{\left({x}\right)}>{0}$$$.
Thus, function is concave upward on $$${\left(-\infty,{0}\right)}\cup{\left({2},\infty\right)}$$$ and concave downward on $$${\left({0},{2}\right)}$$$.
Example 6. Discuss concavity of the function $$${f{{\left({x}\right)}}}={{x}}^{{2}}{{e}}^{{-{x}}}$$$.
Let's find second derivative.
$$${f{'}}{\left({x}\right)}={2}{x}{{e}}^{{-{x}}}-{{x}}^{{2}}{{e}}^{{-{x}}}$$$ and $$${f{''}}{\left({x}\right)}={2}{{e}}^{{-{x}}}-{2}{x}{{e}}^{{-{x}}}-{2}{x}{{e}}^{{-{x}}}+{{x}}^{{2}}{{e}}^{{-{x}}}={{e}}^{{-{x}}}{\left({{x}}^{{2}}-{4}{x}+{2}\right)}$$$.
Since $$${{e}}^{{-{x}}}>{0}$$$ for all $$${x}$$$ then it doesn't influence sign of derivative, so we ignore it.
To find where $$${\left({{x}}^{{2}}-{4}{x}+{2}\right)}={\left({x}-{2}-\sqrt{{{2}}}\right)}{\left({x}-{2}+\sqrt{{{2}}}\right)}$$$ is positive and where it is negative we use method of intervals.
So $$${f{''}}{\left({x}\right)}={0}$$$ when $$${x}={2}-\sqrt{{{2}}}$$$ and $$${x}={2}+\sqrt{{{2}}}$$$.
These two values divide number line into three intervals:
First interval is $$${\left(-\infty,{2}-\sqrt{{{2}}}\right)}$$$: here $$${x}-{2}-\sqrt{{{2}}}<{0}$$$ and $$${x}-{2}+\sqrt{{{2}}}<{0}$$$ so $$${f{''}}{\left({x}\right)}>{0}$$$.
Second interval is $$${\left({2}-\sqrt{{{2}}},{2}+\sqrt{{{2}}}\right)}$$$: here $$${x}-{2}-\sqrt{{{2}}}<{0}$$$ and $$${x}-{2}+\sqrt{{{2}}}>{0}$$$ so $$${f{''}}{\left({x}\right)}<{0}$$$.
Third interval is $$${\left({2}+\sqrt{{{2}}},\infty\right)}$$$: here $$${x}-{2}-\sqrt{{{2}}}>{0}$$$ and $$${x}-{2}+\sqrt{{{2}}}>{0}$$$ so $$${f{''}}{\left({x}\right)}>{0}$$$.
Thus, function is concave upward on $$${\left(-\infty,{2}-\sqrt{{{2}}}\right)}\cup{\left({2}+\sqrt{{{2}}},\infty\right)}$$$ and concave downward on $$${\left({2}-\sqrt{{{2}}},{2}+\sqrt{{{2}}}\right)}$$$.
At last let's formulate another geometric property of concave upward function.
Fact 3. Suppose function $$${y}={f{{\left({x}\right)}}}$$$ is defined and continuous on interval $$${X}$$$ and has finite derivative $$${f{'}}{\left({x}\right)}$$$ inside it. Function $$${y}={f{{\left({x}\right)}}}$$$ is concave upward (downward) if all values of function on interval $$${X}$$$ lie above (below) any tangent line (or on it).
