Commutative Property of Multiplication
Commutative property of multiplication:
$$$\color{purple}{a\times b=b\times a}$$$
 What does it mean?
What does it mean?
It means, that order of numbers doesn't matter.
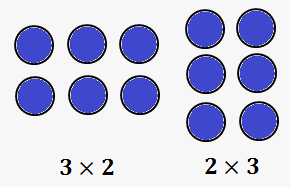
Indeed, as can be seen from illustration, we can count there are 3 circles in a row, and there are 2 rows, so total number of squares is $$${3}\times{2}={6}$$$.
From another side, we can rotate picture and count circles in another way: 3 rows, and in each row 2 circles: $$${2}\times{3}={6}$$$.
Warning: it doesn't work with division, i.e. $$$\frac{{a}}{{b}}\ne\frac{{b}}{{a}}$$$.
For example, $$$\frac{{3}}{{2}}\ne\frac{{2}}{{3}}$$$.
However, commutative property of multiplication works for negative numbers (in fact, for real numbers) as well.
Example 1. $$${3}\times{\left(-{4}\right)}={\left(-{4}\right)}\times{3}=-{12}$$$.
Example 2. $$${\left(-{2.51}\right)}\times{\left(-{3.4}\right)}={\left(-{3.4}\right)}\times{\left(-{2.51}\right)}$$$.
Example 3. $$$-\frac{{5}}{{8}}\times\frac{{2}}{{3}}={\left(-\frac{{5}}{{8}}\right)}\times\frac{{2}}{{3}}=-\frac{{5}}{{12}}$$$.
Conclusion. So, the basic rule here is following: whenever you see multiplication, you can interchange factors.
