Square of Sum and Difference

Square of sum and difference:

$\color{purple}{\left(a\pm b\right)^2=a^2\pm 2ab+b^2}$

Let's see how to derive it.

Recall, that exponent is just repeating multiplication.

Thus, we can write that ${{\left({a}+{b}\right)}}^{{2}}={\left({a}+{b}\right)}{\left({a}+{b}\right)}$ .

Now, apply FOIL: ${\left({a}+{b}\right)}{\left({a}+{b}\right)}={a}\cdot{a}+{a}\cdot{b}+{b}\cdot{a}+{b}\cdot{b}={{a}}^{{2}}+{2}{a}{b}+{{b}}^{{2}}$ .

square of sum and difference Similarly, it can be shown, that ${{\left({a}-{b}\right)}}^{{2}}={{a}}^{{2}}-{2}{a}{b}+{{b}}^{{2}}$ .

Or, more shortly: ${{\left({a}\pm{b}\right)}}^{{2}}={{a}}^{{2}}\pm{2}{a}{b}+{{b}}^{{2}}$ .

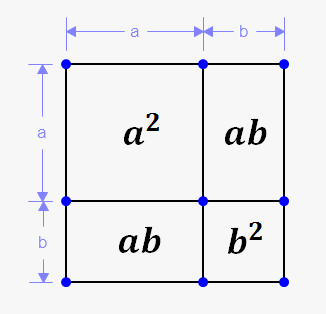
Geometrically ${{\left({a}+{b}\right)}}^{{2}}$ represents an area of the square with side ${a}+{b}$ .

But, as shown on picture, this square consist of four smaller squares with areas ${{a}}^{{2}}$ , ${a}{b}$ , ${a}{b}$ , ${{b}}^{{2}}$ .

Thus, ${{\left({a}+{b}\right)}}^{{2}}={{a}}^{{2}}+{a}{b}+{a}{b}+{{b}}^{{2}}={{a}}^{{2}}+{2}{a}{b}+{{b}}^{{2}}$ .

Example 1. Multiply ${{\left({2}{x}+{3}{y}\right)}}^{{2}}$ .

Here ${a}={2}{x}$ and ${b}={3}{y}$ .

Just use above formula: ${{\left({2}{x}+{3}{y}\right)}}^{{2}}={{\left({2}{x}\right)}}^{{2}}+{2}\cdot{\left({2}{x}\right)}\cdot{\left({3}{y}\right)}+{{\left({3}{y}\right)}}^{{2}}={4}{{x}}^{{2}}+{12}{x}{y}+{9}{{y}}^{{2}}$ .

Let's see how to handle minus sign.

Example 2. Multiply ${{\left(\frac{{8}}{{3}}{a}{b}-{3}{c}{d}\right)}}^{{2}}$ .

Here ${a}=\frac{{8}}{{3}}{a}{b}$ and ${b}={3}{c}{d}$ .

Now, use formula for difference: ${{\left(\frac{{8}}{{3}}{a}{b}-{3}{c}{d}\right)}}^{{2}}={{\left(\frac{{8}}{{3}}{a}{b}\right)}}^{{2}}-{2}\cdot{\left(\frac{{8}}{{3}}{a}{b}\right)}\cdot{\left({3}{c}{d}\right)}+{{\left({3}{c}{d}\right)}}^{{2}}=\frac{{64}}{{9}}{{a}}^{{2}}{{b}}^{{2}}-{16}{a}{b}{c}{d}+{9}{{c}}^{{2}}{{d}}^{{2}}$ .

Finally, let's do a slightly harder example.

Example 3. Multiply the following: ${{\left(-{x}{y}{z}-{5}{{x}}^{{2}}\right)}}^{{2}}$ .

Till now, we didn't see two minus signs, but this case can be handled easily.

There are two options:

${a}=-{x}{y}{z}$ and ${b}=-{5}{{x}}^{{2}}$ ; apply sum formula.
${a}=-{x}{y}{z}$ and ${b}={5}{{x}}^{{2}}$ ; apply difference formula.

I choose second option: ${{\left(-{x}{y}{z}-{5}{{x}}^{{2}}\right)}}^{{2}}={{\left(-{x}{y}{z}\right)}}^{{2}}-{2}\cdot{\left(-{x}{y}{z}\right)}\cdot{\left({5}{{x}}^{{2}}\right)}+{{\left({5}{{x}}^{{2}}\right)}}^{{2}}={{x}}^{{2}}{{y}}^{{2}}{{z}}^{{2}}+{10}{{x}}^{{3}}{y}{z}+{25}{{x}}^{{4}}$ .

From last example we see, that ${\color{purple}{{{{\left(-{a}-{b}\right)}}^{{2}}={{\left({a}+{b}\right)}}^{{2}}}}}$ .

Another nice application of square of sum formula is to calculate square of a number. In many cases you can perform calculations mentally without calculator (or pen and paper).

Example 4. Calculate ${{24}}^{{2}}$ .

We could use calculator or multiply vertically, but there is simpler way.

We know, that ${{20}}^{{2}}={400}$ .

Thus, ${{24}}^{{2}}={{\left({20}+{4}\right)}}^{{2}}={{20}}^{{2}}+{2}\cdot{20}\cdot{4}+{{4}}^{{2}}={400}+{160}+{16}={576}$ .

Alternatively ${{24}}^{{2}}={{\left({30}-{6}\right)}}^{{2}}={{30}}^{{2}}-{2}\cdot{30}\cdot{6}+{{6}}^{{2}}={900}-{360}+{36}={576}$ .

Note, that this method is not always the simplest.

Now, it is time to exercise.

Exercise 1. Multiply ${{\left({5}{z}+{3}{y}\right)}}^{{2}}$ .

Answer: ${25}{{z}}^{{2}}+{30}{z}{y}+{9}{{y}}^{{2}}$ .

Exercise 2. Multiply ${{\left(-\frac{{1}}{{3}}{x}{{y}}^{{2}}+{2}{x}\right)}}^{{2}}$ .

Answer: $\frac{{1}}{{9}}{{x}}^{{2}}{{y}}^{{4}}-\frac{{4}}{{3}}{{x}}^{{2}}{{y}}^{{2}}+{4}{{x}}^{{2}}$ .

Hint: either swap summands ( ${{\left(-\frac{{1}}{{3}}{x}{{y}}^{{2}}+{2}{x}\right)}}^{{2}}={{\left({2}{x}-\frac{{1}}{{3}}{x}{{y}}^{{2}}\right)}}^{{2}}$ : commutative property of addition) or proceed as always.

Exercise 3. Multiply the following: ${{\left(-{3}{x}-{2}\right)}}^{{2}}$ .

Answer: ${9}{{x}}^{{2}}+{12}{x}+{4}$ .

Exercise 4. Calculate ${{31}}^{{2}}$ using square of sum/difference formula.

Answer: ${961}$ . Hint: ${{31}}^{{2}}={{\left({30}+{1}\right)}}^{{2}}$ or ${{31}}^{{2}}={{\left({40}-{9}\right)}}^{{2}}$ (however, first option is easier).