Adding Polynomials

To add polynomials we need to combine (add) like terms using distributive property of multiplication.

Recall, that like terms are terms that contain same variables, raised to the same powers. In other words, like terms are "like" each other. For example, ${5}{{x}}^{{3}}{{y}}^{{2}}$ and ${2}{{x}}^{{3}}{{y}}^{{2}}$ .

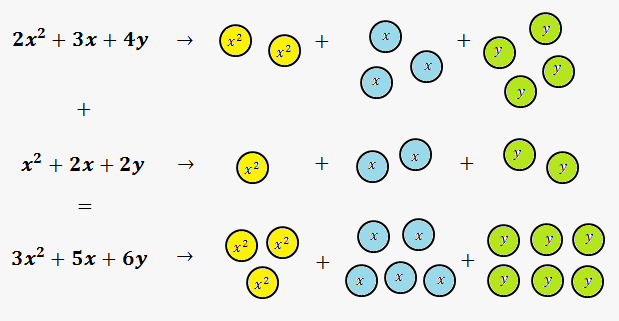adding polynomials Graphically we can represent like terms in the form of some figures. Then addition of terms means addition of similar figures. In the figure to the right like terms are represented by circles with different color.

Note, that we can add polynomials either horizontally or vertically.

Example 1. Simplify ${\left({5}{x}+{2}{y}\right)}+{\left({3}{x}+{7}{y}\right)}$ (parenthesis are written to separate polynomials).

Horizontally.

We rewrite expression, using commutative property of addition, in the following way: ${5}{x}+{2}{y}+{3}{x}+{7}{y}={5}{x}+{3}{x}+{2}{y}+{7}{y}$ .

Now, just use distributive property of multiplication: ${5}{x}+{3}{x}+{2}{y}+{7}{y}={\left({5}+{3}\right)}{x}+{\left({2}+{7}\right)}{y}={8}{x}+{9}{y}$ .

Vertically.

$\begin{array}{r} \ & 5\color{blue}{x}&+&2\color{green}{y} \\+ & 3\color{blue}{x}&+&7\color{green}{y} \\ \hline & 8\color{blue}{x}&+&9\color{green}{y} \\ \end{array}$

Thus, ${\left({5}{x}+{2}{y}\right)}+{\left({3}{x}+{7}{y}\right)}={8}{x}+{9}{y}$ .

Sometimes, there are some terms in one polynomial, that can be absent in another. In this case, for vertical addition, you need to correctly line up polynomials and leave gaps, where needed.

Also, terms in polynomials can be written in different order. When adding vertically, write like terms one under another.

Example 2. Simplify ${\left({3}{{x}}^{{4}}+{{x}}^{{3}}+{1}\right)}+{\left({2}{{x}}^{{4}}-{5}-{7}{{x}}^{{2}}\right)}$ .

Horizontally.

${3}{{x}}^{{4}}+{{x}}^{{3}}+{1}+{2}{{x}}^{{4}}-{5}-{7}{{x}}^{{2}}={3}{{x}}^{{4}}+{2}{{x}}^{{4}}+{{x}}^{{3}}-{7}{{x}}^{{2}}+{1}-{5}={5}{{x}}^{{4}}+{{x}}^{{3}}-{7}{{x}}^{{2}}-{4}$ .

Vertically.

Remember to line up correctly.

$\begin{array}{r} \ & 3x^4&+&x^3&\phantom{+}&\phantom{7x^2}&+&1 \\ + &2x^4&\phantom{+}&\phantom{x^3}&-&7x^2&-&5 \\ \hline & 5x^4&+&x^3&-&7x^2&-&4 \\ \end{array}$

Thus, ${\left({3}{{x}}^{{4}}+{{x}}^{{3}}+{1}\right)}+{\left({2}{{x}}^{{4}}-{5}-{7}{{x}}^{{2}}\right)}={5}{{x}}^{{4}}+{{x}}^{{3}}-{7}{{x}}^{{2}}-{4}$ .

Finally, you can add more than 2 polynomials.

Example 3. Perform addition: ${\left({2}{{x}}^{{2}}-{3}{x}{y}+{5}{{y}}^{{2}}-{4}\right)}+{\left({7}{{x}}^{{2}}+{x}{y}-{3}\right)}+{\left({2}{x}{y}-{12}{{y}}^{{2}}+{{x}}^{{2}}-{7}\right)}$ .

Horizontally.

${2}{{x}}^{{2}}-{3}{x}{y}+{5}{{y}}^{{2}}-{4}+{7}{{x}}^{{2}}+{x}{y}-{3}+{2}{x}{y}-{12}{{y}}^{{2}}+{{x}}^{{2}}-{7}=$

$={2}{{x}}^{{2}}+{7}{{x}}^{{2}}+{{x}}^{{2}}-{3}{x}{y}+{x}{y}+{2}{x}{y}+{5}{{y}}^{{2}}-{12}{{y}}^{{2}}-{4}-{3}-{7}=$

$={\left({2}+{7}+{1}\right)}{{x}}^{{2}}+{\left(-{3}+{1}+{2}\right)}{x}{y}+{\left({5}-{12}\right)}{{y}}^{{2}}-{14}={10}{{x}}^{{2}}+{0}\cdot{x}{y}-{7}{{y}}^{{2}}-{14}=$

$={10}{{x}}^{{2}}-{7}{{y}}^{{2}}-{14}$ .

Vertically. Don't forget to write like terms under each other and fill gaps, where necessary.

$\begin{array}{r} \ & 2x^2&-&3xy&+&5y^2&-&4 \\ \ & 7x^2&+&xy&\phantom{+}&\phantom{5y^2}&-&3 \\+ &x^2&+&2xy&-&12y^2&-&7 \\ \hline & 10x^2&\phantom{+}&\phantom{3xy}&-&7y^2&-&14 \\ \end{array}$

Answer: ${\left({2}{{x}}^{{2}}-{3}{x}{y}+{5}{{y}}^{{2}}-{4}\right)}+{\left({7}{{x}}^{{2}}+{x}{y}-{3}\right)}+{\left({2}{x}{y}-{12}{{y}}^{{2}}+{{x}}^{{2}}-{7}\right)}={10}{{x}}^{{2}}-{7}{{y}}^{{2}}-{14}$ .

Now, it is time to exercise.

Exercise 1. Simplify ${\left({{x}}^{{2}}+{2}{x}{y}+{3}{{y}}^{{2}}\right)}+{\left({2}{{y}}^{{2}}+{3}{{x}}^{{2}}-{5}{x}{y}\right)}$ .

Answer: ${4}{{x}}^{{2}}-{3}{x}{y}+{5}{{y}}^{{2}}$ .

Exercise 2. Perform addition: ${\left(-{1}+{2}{{x}}^{{3}}\right)}+{\left({{x}}^{{2}}+{4}-{5}{{x}}^{{3}}\right)}$ .

Answer: $-{3}{{x}}^{{3}}+{{x}}^{{2}}+{3}$ .

Exercise 3. Simplify ${\left({x}{{y}}^{{2}}-{2}{{x}}^{{2}}{{y}}^{{2}}+{3}{{x}}^{{3}}\right)}+{\left({2}{{x}}^{{2}}{{y}}^{{2}}-{5}{{x}}^{{3}}-{7}{{x}}^{{2}}{y}\right)}+{\left({2}{{x}}^{{3}}-{4}{{x}}^{{2}}{{y}}^{{2}}\right)}$ .

Answer: $-{4}{{x}}^{{2}}{{y}}^{{2}}-{7}{{x}}^{{2}}{y}+{x}{{y}}^{{2}}$ .