Inverse of a Function
We already know that a function is a rule that allows finding for every value of $$${x}$$$ the corresponding value of $$${y}$$$. But what if we are given a rule, i.e. a function, and the value of $$${y}$$$ and we want to find the corresponding value of $$${x}$$$?
In other words, we want to find a function that will express $$${x}$$$ in terms of $$${y}$$$. Such a function is called an inverse function and is denoted by $$${{f}}^{{-{1}}}$$$.
If $$${y}={f{{\left({x}\right)}}}$$$, the inverse function is $$${x}={{f}}^{{-{1}}}{\left({y}\right)}$$$.
For example, if $$${y}={f{{\left({x}\right)}}}={{x}}^{{3}}$$$, it can be stated that $$${{f}}^{{-{1}}}{\left({27}\right)}={3}$$$, because $$${f{{\left({3}\right)}}}={27}$$$.
Not all functions have a unique inverse. Let's take the function $$${f{{\left({x}\right)}}}={{x}}^{{2}}$$$. Since $$${f{{\left(-{2}\right)}}}={4}$$$ and $$${f{{\left({2}\right)}}}={4}$$$, it can be concluded that $$${{f}}^{{-{1}}}{\left({4}\right)}$$$ is undefined, because there are 2 values that correspond to $$${4}$$$, namely $$${2}$$$ and $$$-{2}$$$. Therefore, the inverse of $$${y}={{x}}^{{2}}$$$ is a multi-valued function. In this case, we will say that the function doesn't have an inverse, because the inverse is a multi-valued function, which we don't consider to be a function.
So, a function will have an inverse only when for different values of $$${x}$$$ we have different values of $$${y}$$$.
Definition: a function $$${f{}}$$$ is called one-to-one (or injective), if it never takes the same value twice, i.e. $$${f{{\left({x}_{{1}}\right)}}}\ne{f{{\left({x}_{{2}}\right)}}}$$$ whenever $$${x}_{{1}}\ne{x}_{{2}}$$$.
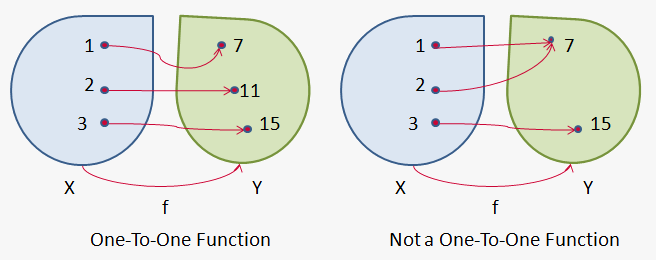
One-to-one functions are precisely the functions that possess inverse functions.
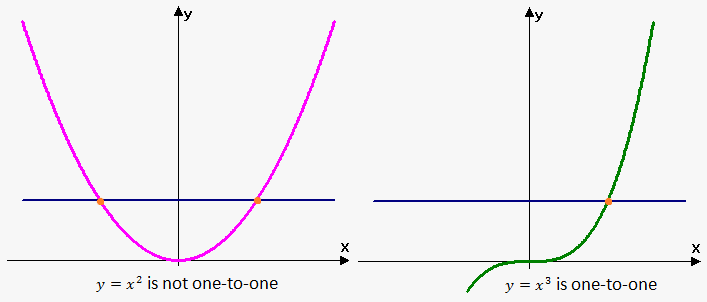
From this definition, it follows that $$${y}={{x}}^{{2}}$$$ is not a one-to-one function, because $$${y}{\left({2}\right)}={y}{\left(-{2}\right)}={4}$$$; so, different values have the same output.
On the other hand, $$${y}={{x}}^{{3}}$$$ is a one-to-one function, because $$${{x}_{{1}}^{{3}}}\ne{{x}_{{2}}^{{3}}}$$$ whenever $$${x}_{{1}}\ne{x}_{{2}}$$$ (different values can't have the same cube). Thus, $$${y}={{x}}^{{3}}$$$ has an inverse.
Graphically, we can determine whether a function is one-to-one using the horizontal line test.
Horizontal line test. A function is one-to-one if and only if no horizontal line intersects its graph more than once.
Now, let's give a more formal definition of the inverse function.
Definition. Let $$${f{}}$$$ be a one-to-one function with the domain $$${X}$$$ and the range $$${Y}$$$. Then, its inverse function $$${{f}}^{{-{1}}}$$$ has the domain $$${Y}$$$ and the range $$${X}$$$ and is defined as follows: $$${{f}}^{{-{1}}}{\left({y}\right)}={x}\ \Leftrightarrow\ {f{{\left({x}\right)}}}={y}$$$.
Note that the domain of $$${f{}}$$$ equals the range of $$${{f}}^{{-{1}}}$$$ and the range of $$${f{}}$$$ equals the domain of $$${{f}}^{{-{1}}}$$$.
When we want to concentrate on the inverse function, we will usually write $$${y}={{f}}^{{-{1}}}{\left({x}\right)}$$$, i.e. we will interchange $$${x}$$$ and $$${y}$$$, because we traditionally use $$${x}$$$ as an independent variable.
The inverse function means that if we apply $$${f{}}$$$ to $$${x}$$$, we will obtain $$${y}$$$.
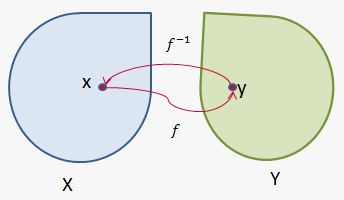
If we now apply $$${{f}}^{{-{1}}}$$$ to $$${y}$$$, we will arrive back at $$${x}$$$. And vice versa: applying $$${{f}}^{{-{1}}}$$$ to $$${y}$$$ and then applying $$${f{}}$$$ to the result will bring us back to $$${y}$$$.
As a result, we can say that a function and its inverse cancel the influence of each other.
Thus, there are two properties of inverse functions:
- $$${{f}}^{{-{1}}}{\left({f{{\left({x}\right)}}}\right)}={x}$$$ for any $$${x}$$$ from $$${X}$$$.
- $$${f{{\left({{f}}^{{-{1}}}{\left({x}\right)}\right)}}}={x}$$$ for any $$${x}$$$ from $$${Y}$$$.
Example 1. Given $$${f{{\left({1}\right)}}}={4}$$$, $$${f{{\left({2}\right)}}}={3}$$$, $$${f{{\left({5}\right)}}}={10}$$$, find $$${{f}}^{{-{1}}}{\left({3}\right)}$$$, $$${{f}}^{{-{1}}}{\left({4}\right)}$$$, $$${{f}}^{{-{1}}}{\left({5}\right)}$$$.
$$${{f}}^{{-{1}}}{\left({3}\right)}={2}$$$, because $$${f{{\left({2}\right)}}}={3}$$$.
$$${{f}}^{{-{1}}}{\left({4}\right)}={1}$$$, because $$${f{{\left({1}\right)}}}={4}$$$.
$$${{f}}^{{-{1}}}{\left({5}\right)}$$$ is undefined, because we are not given the value of $$${x}$$$ for which $$${f{{\left({x}\right)}}}={5}$$$.
Now, let’s see how to compute inverse functions. Since we have $$${y}={f{{\left({x}\right)}}}$$$, we need to express $$${x}$$$ in terms of $$${y}$$$ to obtain $$${{f}}^{{-{1}}}$$$.
Steps for finding an inverse:
- Write $$${y}={f{{\left({x}\right)}}}$$$.
- Express $$${x}$$$ in terms of $$${y}$$$ (if possible). You will get $$${x}={{f}}^{{-{1}}}{\left({y}\right)}$$$.
- To obtain $$${y}={{f}}^{{-{1}}}{\left({x}\right)}$$$, interchange $$${x}$$$ and $$${y}$$$.
Actually, we can first perform step 3 and then step 2, i.e. interchange $$${x}$$$ and $$${y}$$$, and then express $$${y}$$$ in terms of $$${x}$$$.
Example 2. Find the inverse of $$${y}={{x}}^{{3}}-{3}$$$.
- $$${y}={{x}}^{{3}}-{3}$$$.
- $$${x}={\sqrt[{{3}}]{{{y}+{3}}}}$$$.
- $$${y}={\sqrt[{{3}}]{{{x}+{3}}}}$$$ is the inverse.
Let's work another short example.
Example 3. Find the inverse of $$${y}=\frac{{{x}+{3}}}{{{2}{x}-{5}}}$$$.
- $$${y}=\frac{{{x}+{3}}}{{{2}{x}-{5}}}$$$.
- $$${2}{x}{y}-{5}{y}={x}+{3}$$$, or $$${x}=\frac{{{5}{y}+{3}}}{{{2}{y}-{1}}}$$$.
- $$${y}=\frac{{{5}{x}+{3}}}{{{2}{x}-{1}}}$$$ is the inverse.
To verify whether we found the inverse correctly, check if $$${f{{\left({{f}}^{{-{1}}}{\left({x}\right)}\right)}}}={x}$$$ holds.
Here, $$${f{{\left({x}\right)}}}=\frac{{{x}+{3}}}{{{2}{x}-{5}}}$$$, and $$${{f}}^{{-{1}}}{\left({x}\right)}=\frac{{{5}{x}+{3}}}{{{2}{x}-{1}}}$$$; so, $$${f{{\left({{f}}^{{-{1}}}{\left({x}\right)}\right)}}}=\frac{{\frac{{{5}{x}+{3}}}{{{2}{x}-{1}}}+{3}}}{{{2}\frac{{{5}{x}+{3}}}{{{2}{x}-{1}}}-{5}}}={x}$$$.
Thus, we found the inverse correctly.
Interchanging the roles of $$${x}$$$ and $$${y}$$$ gives the opportunity to plot the graph of the inverse function based on the graph of the function $$${y}={f{{\left({x}\right)}}}$$$. Since the point $$${\left({x}_{{0}},{y}_{{0}}\right)}$$$ lies on the graph of $$${f{}}$$$, we have that $$${\left({y}_{{0}},{x}_{{0}}\right)}$$$ lies on the graph of $$${{f}}^{{-{1}}}$$$. So, the graph of the inverse is obtained by reflecting the graph of the function about the line $$${y}={x}$$$.
Example 4. Sketch the graph of $$${y}=\sqrt{{{x}-{1}}}$$$ and its inverse.
The domain of $$${y}=\sqrt{{{x}-{1}}}$$$ is $$${x}-{1}\ge{0}$$$, or $$${x}\ge{1}$$$. The range is $$${y}\ge{0}$$$.
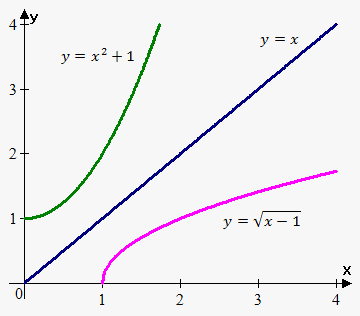
This means that the domain of the inverse is $$${x}\ge{0}$$$ and the range is $$${y}\ge{1}$$$.
To find the equation of the inverse, we write $$${x}$$$ in terms of $$${y}$$$: $$${{y}}^{{2}}={x}-{1}$$$, or $$${x}={{y}}^{{2}}+{1}$$$. Now, interchange $$${y}$$$ and $$${x}$$$: $$${y}={{x}}^{{2}}+{1}$$$.
So, the inverse is $$${y}={{x}}^{{2}}+{1}$$$.
Now, we draw the graph of the function $$${y}=\sqrt{{{x}-{1}}}$$$ on the interval $$${\left[{1},\infty\right)}$$$ and then reflect it about the line $$${y}={x}$$$.
